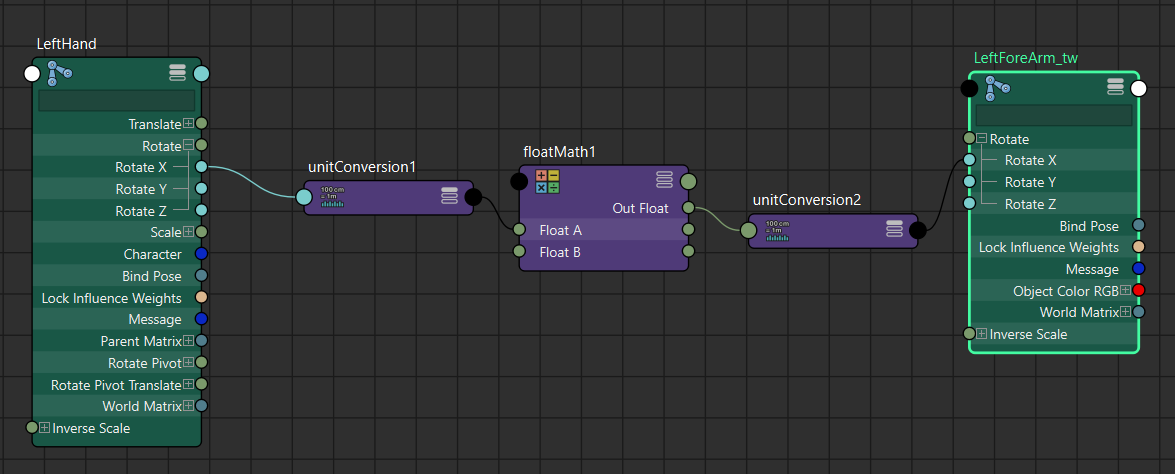
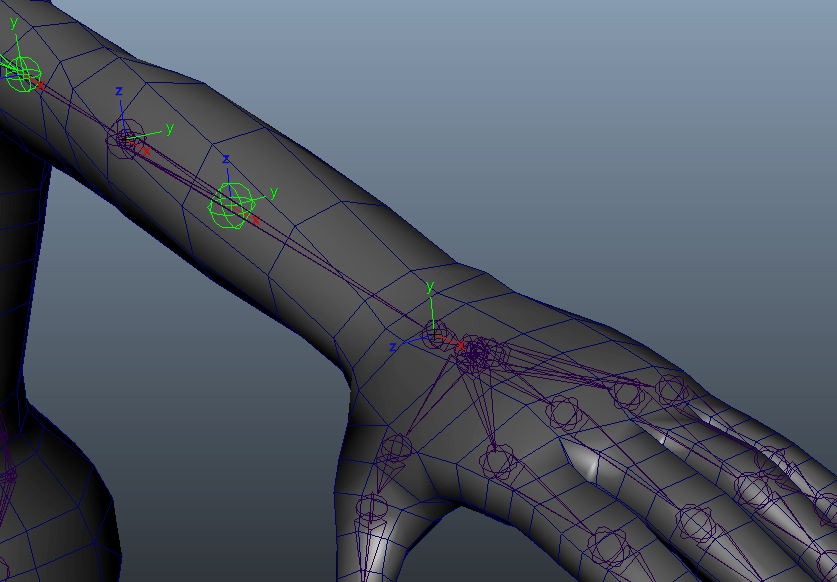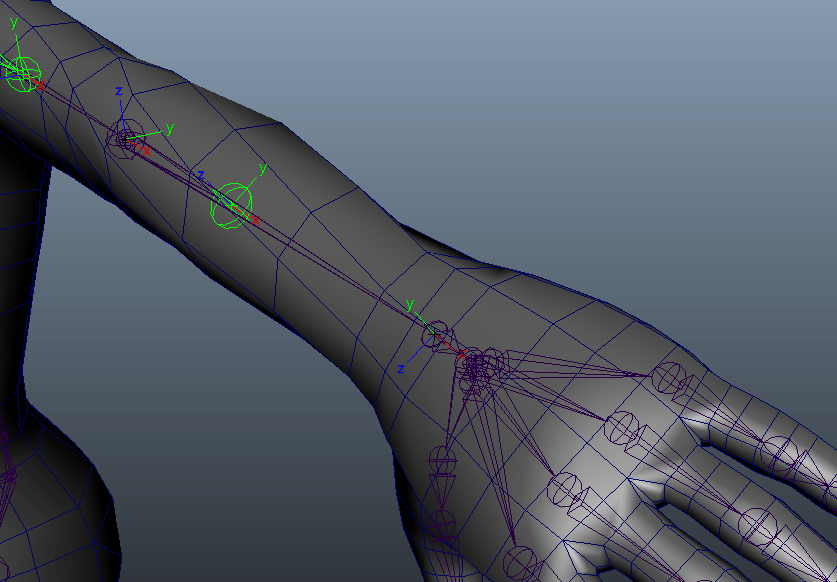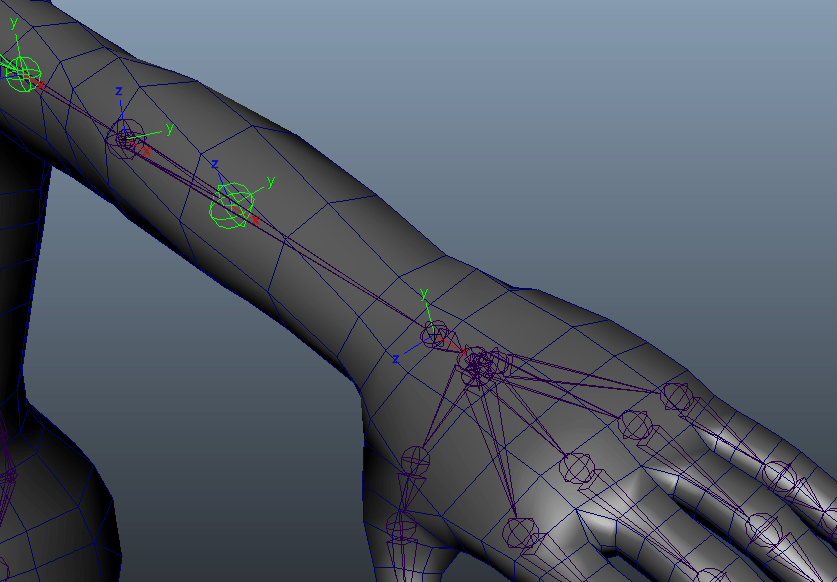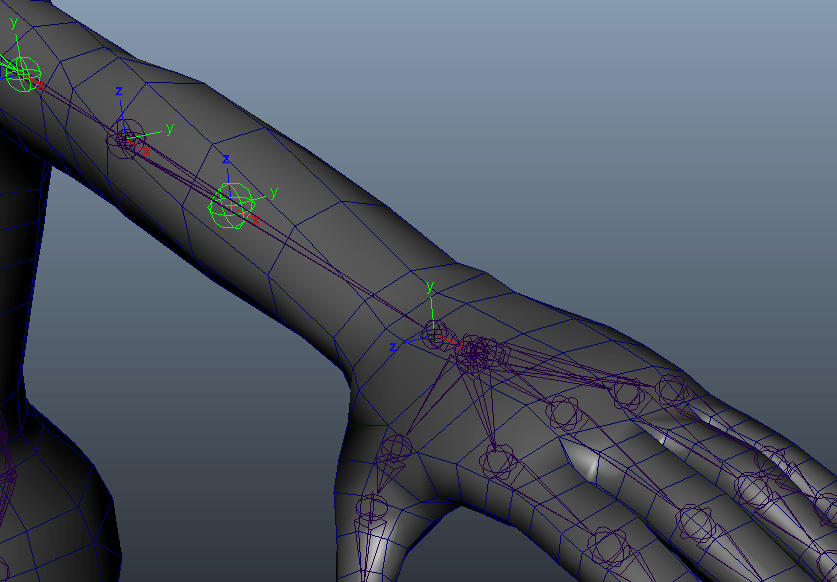
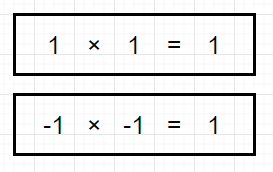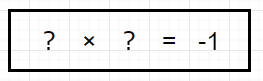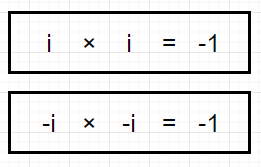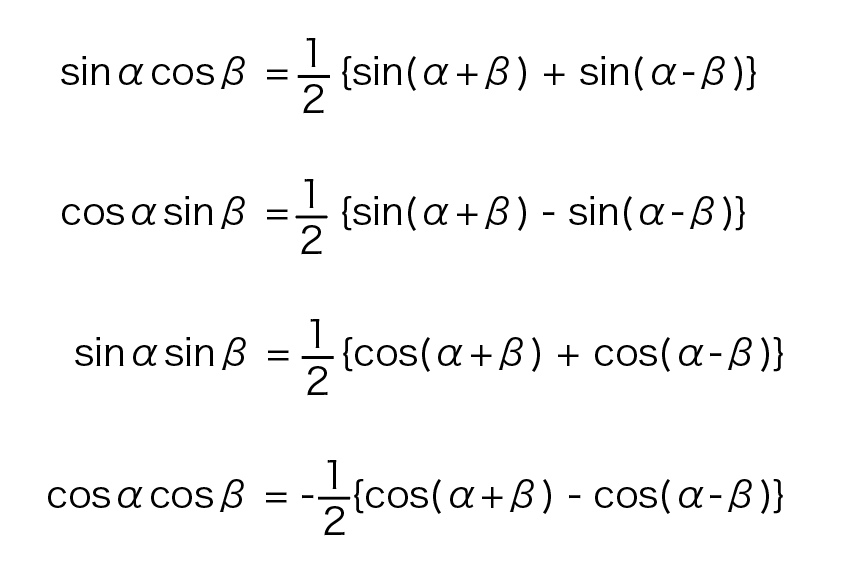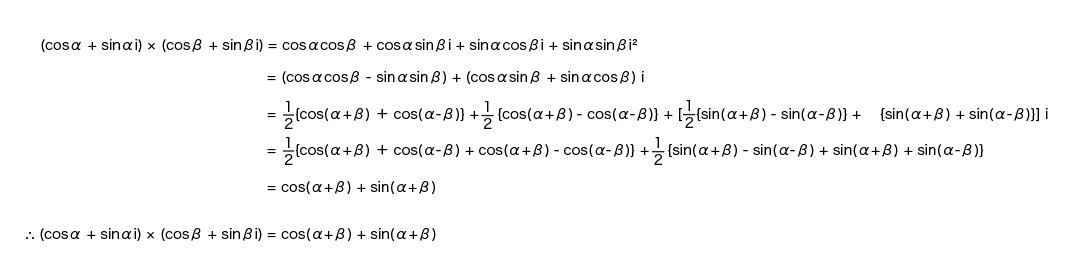クリーク・アンド・リバー社の社内CGスタジオであり、ゲームの3DCGグラフィックス制作を中心に手がけているCOYOTE 3DCG STUDIO。本連載では、同社のTAチームによる制作に役立つ技術TIPSを紹介していく。
TEXT_山本智人 / Tomohito Yamamoto(COYOTE 3DCG STUDIO)
EDIT_小村仁美 / Hitomi Komura(CGWORLD)
はじめに
おはこんばんちわ。COYOTE 3DCG STUDIO テクニカルアーティスト(以下、TA)の山本です。
全3回に渡って紹介するテクニカルTIPS「ノードの回転制御」、今回はその第2回です。
・ベクトルを使ったノードのBend制御(前回)
・Quaternionを使ったRoll成分の分解(イマココ!)
・ベクトルの活用(内積・外積・三角関数)
前回はベクトルを駆使してノードの回転成分を分解し、Bend=「曲げ」成分を抽出して「捻り防止」のノードの作成方法を紹介しました。今回はRoll=「捻り」成分をQuaternion計算を使って抽出していきたいと思います。
Result:結果を先に
前回と同じ手法を用いてノードのBend成分を抽出し、元の回転成分から打ち消すことによって、Roll成分のみを抽出します。
さて、Bend成分の抽出は前回取り上げましたが、ここからどうやってBend成分を回転成分から打ち消すのでしょうか。そもそもなぜ打ち消すとRoll成分を抽出できることになるのでしょうか。ひとつずつ考えていきましょう。
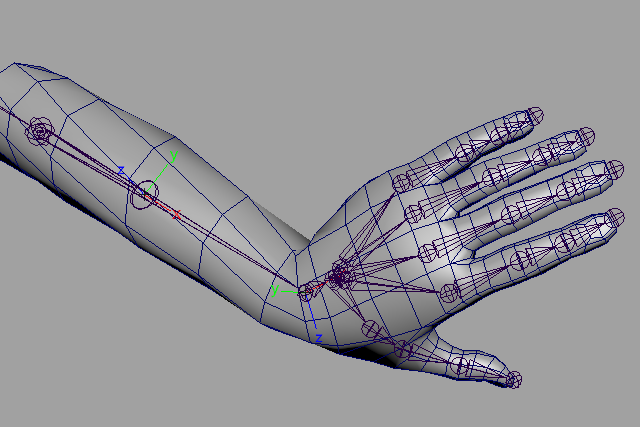
Step 01:「手首」の捻りを参考に、Roll制御について考えてみる
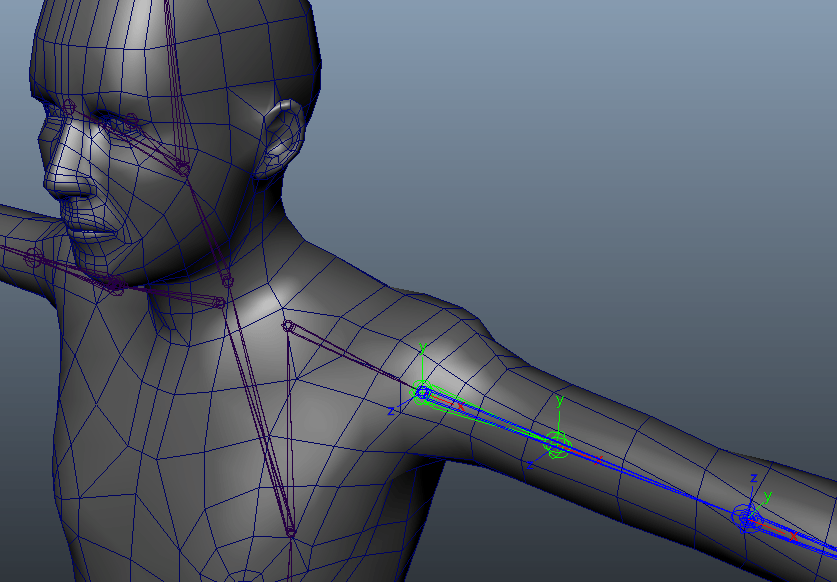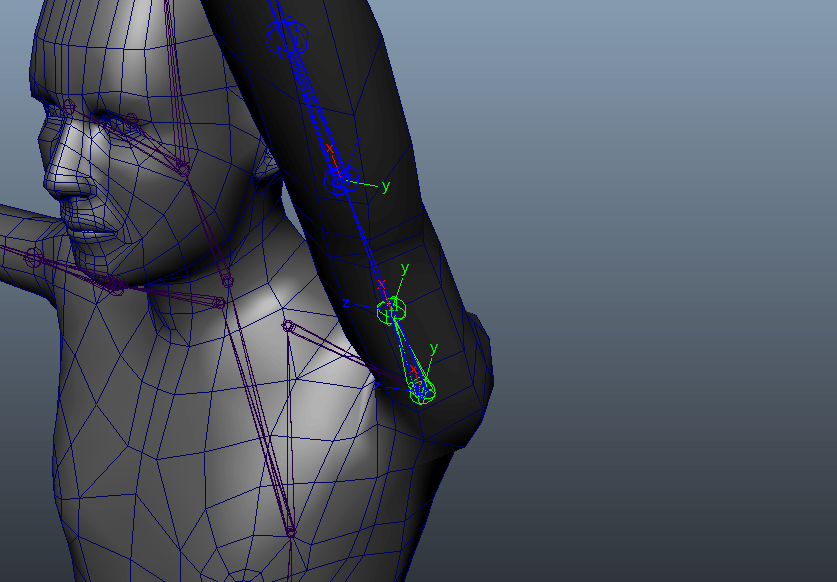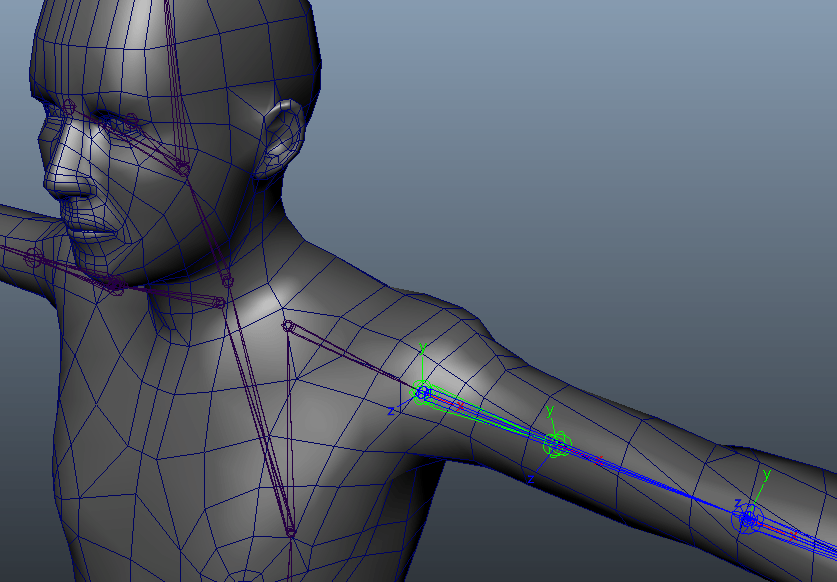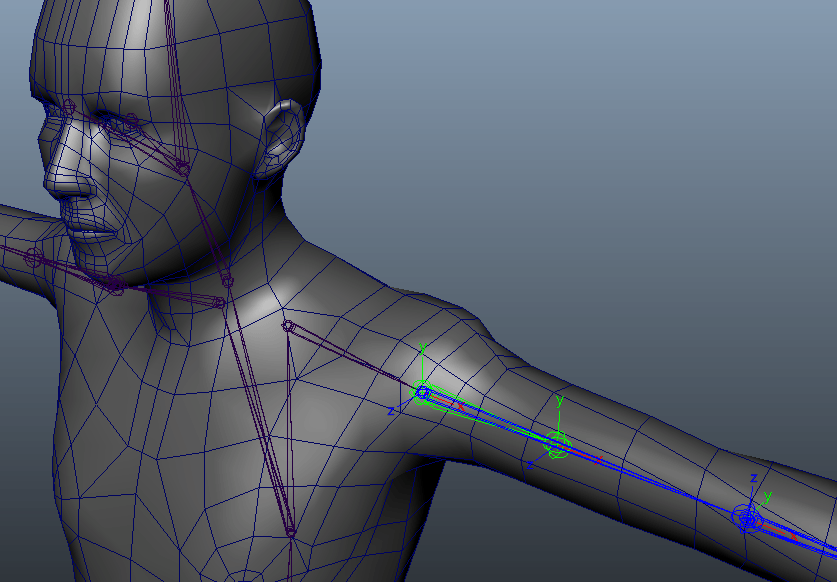
キャラクターの例では主に腕や足を捻った際、モデルの破綻を回避するために補助骨を徐々に捻らせる手法はポピュラーな例だと思います。二の腕や太もも・肘、膝などは、腕や脚における1軸の回転を考えれば良いので楽です。
オイラーでも簡単に実装できますね。しかし、手首の場合はどうでしょうか。先ほどの例と同じようにオイラー角の1軸で制御してみます。メインの軸をX軸として骨の軸方向を考えると、手首の捻りはX軸の回転を見れば良さそうです。
補助骨に手首のX軸回転の半分が入るようにノードをつなげて......
回してみると。
おっ。いい感じ?
しかし、手首を曲げて回してみるとどうでしょうか。
ちがう。そうじゃない。
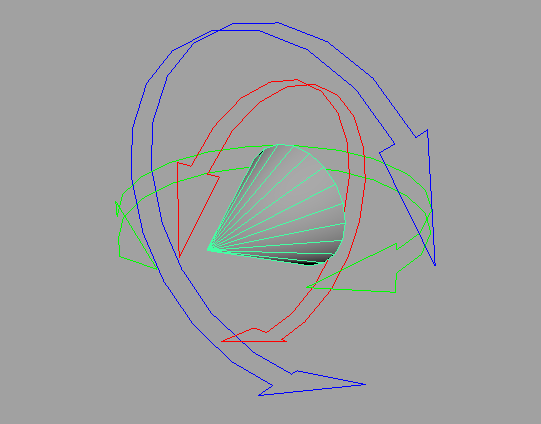
本当はこんな風に動くのが理想ではないでしょうか。
なぜ上手く制御ができなかったのでしょうか。
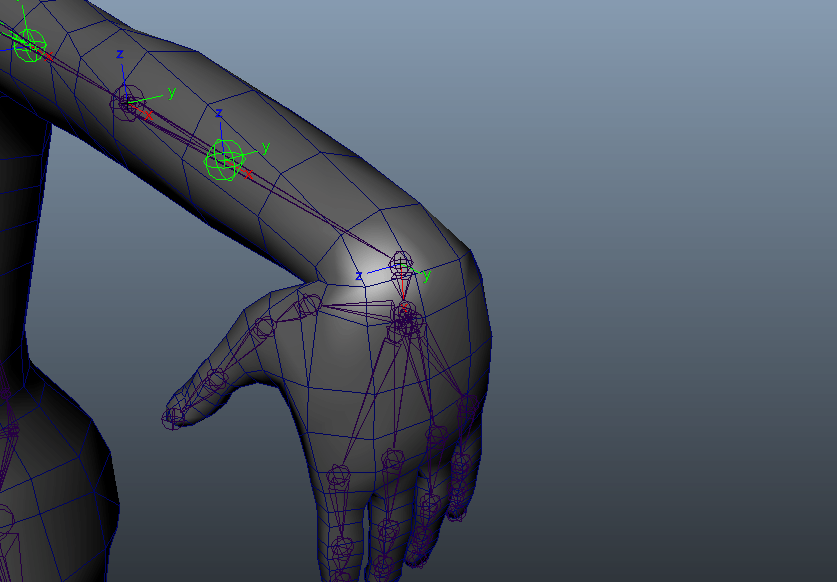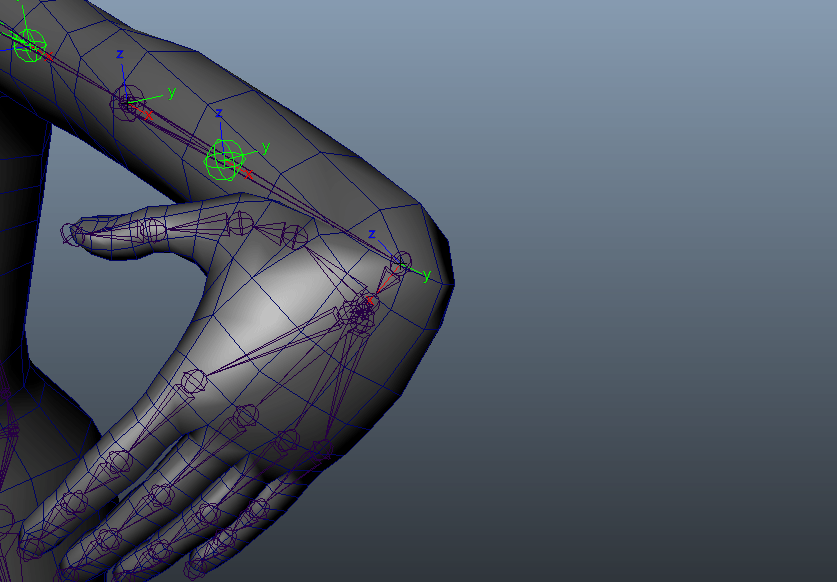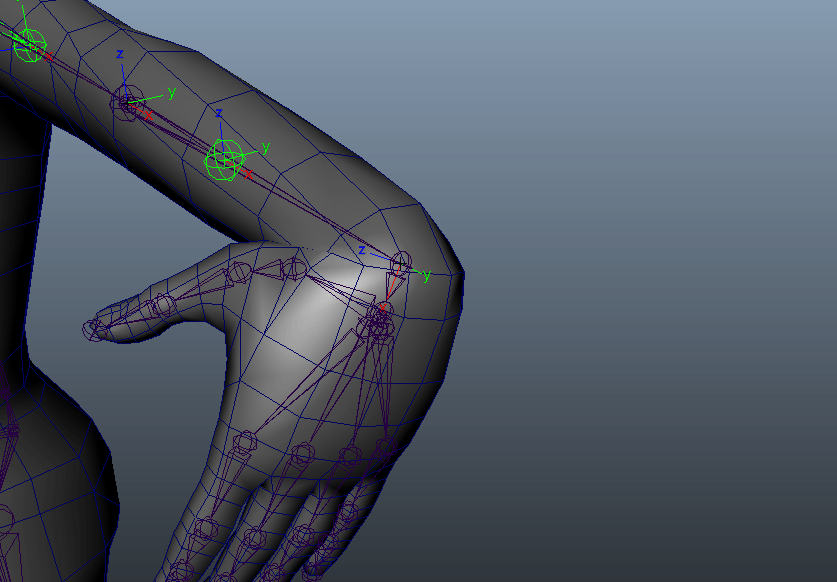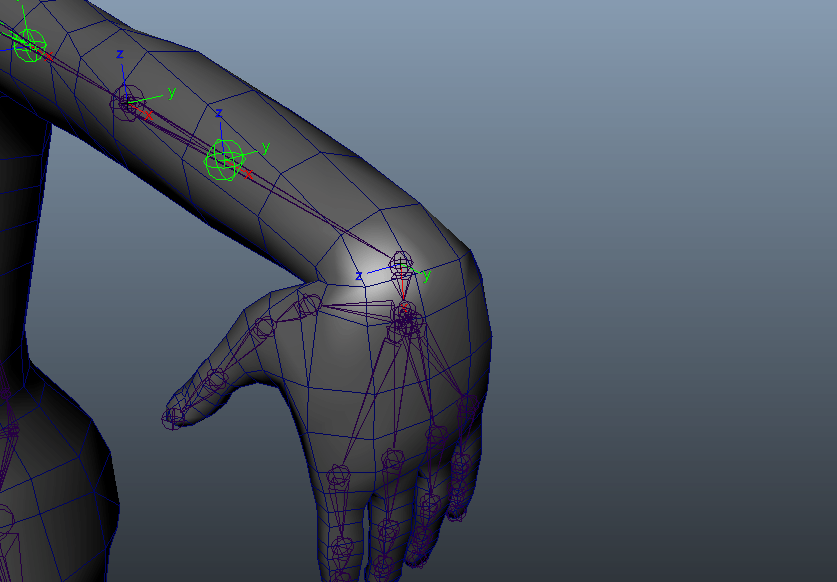
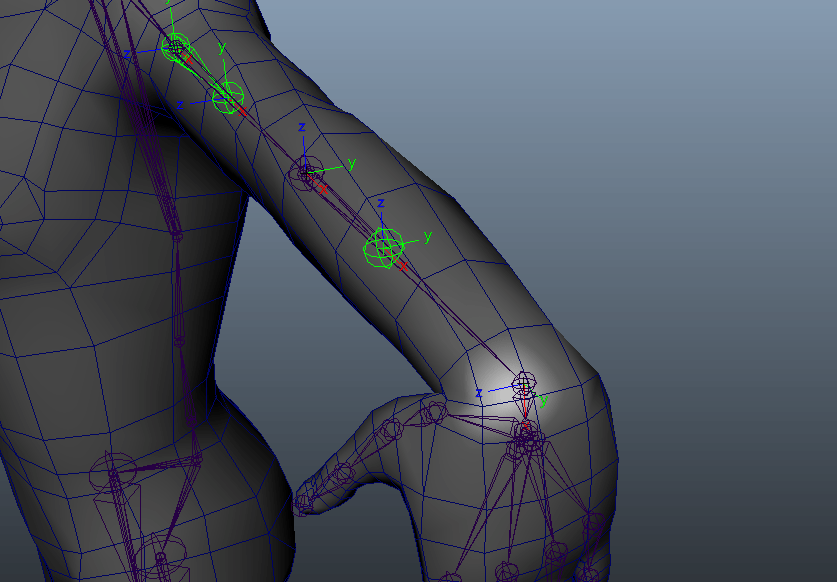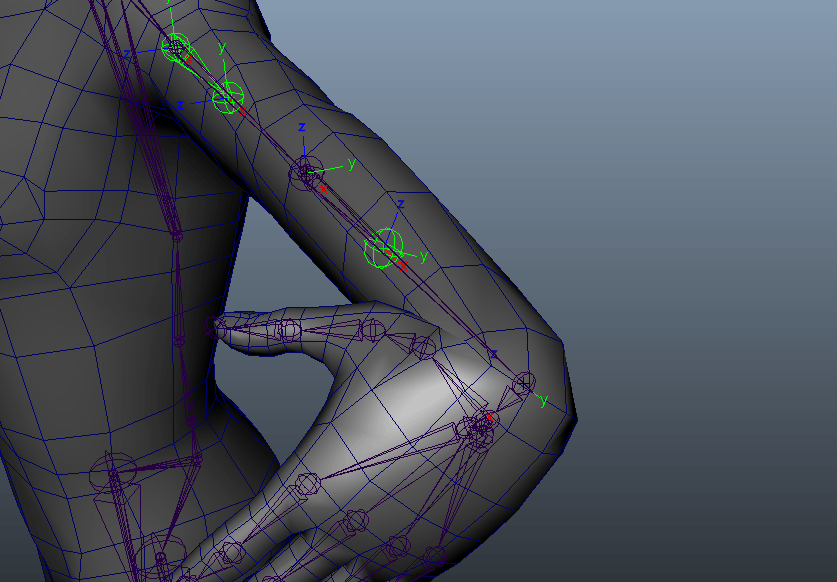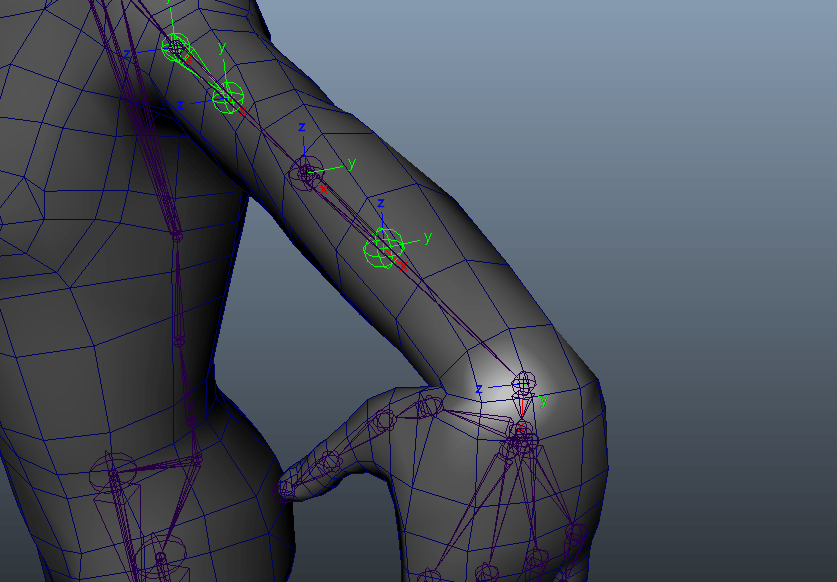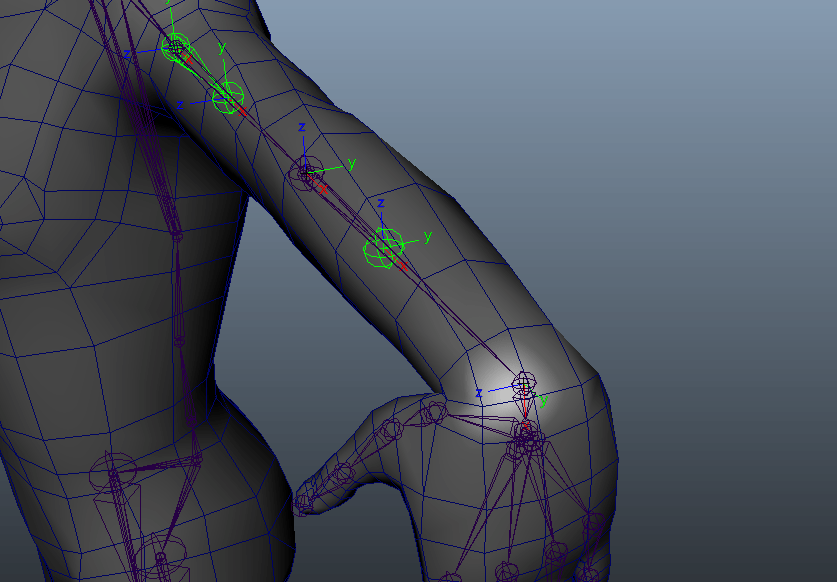
手首の場合は腕や脚の場合と違って、手首自身の回転状態によっては「捻り」として認識したい軸が変わりますね。
この場合はX軸ですが、
この場合はY軸になるように見えます。
このような制御を実現するには、一体どうすれば良いのでしょうか。
Step 02:回転成分からBend成分を打ち消す
「捻り」単体で考えると難しそうですが、前回の記事で「Bend = 曲げ」の制御は成功しています。
このように、左の手首のBend成分を抜き出して右側の手首に代入することで、現在の「曲げ成分」だけでノードを回転させることができています。ならば、回転成分からこのBend成分を打ち消すことによって、捻り=Roll成分を抽出することはできないでしょうか。
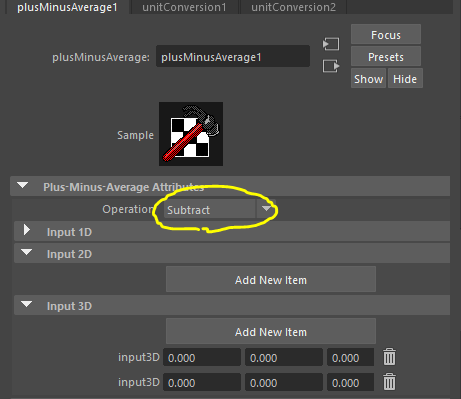
オイラー回転で試してみましょう。現在の手首回転とBend回転をplusMinusAverageノードにつなぎ、手首の回転からBendの回転を引き算させます。
結果は......
お! できたかも!?
思った通り、回転成分からBend成分を打ち消せばRoll成分を取り出すことができそうです。
次ページ:
Step 03:Quaternionについて考える
Step 03:Quaternionについて考える
ここまで、オイラー回転を使って補助骨の制御について考えてきました。しかし、オイラー回転をリグ制御に用いることの問題については前回の記事で触れた通り、直感的でわかりやすく操作しやすい反面、補助骨の制御には不向きです。
実際、このように挙動が暴れる場合もあって、運用には注意が必要です。
結局挙動が暴れる箇所を手作業で直す、などということになってしまうと、アニメーションの工数をいたずらに増やしてしまうことにもなりかねません。
そこで、Quaternionという回転制御の概念について少し踏み込んでみたいと思います。オイラー回転は「どの軸にどれくらい回ったか」という説明ですが、
Quaternionは、「どっちを向いていて、どれくらい捻じれているか」で、現在の姿勢を説明しています。
このように、オイラー回転に対してQuaternionは姿勢をダイレクトに説明しているので、補助骨制御の面ではQuaternionの方が向いている感じがしますね。
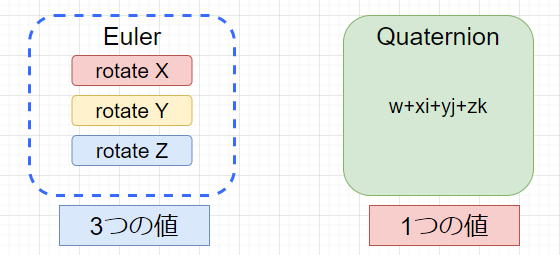
また、オイラー回転はX、Y、Z軸の3つが回転して現在の姿勢にいたるのに対し、Quaternionは「四元数」という「複素数」を拡張した1つの値による1回の回転で現在の姿勢にいたります。そのため、Quaternionにはオイラー回転にあるような「回転順序」の概念が必要ありません。
この点においても、補助骨制御やリギングにおいてはQuaternionを積極活用していきたいところです。
Step 04:Quaternionでの回転計算
では、Quaternionを使った回転制御について考えてみます。
オイラー回転では、回転加算は足し算だったのに対して......
Quaternionはかけ算で回転加算を考えます。
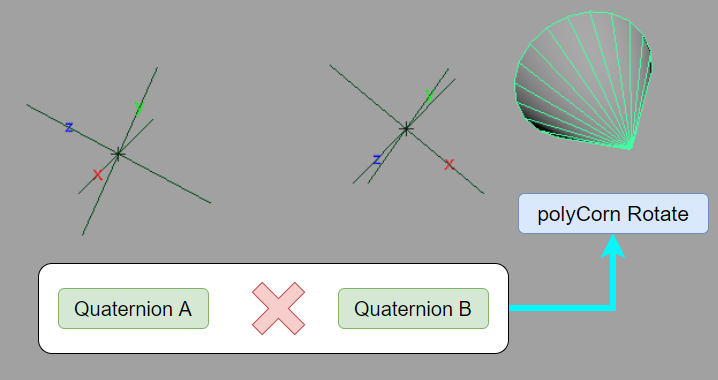
なので、例えばpolyConeノードに対して回転Aの後に回転Bをさせたい場合は、回転AのQuaternionに回転BのQuaternionをかけ、polyConeノードに接続すれば良いのです。
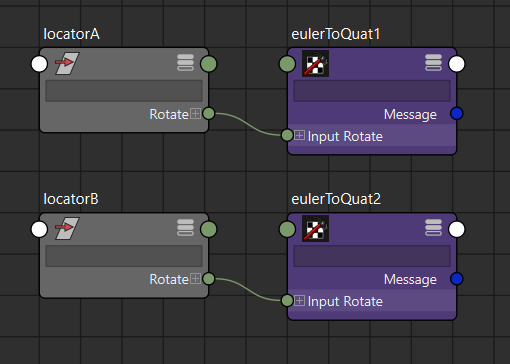
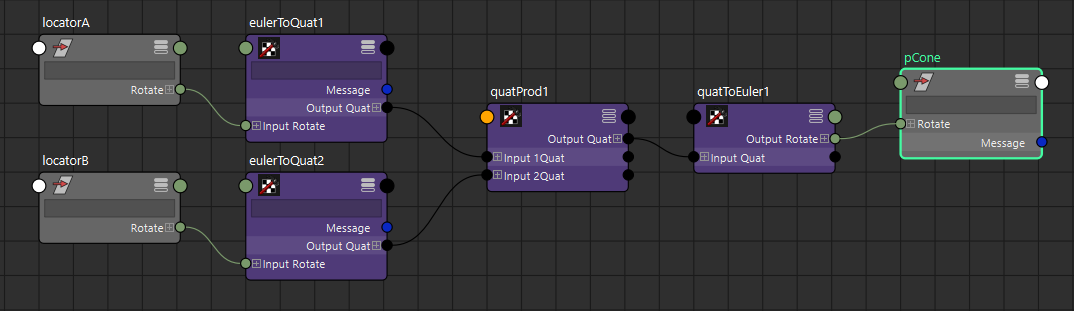
試しにノードエディタで接続を作ってみます。
locatorA、locatorBのオイラー回転をeulerToQuatノードを使ってQuaternionに変換し、
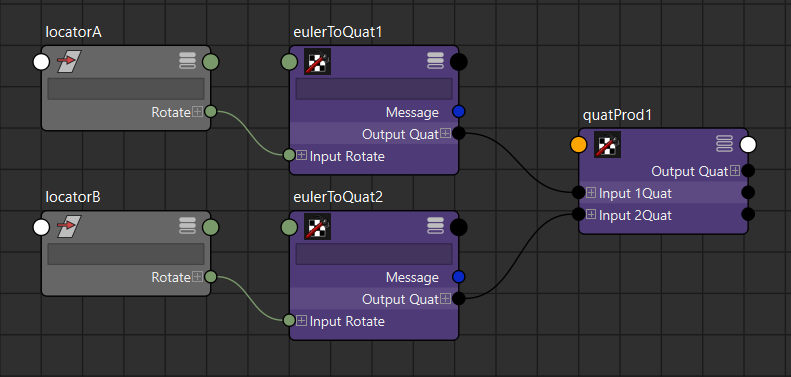
quatProdノードを使ってそれぞれのQuaternionをかけ算します。
quatToEulerノードを使ってQuaternionを再度Eulerに戻し、polyConeノードに接続すると、
このように、ノードAの回転の後にノードBの影響を受けていることがわかります。
では、回転加算がかけ算ならば、回転を打ち消したい場合は?
逆数をかければ良いのです。
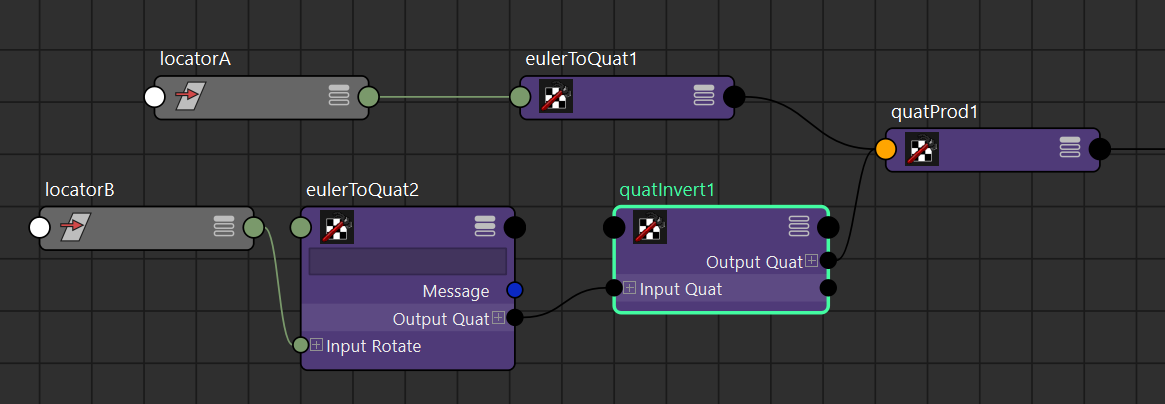
QuatInvertノードでQuaternionを逆数にすることができます。試しに先ほどのlocatorAのQuaternionをQuatInvertノードに接続し、逆数にしてみます。
すると......
このように、回転Aを回転Bから打ち消した結果がpolyConeノードに流し込まれていることがわかります。ちなみにQuatInvertノードによって取得されたQuaternionは、逆Quaternionとも呼ばれます。
Step 05:実装
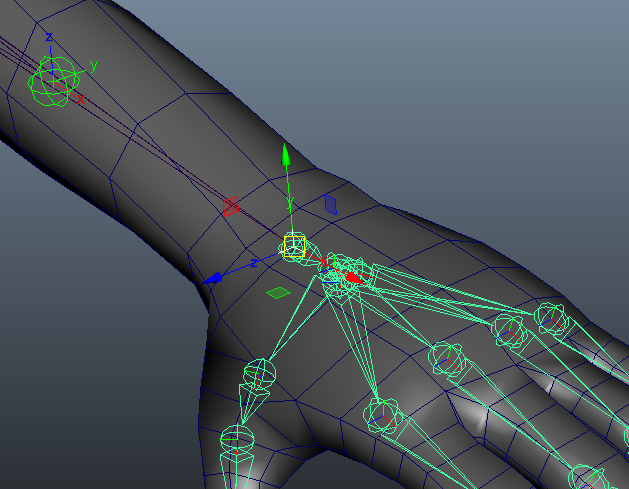
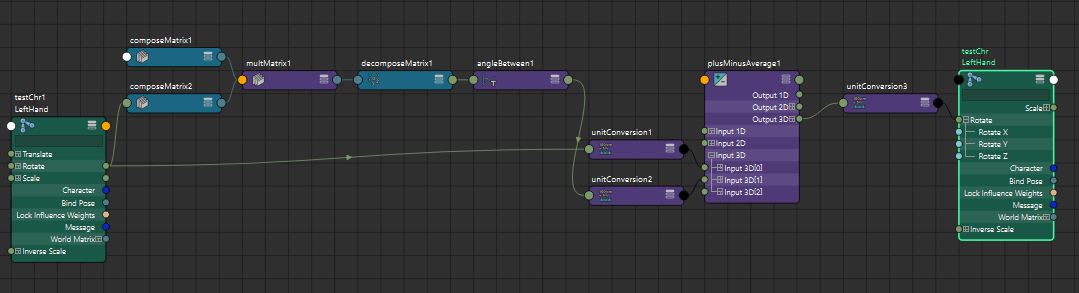
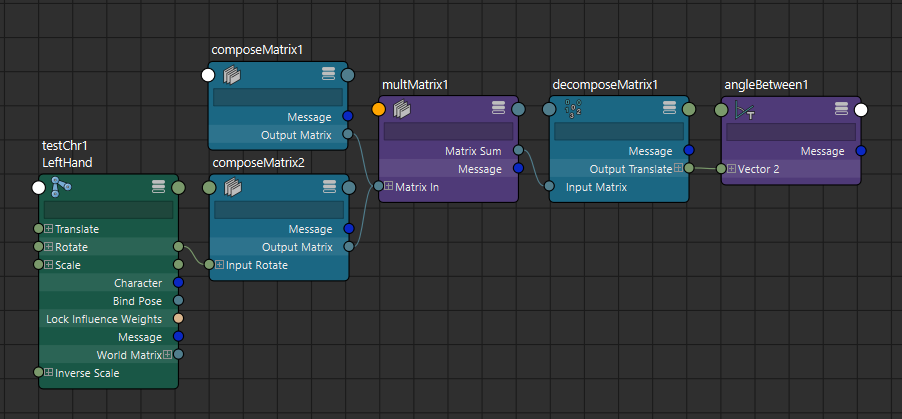
さて、ここまでで行なった設計を最初の手首ジョイントに適用してみましょう。まず、手首のBendを取得するノードを構築します。
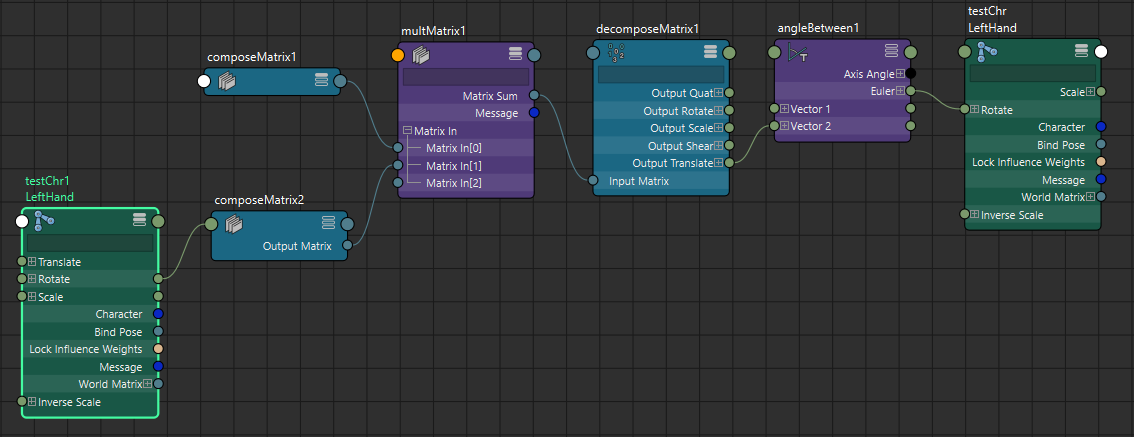
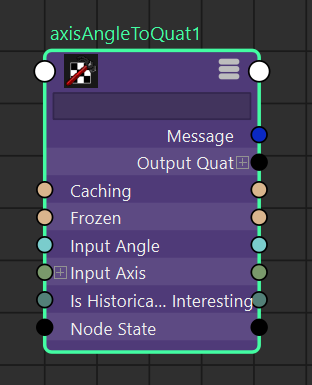
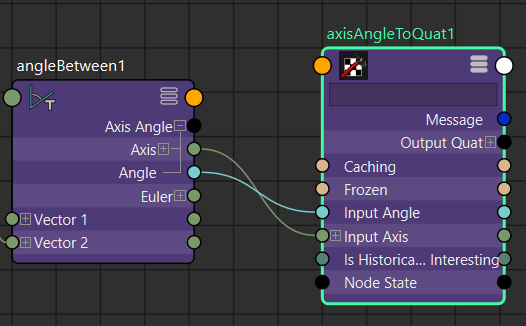
今回は純粋にジョイントの回転成分のみを扱いたいので、ジョイントのrotateのみをcomposeMatrixノードに接続してMatrixを生成しています。次にBend回転をQuaternionに変換しますが、axisAngleToQuatノードを使うと、回転軸と角度情報からQuaternionを計算することができます。
Bend回転を取得しているangleBetweenノードからAxisとAngle情報をaxisAngleToQuatに接続して、Quaternionに変換します。
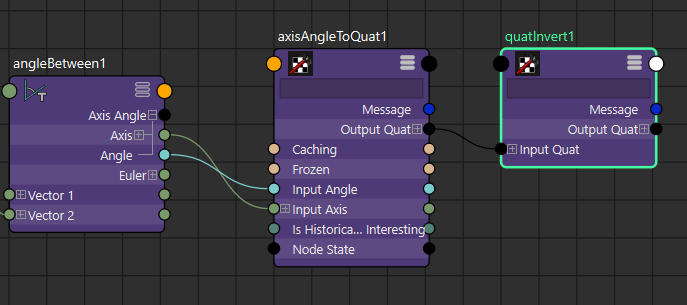
続いて、このQuaternionをQuatInvertノードに接続して逆Quaternionに変換しておきます。
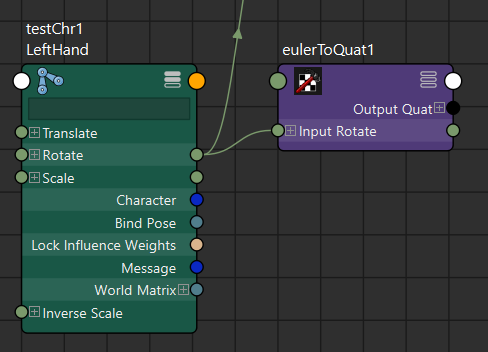
次に、手首自身のEuler回転をeulerToQuatノードに接続してQuaternionに変換します。
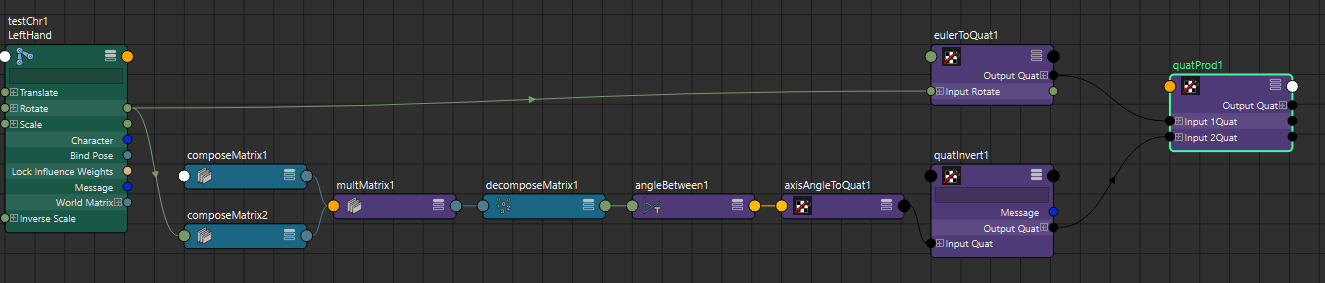
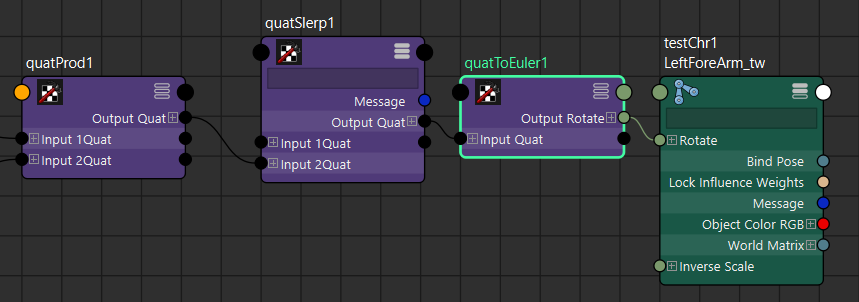
QuatProdノードを作成して、手首のQuaternionにBendの逆Quaternionをかけ算します。
これでRollのQuaternionが抽出できたはずです。
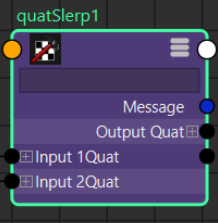
さて、ここで緩衝のためにRoll成分のうち半分くらいを取り出したいところです。オイラーに変換した後、値を半分にしても良いのですが、ここではquatSlerpノードを使ってみます。
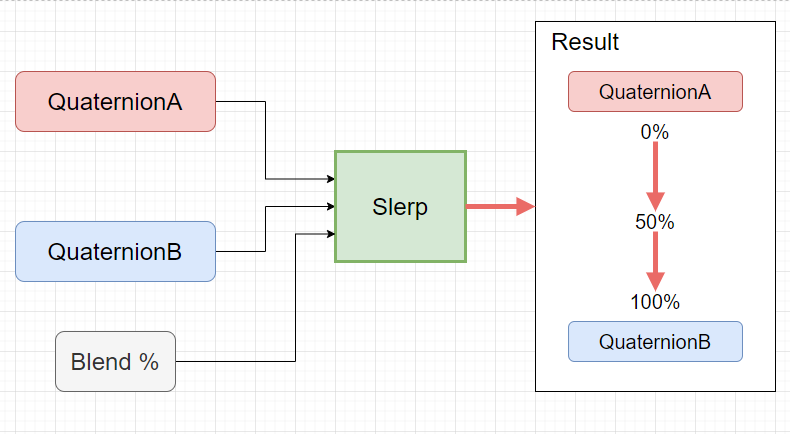
quatSlerpノードは2つのQuaternionの入力に対して、指定の係数でSlerp補間をかけることができるノードで、平たく言うと、0%のときはQuaternionAを返し、100%のときはQuaternion Bを返し、50%のときは半分を返すというもので、pairBlendノードやコンストレイントのウェイト値のように使うことができます。
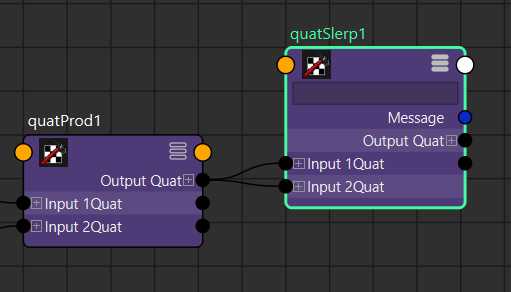
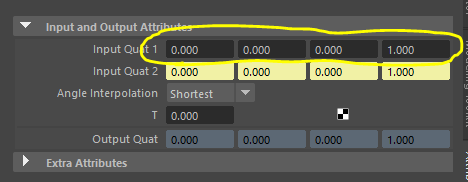
ひとまずquatSlerpノードを生成し、input1とinput2両方にRollのQuaternionを接続します。
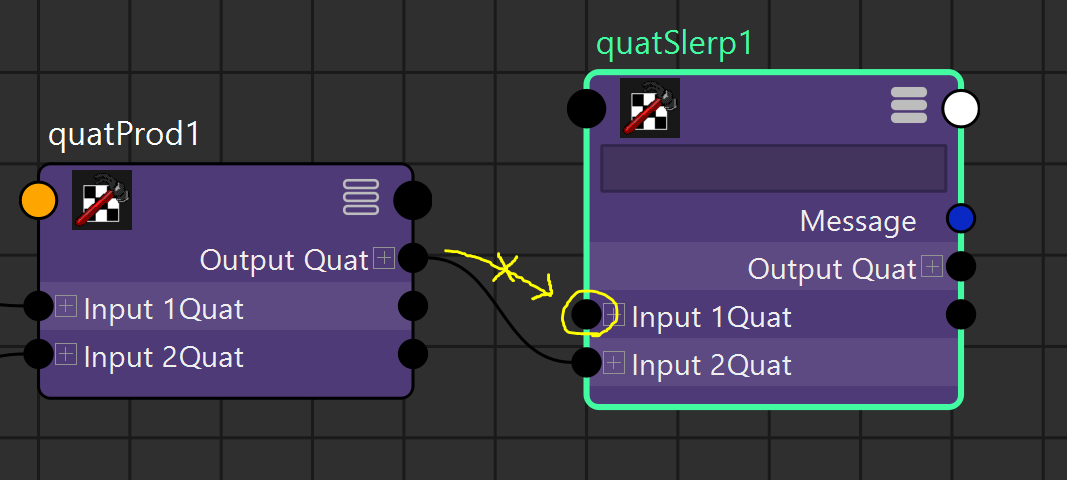
次に、input1からQuaternionの接続をカットします。
これで最初の値、すなわち規定値=無回転の状態の値をinput1に残すことができます。
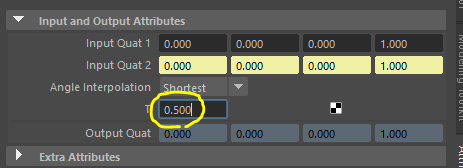
そして、大体半分くらいのRollになるように、Tの値に「0.5」を入力しておきます。
結果のQuaternionをquatToEulerノードに接続してオイラー回転に変換し出力の値を補助骨のrotationに接続します。
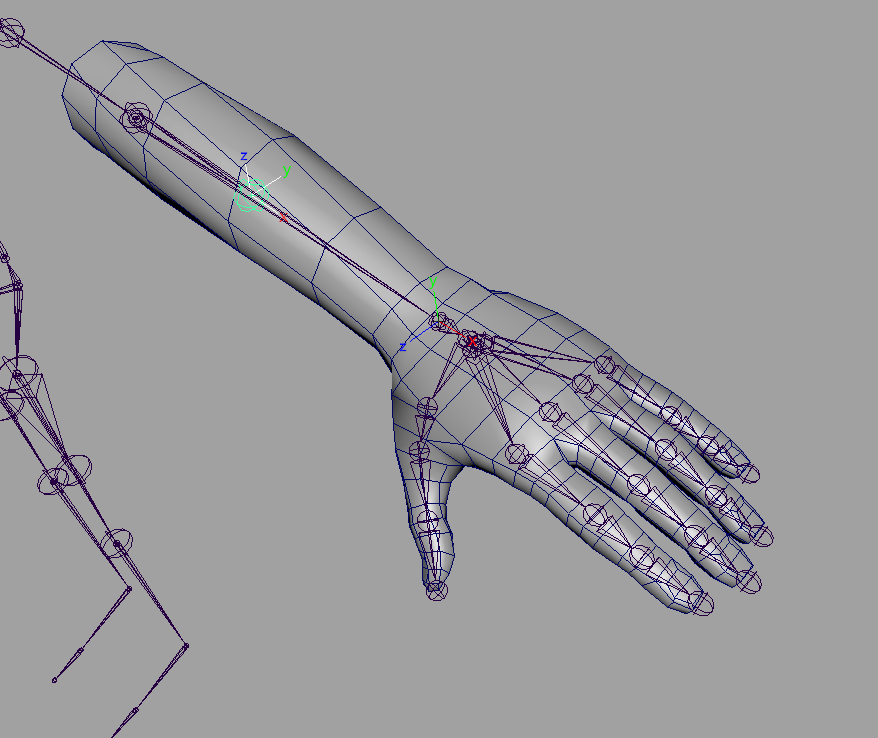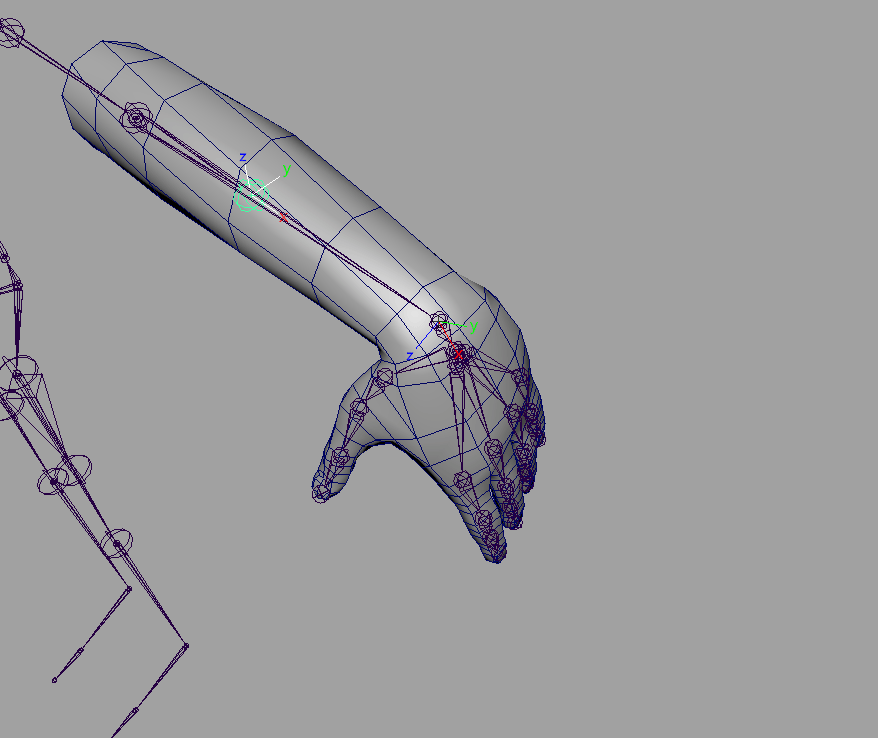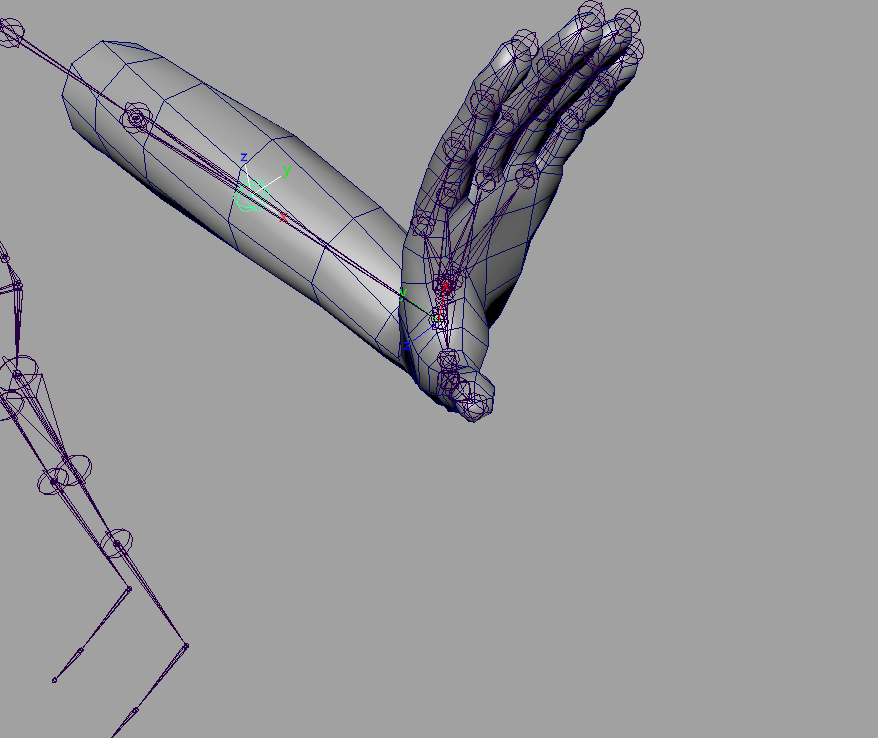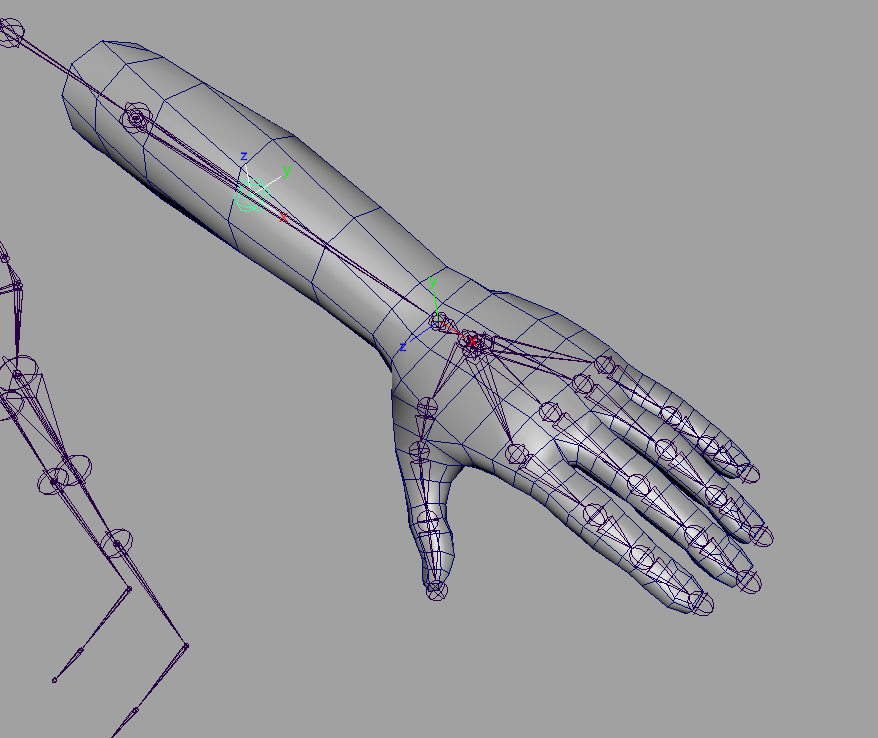
結果を見ると...
できました! ハラショー!
次ページ:
おまけ:なぜQuaternionはかけ算で回転加算になるのか?
おまけ:なぜQuaternionはかけ算で回転加算になるのか?
Quaternionの回転計算について少し踏み込んだおまけです。
そもそも、どうしてQuaternionはかけ算で回転加算になるのでしょう。
なぜ足し算ではだめなのでしょうか?
これは、
「厳密にいうと、Quaternionをかけ算すると回転になる」
というよりも、
「Quaternionのかけ算で回転を表現できるので便利」
という認識のほうが正しいかもしれません。
でも別に、ここを深く理解せず「そういうものだから!」で飲み込んで先に進んでもまったく問題ないと思います。いわゆる「公式」のように認識して、どんどん先に進むべきです。
しかし、ここを理解した上で飲み込みたい人もいるはず。 ですので、ほんの少し深掘りしてみましょう。
Point 01:Quaternion=四元数は複素数の拡張
先に述べたように、Quaternionは複素数を拡張した概念です。ここでは複素数のかけ算を例として紹介し、Quaternionがなぜかけ算で回転加算になるのかの理解へつなげたいと思います。
Point 02:複素数は想像上の数(かず)!
まず初めに、二乗して1になる数値って何でしょうか。
答えは、1と-1ですね。
では、二乗して-1になる数値は?
答えは、自然界には存在しないということになっています。
でも、昔の数学者の人たちは考えました。
「もし二乗したら-1になる数値が存在したら...?」
数学者は、この想像上の値=「Imaginary number」を、頭文字「i」を取って数式上表すことにしました。これが虚数です。
では、自然界に存在する数(かず)=実数と虚数を足し算したらどうなるでしょう?
その数値は交わることができないので、このように「実部」と「虚部」をもつかたちで表すことができます。この実数と虚数を足した値を「Complex number」、すなわち「複素数」と呼びます。
Point 03:複素数を平面上に表してみよう
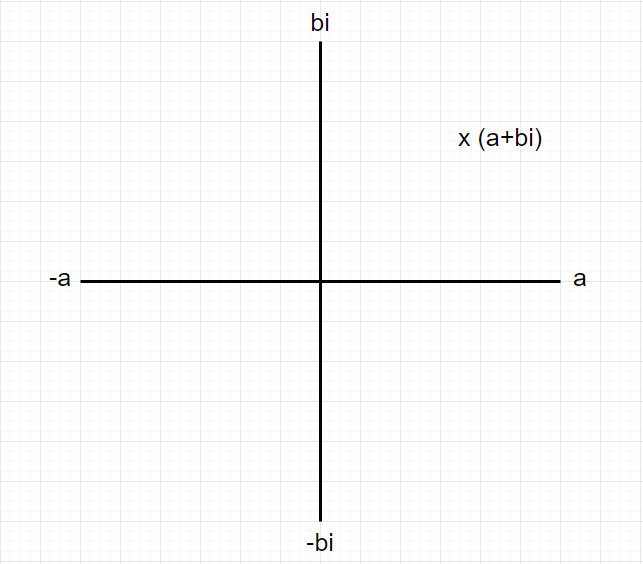
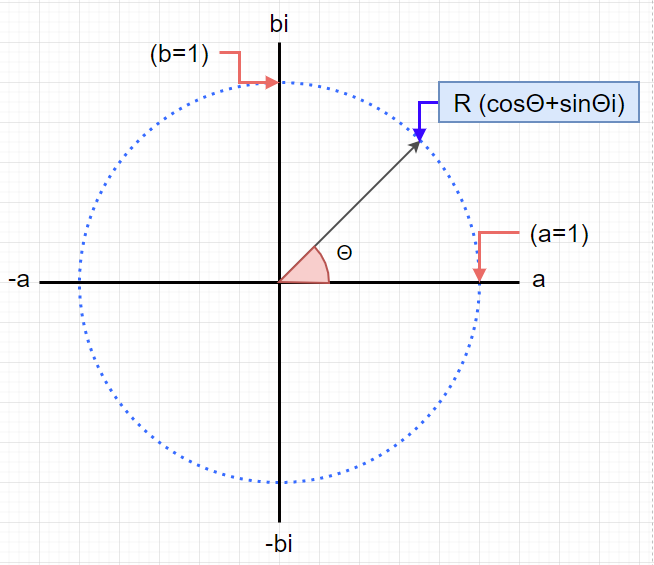
縦軸を虚部、横軸を実部とした平面を作って、2次元的な側面で複素数を考えてみたらどうなるでしょう?
複素数(a+bi)は上記のように表すことができます。
このような複素数を表す平面を「複素数平面」と呼びます。
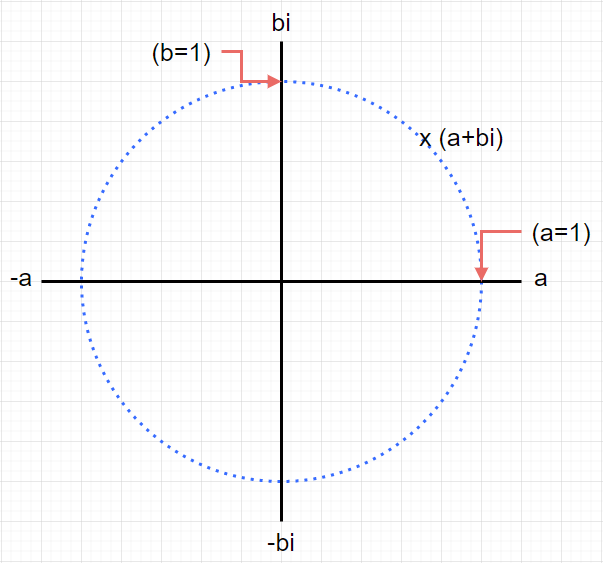
ここに、原点から半径1の単位円を重ねてみると、こんな風になりました。
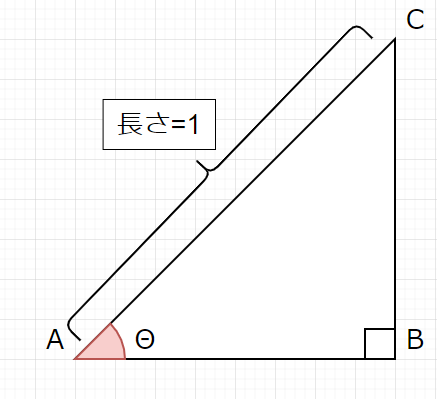
円Oは半径1の単位円なので、円周上の点Rはこんな風に表すことができます。
上記は長辺1の直角三角形に対する三角関数で計算することができます。
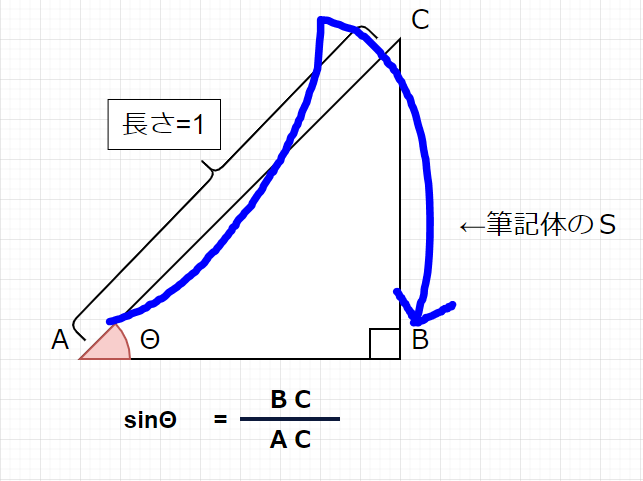
上記の三角形での辺BCの長さはsinΘで表すことができるし、
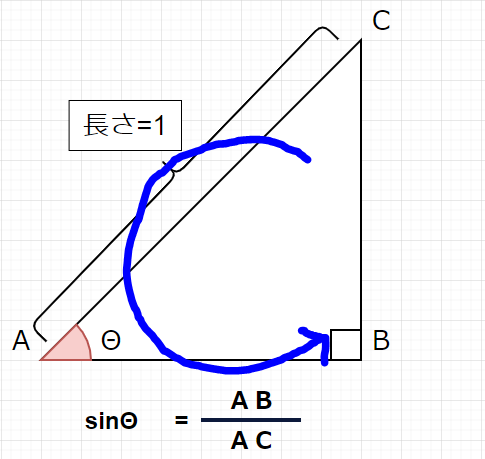
辺ABの長さは同様にcosΘで表すことができます。
上記のような「覚え方」の図は、高校数学の授業で出てきたのではないでしょうか。筆者はいまだにこの図を使っています。
Point 04:複素数のかけ算を複素数平面で2次元的に考えてみると......?
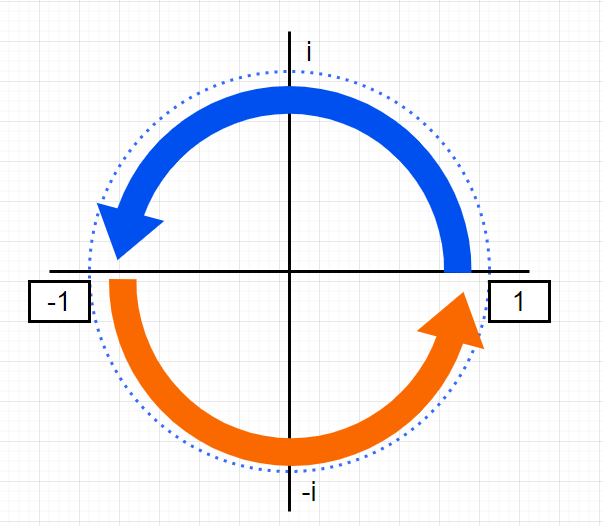
先ほど出てきたように、-1は二乗すると、1になります。
複素数平面で考えると、こうです。
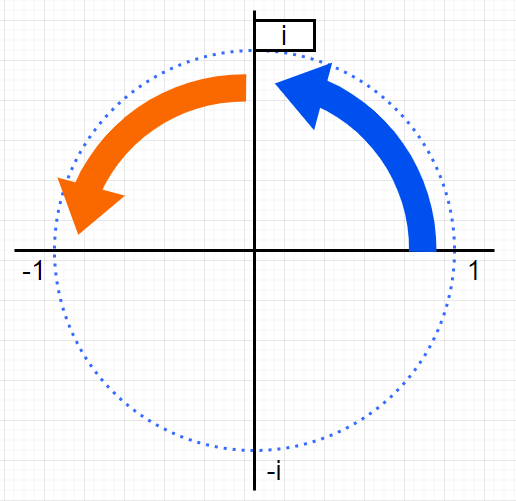
では、iを二乗すると?
-1なので複素数平面上ではこうです。
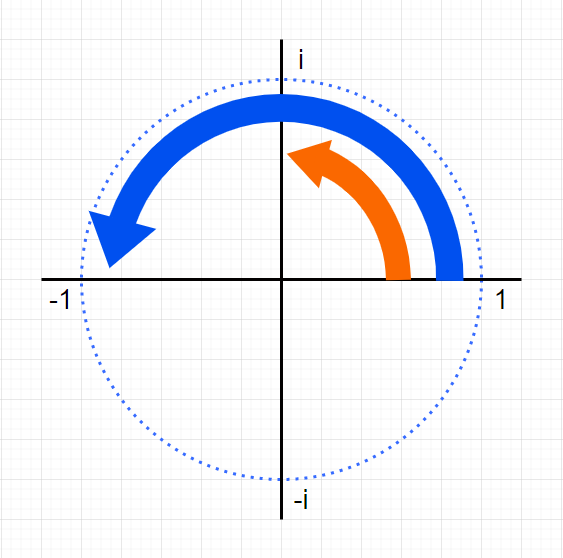
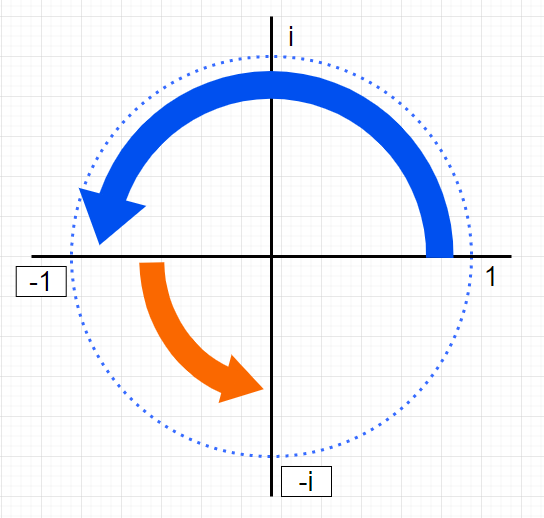
では-1にiをかけると?
-iになります。
ここで気づくべきは、複素数平面上で見ると、複素数のかけ算は回転加算になっているように見える......ということなのです。
果たして本当にそうでしょうか?
Point 05:複素数のかけ算の式を展開して考えてみる
上記のように、複素数のかけ算が回転加算になっているのだとすると、
(cosα + sinαi)×(cosβ + sinβi)
は
cos(α+β) + sin(α+β)i
になるはずですよね。
では、
(cosα+sinαi)×(cosβ+sinβi)
を展開してみましょう。
ここでは、三角関数の積和の公式を使って式を展開します。
●積和の公式
●式の展開
ほらね!!
このように、複素数平面において、単位円上にある複素数同士のかけ算
(cosα+sinαi)×(cosβ+sinβi)
は、(cosα+sinαi) の角度αをβ分追加回転させたことに等しい、と言えるわけです。
つまり言い換えると、
複素数のかけ算で回転が表現できる
ということになるのです。
以上はあくまで2次元上の計算でしたが、これを立体で考えられるよう拡張されたのが四元数、すなわちQuaternionになります。
数学って意外とグラフィカルな側面がありますね!
いかがでしょうか!
以上で示した通り、複雑な回転制御でも回転成分を分解して考えることでシンプルな実装が可能になります。
また、補助骨制御におけるオイラー回転の導入がリスキーであることも一部紹介いたしました。もちろんオイラー回転が全てNGなわけではないと思いますので、導入の際は用途をよく考えて設計すると良いでしょう。
さらにおまけでは、なぜQuaternionはかけ算で回転加算になるのか少しだけ追究してみましたが、数学のグラフィカルな面に触れられたのではないでしょうか。
次回は「ベクトルの活用(内積・外積・三角関数)」と称して、この数学のグラフィカルな面にアプローチしていきたいと思います。
いやー、リギングってホントに面白いものですね!
では今回はこの辺で!
サヨナラ!サヨナラ!サヨナラ!!
Profile.
-

-
山本智人/Tomohito Yamamoto(COYOTE 3DCG STUDIO)
ゲーム開発会社にてグラフィックアーティストとして、モデリング・モーション・エフェクト・UIなどオールラウンドのグラフィック制作を経験後、テクニカルアーティストに転身。現在は株式会社クリーク・アンド・リバー社 COYOTE 3DCG STUDIOにて、社内外問わずアーティストのDCCツールサポートや制作パイプラインの提案・作成・運用を行う。特にアニメーション制御やモーション制作周りのテクニカルサポート・リガーとして様々なプロジェクトに従事