2015年8月26日(木)、「CEDEC 2015」にて「サブディビジョンサーフェスのすべてがわかる・グラフィックスエンジニア向け理論編」と題し、ピクサー・アニメーションスタジオの手島孝人氏ならびに、DeNAの松岡 徹氏による講演が行われた。 Catmull-Clark サブディビジョンサーフェスの数学的な基礎やハードウェアテッセレーションに関して手島氏が、レイトレースに関して松岡氏が講演した。両氏の講演を通して近年のサブディビジョンサーフェスの技術動向を概観する。
<1>OpenSubdivにおける取り組み
まず、手島氏の講演からふりかえる。2012年のSIGGRAPHにてPixarより発表されたオープンソースプロジェクト「OpenSubdiv」は、インハウスで開発してきたサブディビジョンサーフェス技術をオープンソース化したプロジェクトだ。サブディビジョンサーフェス技術は、法線がきちんと計算できるという利点がある(手動で個別に調整する必要がない)。

講演を行う手島孝人氏(Pixar Animation Studios)Graphics R&D, Senior Software Engineer
頂点に法線を与えるのは、滑らかな面を表現するためである。曲面を表現する場合、ポリゴン起点のワークフローと曲面起点のワークフローが考えられる。
一般的なポリゴン起点のワークフローでは、ローポリで作成された形状にサブディビジョンをかけていき、ハイポリとなって理想形状に近づく。しかし、ハイポリ化にはきりがなく、ポリゴン数の多い形状を扱うと、データ量も増大する。
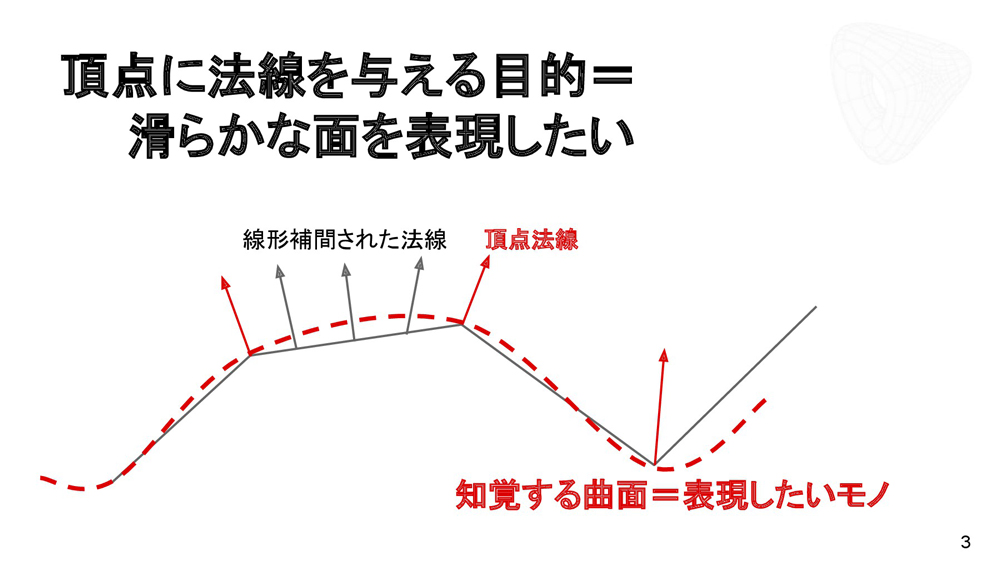
一方、曲面起点のワークフローでは、理想形状からサブディビジョンを経て曲面表現を行い、近似をとってポリゴンの形に落とし込んでいく。この方式では任意の精度で出力でき、またコンパクトな高次表現が可能となる。
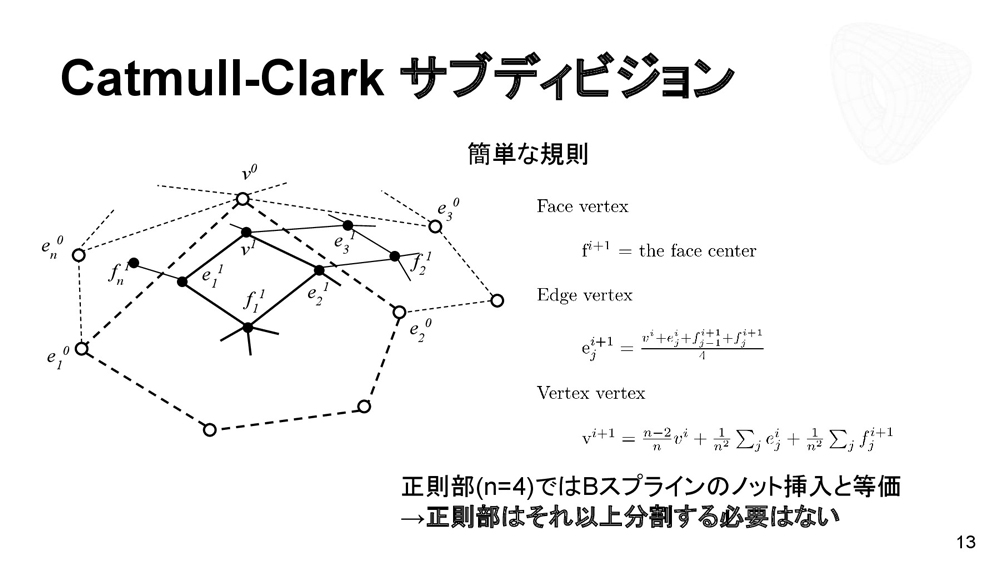
この技術に使われているCatmull-Clarkサブディビジョン・サーフェースとは、双3次一様Bスプラインサーフェスの拡張表現である。そして、あらゆるメッシュトポロジに対応(基本的には2次元多様体)が可能である。特徴としては、割れ目、折れ目がなく(ハードエッジのようにはならない)、仕上げが美しい点が挙げられる。
双3次一様Bスプラインには、自動的にC^2連続、制御点の数がベジェより少ない、凸包性・変動減少性があり、結果が予測しやすく交差判定が単純である、ローカルサポート(局所的に編集ができる)がある、直線が厳密に表現できる(曲線区間との接続もC^2連続)、計算がシンプルで座標のみを必要としノット・ウェイトなど追加データが不要である、3次ベジェとの変換も容易である、といった利点がある。
一方で、以下のような問題もある。トポロジに大きな制約がある(グリッド、円柱、トーラス型しか作れない、つまりほとんどのキャラモデルを作ることができない)、二次曲面(円柱や球)が厳密に作れない(ただしこれはゲーム、映画ではあまり問題にならない)、といった点だ。
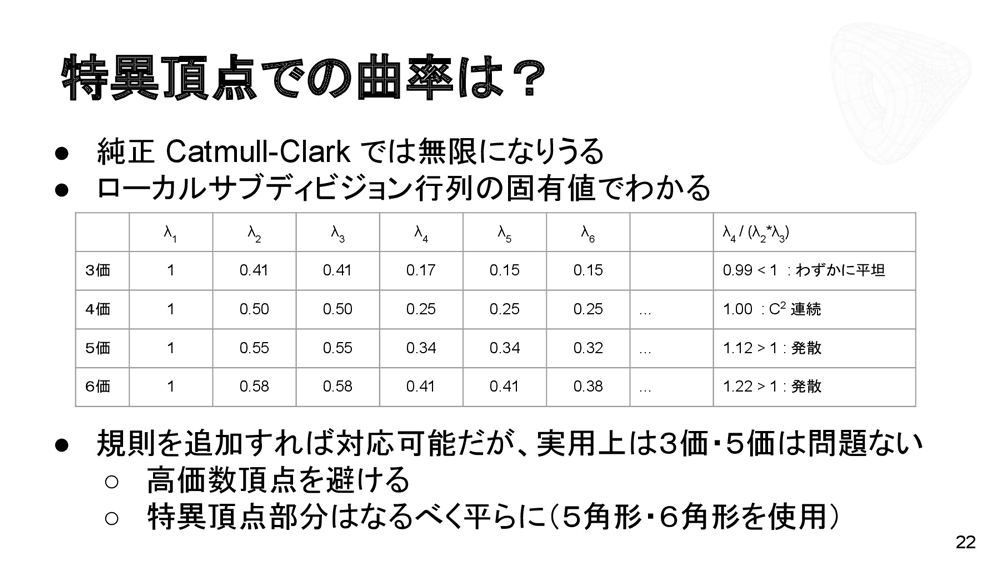
真円を例にとると、制御点の形状が四角形の場合は真円との誤差が2.8%、六角形の場合は0.4%、と、制御点の数、形状によって誤差が変化していく。気をつけなければならないのは、分割が多ければ描画が美しくなるというわけではないということだ。サブディビジョンでは周辺の特異頂点の価数が上がってしまうため、シワになりやすい。
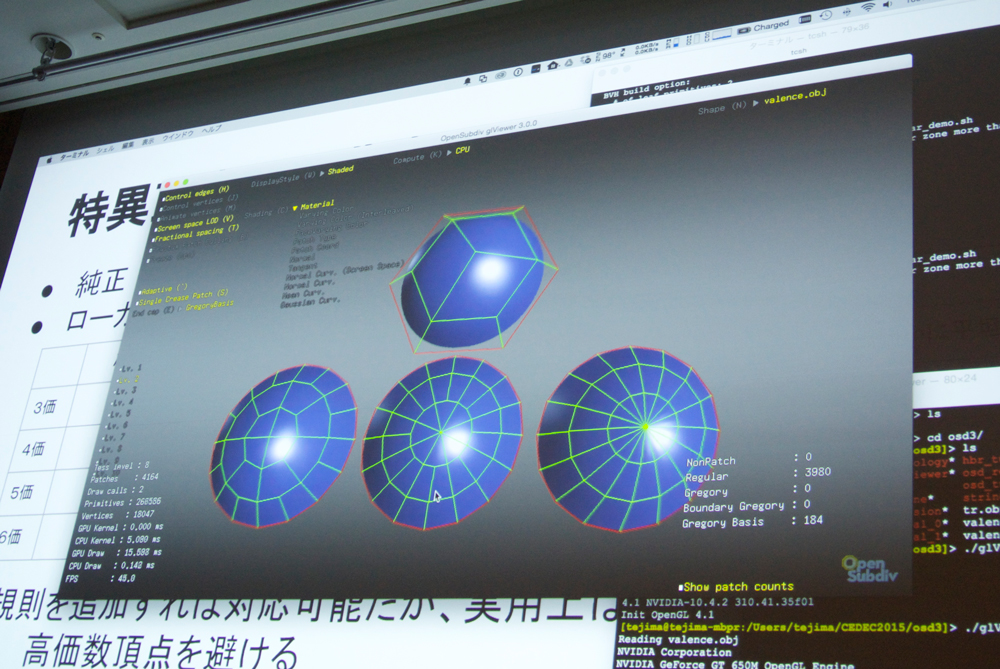
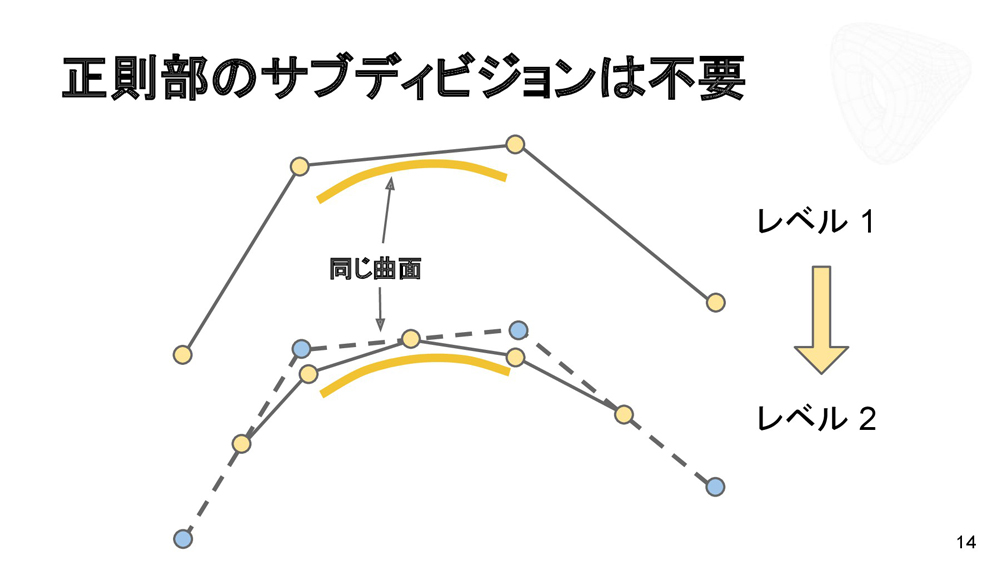
グリッドメッシュ以外も曲面で扱いたいというケースでも、サブディビジョンサーフェスが活用される。エッジが4つの正則頂点と、それ以外の特異頂点で対処がかわる。正則部はそれ以上分割する必要はないが、特異点部に関しては再帰的に求める方法を考える必要がある。リミット解析はそれぞれに行われる。
ハードウェアアクセラレーションに関して、もっと簡単にリミットサーフェスを描画したり、ハードウェアテッセレーターを使用できないか、という要請から、グレゴリーパッチと特徴適応分割の二つの手法が考案され使用されている。
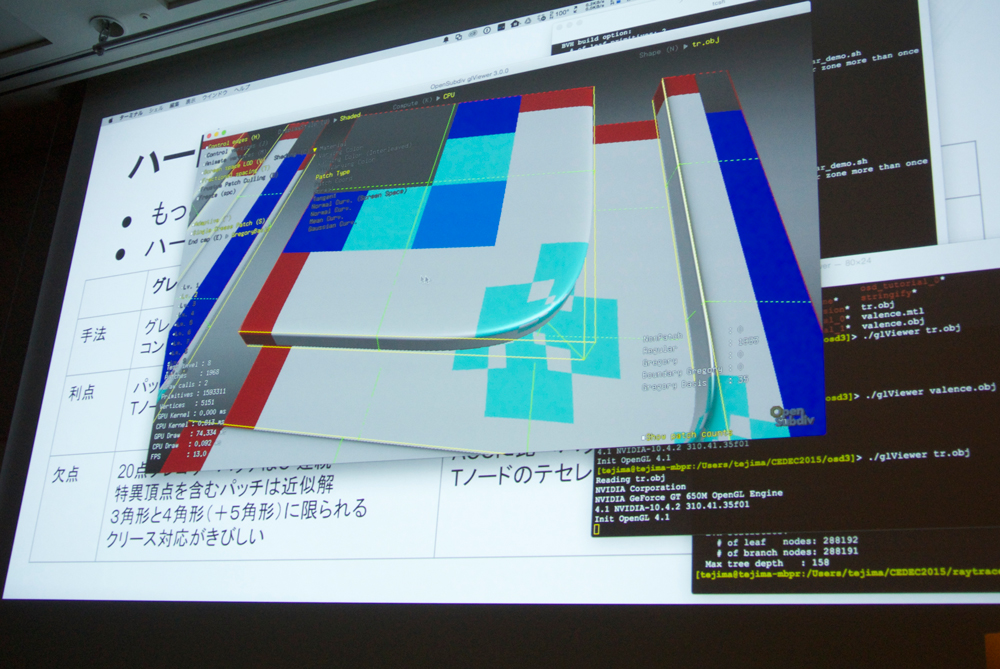
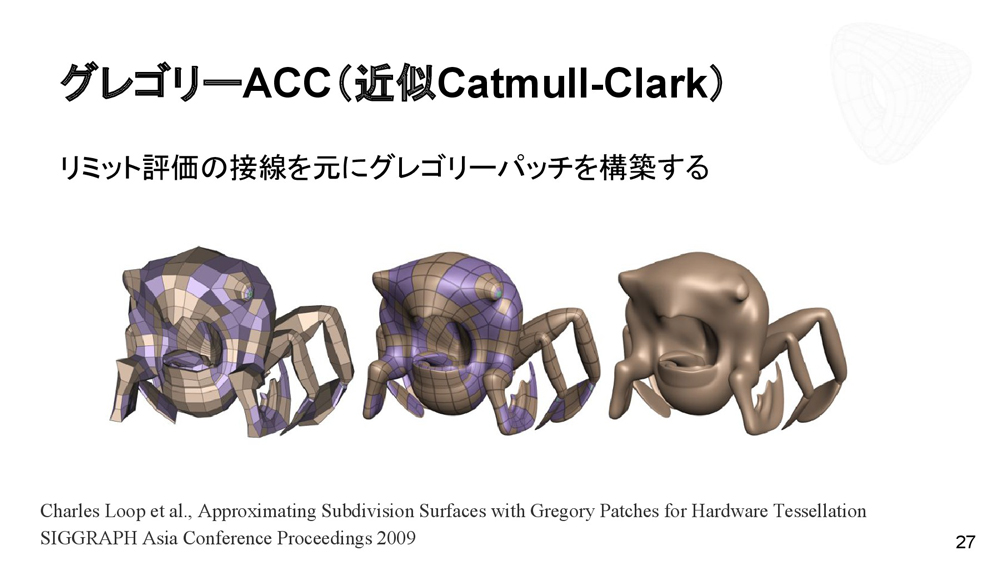
グレゴリーパッチは1983年に開発、CADで実用化されている手法である。Bスプラインと比較するとパッチ毎の制御点は増えるが、使い方によっては非常に便利である。ACC(近似Catmull-Clark)のメイン手法であり、隣接パッチとのC^1連続を自由に構成可能である。グレゴリーACCでは、リミット評価の接線を元にグレゴリーパッチを構築する。
<参考>
"Approximating Catmull-Clark Subdivision Surfaces with Bicubic Patches" by CHARLES LOOP(Microsoft Research)and SCOTT SCHAEFER(Texas A&M University)
[[SplitPage]]
<2>特微適応分割手法の登場
Bスプラインのみの描画を目的として、特徴適応分割という手法が開発された(特異点周辺のみ必要な部分だけ分割する、Tノードは別途対応する)。メリットとしては、C^2が確保できる、制御点の数も比較的抑えられる、クリース、階層エディットに対応できる、というものがあげられる。1つのシェーダで処理が可能になる。
<参考>
"Feature-Adaptive GPU Rendering of Catmull-Clark Subdivision Surfaces" by MATTHIAS NIEßNER(University of Erlangen-Nuremberg)、CHARLES LOOP(Microsoft Research)、MARK MEYER and TONY DE ROSE(Pixar Animation Studios)

特徴適応分割でのTノードの対処に関しては、OpenSubdiv3.0で、tess coordのリマッピングで接合を実現し、1DrawCall描画が可能になった。
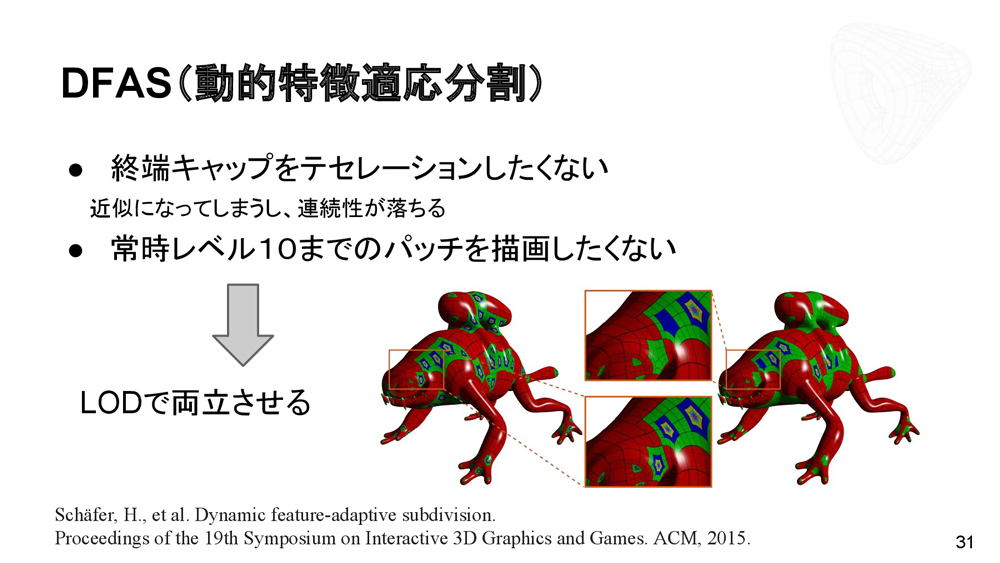
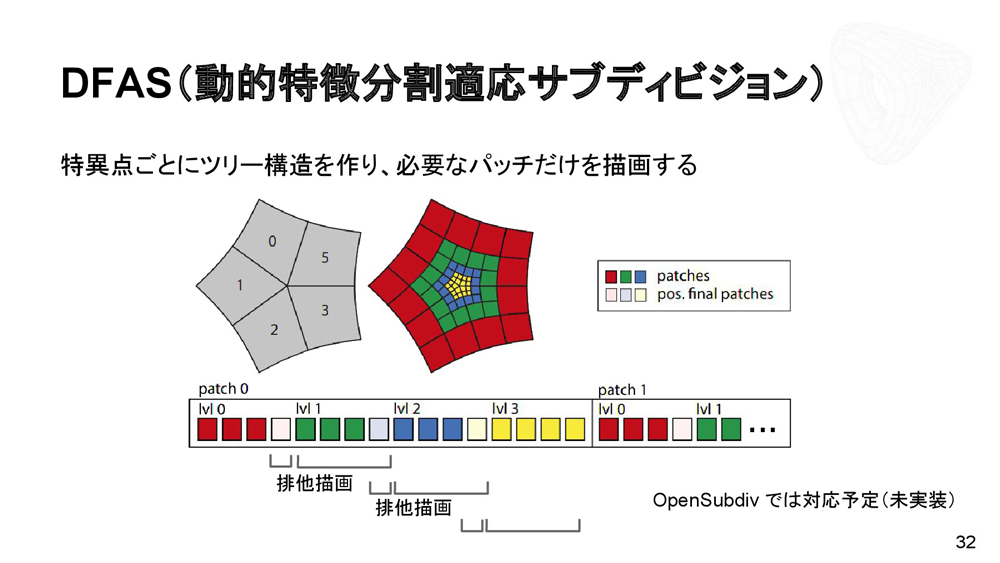
終端キャップに関しては、リミット評価で求めた座標と法線を使用してフタをするDFAS(動的特徴適応分割)という手法も開発されている。終端キャップをテセレーションしない、常時レベル10までのパッチを描画しないという設定を、LODで両立させることで可能にしている。
OpenSubdivでは対応予定である。特異点毎にツリーを作り、必要なパッチだけを描画するというものだ。
<参考>
"Dynamic Feature-Adaptive Subdivision"
セミシャープクリースという考え方も重要である。こちらは、短編『ゲーリー爺さんのチェス』(原題:Geri's Game)制作の際、純正Catmull-Clarkに追加された。
サブディビジョン過程でシャープ規則をs回適用、その後スムーズ規則を適用するというものだ。パッチごとにシャープネスの値を追加することが出来、モデルによってはパッチ数を大きく減らすことが出来る。OpenSubdivでは対応済みである。Vertexシャープネス、階層エディットは対応できないので、必要なまで適応分割を行う。
<参考>
"Efficient Evaluation of Semi-Smooth Creases in Catmull-Clark Subdivision Surfaces"

ディスプレイメントの微分の例
C^2連続性、二次微分の活用に関しては下記の文献、動画を参考にしていただきたい。
<参考>
"Analytic Displacement Mapping using Hardware Tessellation" by Matthias Nießner(University of Erlangen-Nuremberg)and Charles Loop(Microsoft Research)
<参考>
"Real-Time Deformation of Subdivision Surfaces from Object Collisions"
Real-Time Deformation of Subdivision Surfaces from Object Collisions
<3>レイトレースによるサブディビジョンサーフェス
続いては、DeNA/松岡 徹氏の講演について。まずはじめに、レイトレースによるサブディビジョンサーフェスのレンダリングに関して、説明が行われた。
現在レイトレーシングの主流となっているのは、サブディビジョンサーフェスではなく事前テッセレーションである。ラスタライズとのちがいとしては、2次レイトレーシングのためにテセレーション結果を残さないというもの、またメモリ消費が問題となっている。Embreeでは効率的なキャッシュが導入され、インタラクティブレイトレーシングが実現した。
<参考>
"Efficient Ray Tracing of Subdivision Surfaces using Tessellation Caching" by Carsten Benthin et al.

講演を行う松岡 徹氏(DeNA)エンジニア
そもそも事前テッセレーションは必要なのかということに関しては、二次レイトレーシングに必要な分割精度が予測しにくいなど問題点もある。直接レンダリングとなった場合、サブディビジョンサーフェス(Catmull-Clark)はBスプラインパッチに変換して使用することが可能である。
Bスプラインパッチの交差判定としては、ニュートン法とベジェクリッピング法の二通りがあり、ベジェクリッピング法に関しては、メモリ消費を抑えながらリミットサーフェスを評価することができる。ベジェクリッピング法とはBezier曲線の凸包の性質を利用して直線と曲線との交点を求める方法で、元々Bezier曲面のレイトレーシング法のために開発されたものである。
<参考>
"Ray tracing trimmed rational surface patches"
"Curve intersection using Bézier clipping" by T.W. Sederberg∗∗, T. Nishita∗
また、特徴適応分割したBスプラインバッチを使用することでセミクリースなどを少ないパッチで描画することが可能となり、結果としてこちらもメモリ消費を抑えることができる。
以上のように、サブディビジョンサーフェスとは、曲面を描画するための表現方法のひとつであるが、ディスプレイスメントでディティールを作ることができ、またC^2連続な二次微分を解析的に求められ、様々な応用が可能となる技術である。
解像度はフリーであり、ハイエンド・ローエンドで共通データを持つことやレンダリング用と3Dプリント用で共通データを持つことも可能である。事前テッセレーションに比べメモリ効率がよく、レイトレーシングにも向いている。
マシンラーニングにも適しており、この先のハイエンドゲームやコンテンツの開発などに活かされていくだろう。松岡氏は、これが主流となるとデザイナーにも数学的知識が必要となり、そこが開発のネックとなってしまう危惧があるが、そうならないようツールの開発を手伝いたいとも述べていた。
TEXT & PHOTO_遊佐怜子(FLAME)