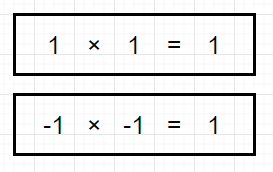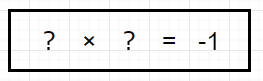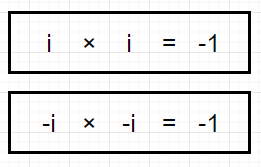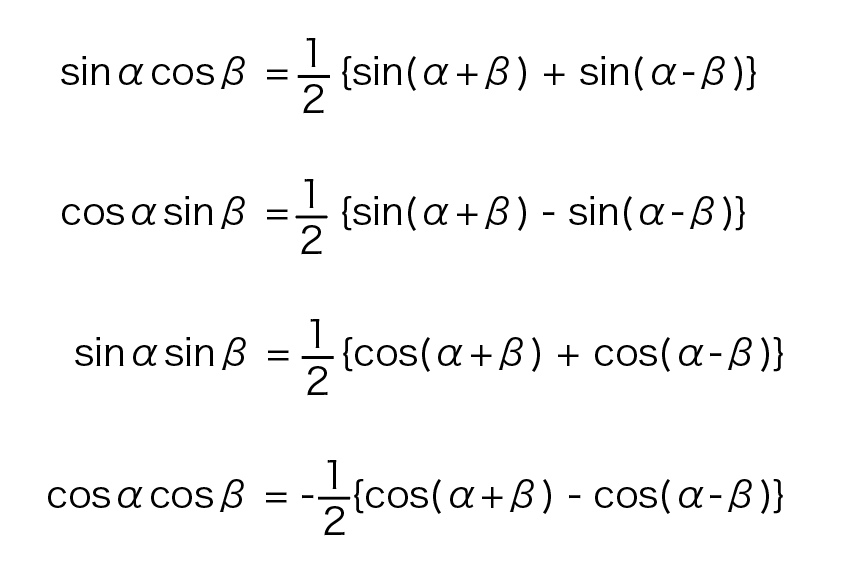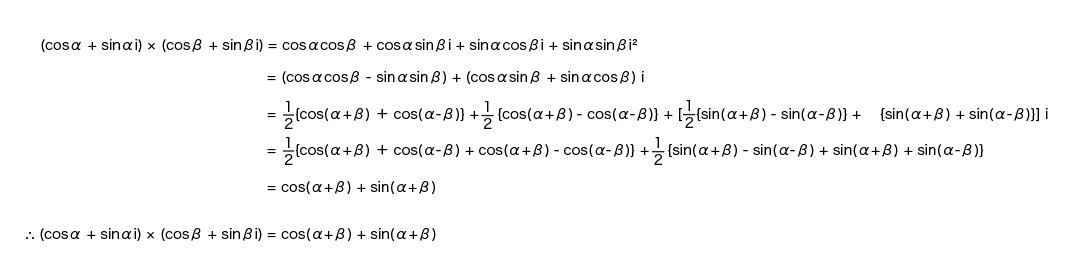おまけ:なぜQuaternionはかけ算で回転加算になるのか?
Quaternionの回転計算について少し踏み込んだおまけです。
そもそも、どうしてQuaternionはかけ算で回転加算になるのでしょう。
なぜ足し算ではだめなのでしょうか?
これは、
「厳密にいうと、Quaternionをかけ算すると回転になる」
というよりも、
「Quaternionのかけ算で回転を表現できるので便利」
という認識のほうが正しいかもしれません。
でも別に、ここを深く理解せず「そういうものだから!」で飲み込んで先に進んでもまったく問題ないと思います。いわゆる「公式」のように認識して、どんどん先に進むべきです。
しかし、ここを理解した上で飲み込みたい人もいるはず。 ですので、ほんの少し深掘りしてみましょう。
Point 01:Quaternion=四元数は複素数の拡張
先に述べたように、Quaternionは複素数を拡張した概念です。ここでは複素数のかけ算を例として紹介し、Quaternionがなぜかけ算で回転加算になるのかの理解へつなげたいと思います。
Point 02:複素数は想像上の数(かず)!
まず初めに、二乗して1になる数値って何でしょうか。
答えは、1と-1ですね。
では、二乗して-1になる数値は?
答えは、自然界には存在しないということになっています。
でも、昔の数学者の人たちは考えました。
「もし二乗したら-1になる数値が存在したら...?」
数学者は、この想像上の値=「Imaginary number」を、頭文字「i」を取って数式上表すことにしました。これが虚数です。
では、自然界に存在する数(かず)=実数と虚数を足し算したらどうなるでしょう?
その数値は交わることができないので、このように「実部」と「虚部」をもつかたちで表すことができます。この実数と虚数を足した値を「Complex number」、すなわち「複素数」と呼びます。
Point 03:複素数を平面上に表してみよう
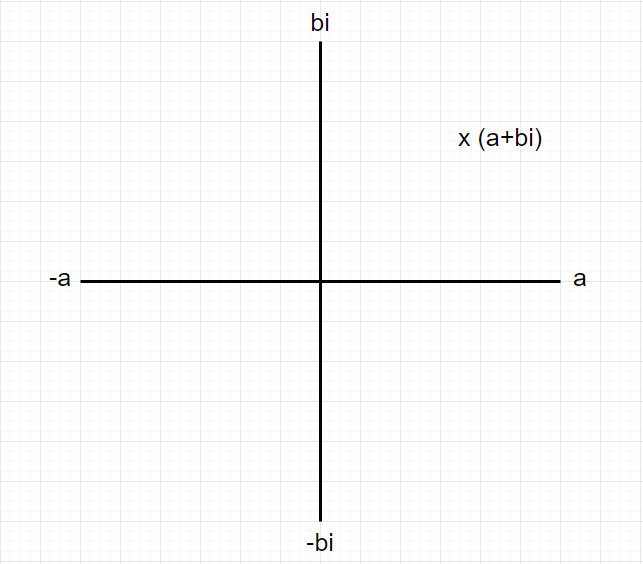
縦軸を虚部、横軸を実部とした平面を作って、2次元的な側面で複素数を考えてみたらどうなるでしょう?
複素数(a+bi)は上記のように表すことができます。
このような複素数を表す平面を「複素数平面」と呼びます。
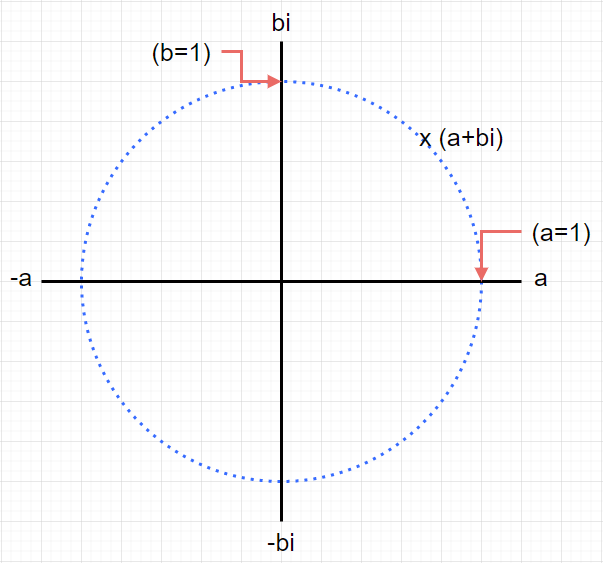
ここに、原点から半径1の単位円を重ねてみると、こんな風になりました。
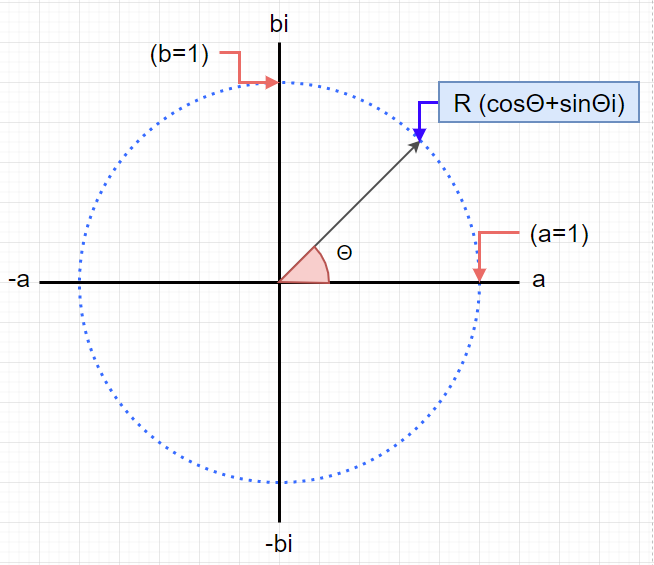
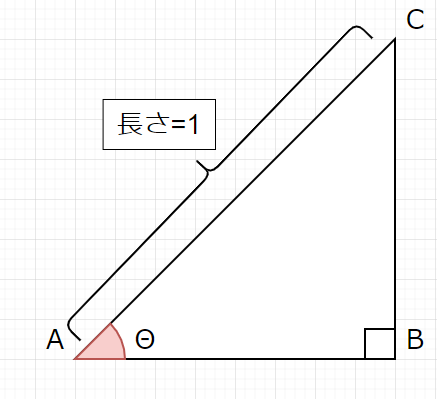
円Oは半径1の単位円なので、円周上の点Rはこんな風に表すことができます。
上記は長辺1の直角三角形に対する三角関数で計算することができます。
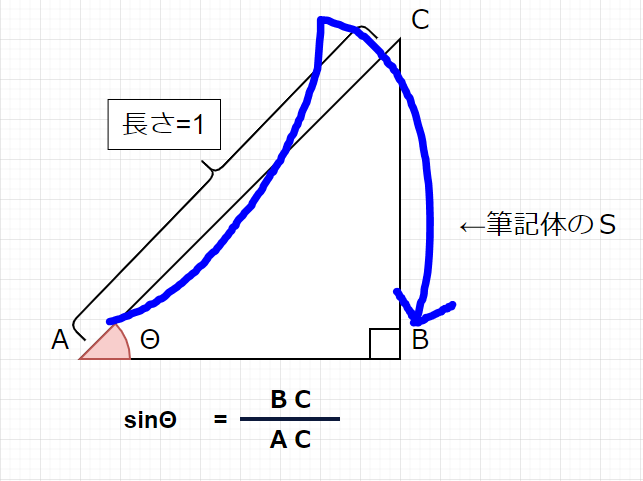
上記の三角形での辺BCの長さはsinΘで表すことができるし、
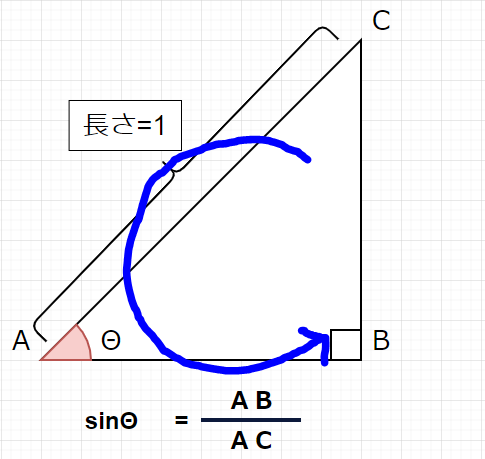
辺ABの長さは同様にcosΘで表すことができます。
上記のような「覚え方」の図は、高校数学の授業で出てきたのではないでしょうか。筆者はいまだにこの図を使っています。
Point 04:複素数のかけ算を複素数平面で2次元的に考えてみると......?
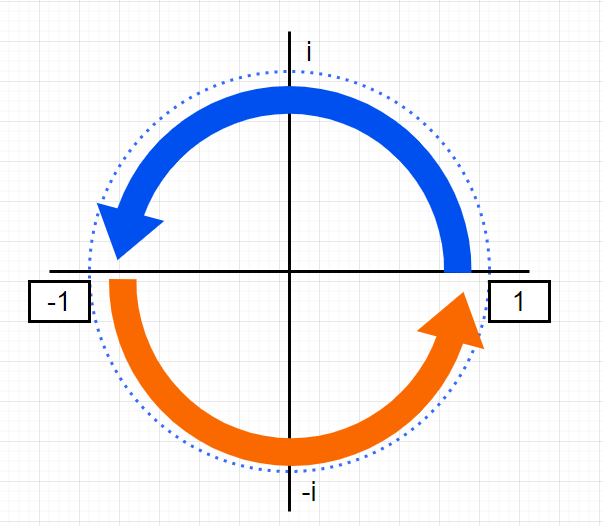
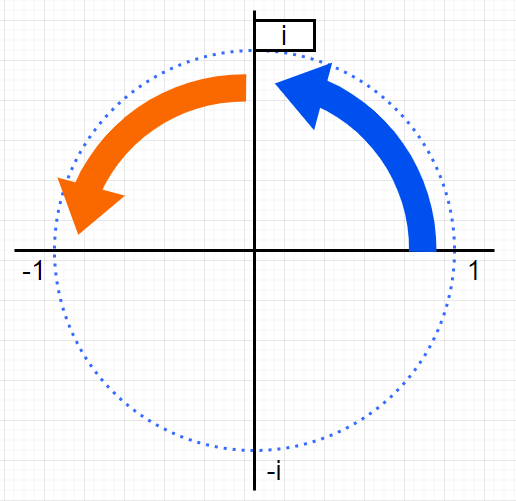
先ほど出てきたように、-1は二乗すると、1になります。
複素数平面で考えると、こうです。
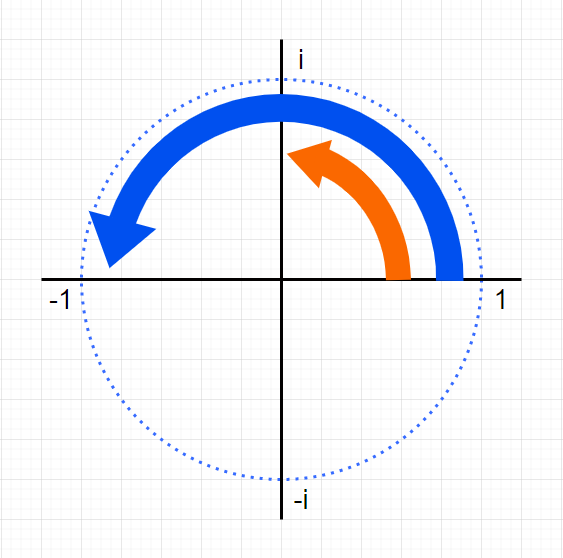
では、iを二乗すると?
-1なので複素数平面上ではこうです。
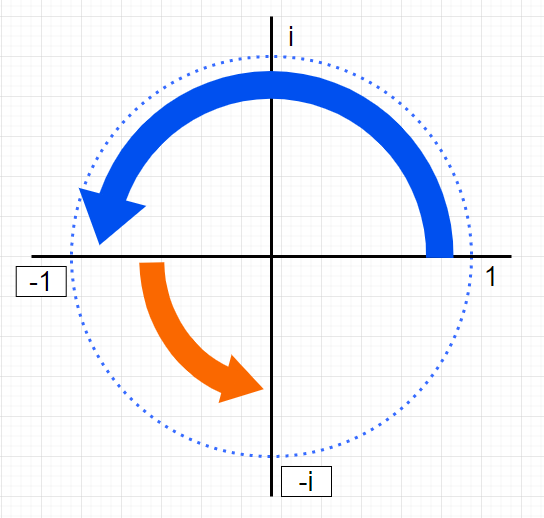
では-1にiをかけると?
-iになります。
ここで気づくべきは、複素数平面上で見ると、複素数のかけ算は回転加算になっているように見える......ということなのです。
果たして本当にそうでしょうか?
Point 05:複素数のかけ算の式を展開して考えてみる
上記のように、複素数のかけ算が回転加算になっているのだとすると、
(cosα + sinαi)×(cosβ + sinβi)
は
cos(α+β) + sin(α+β)i
になるはずですよね。
では、
(cosα+sinαi)×(cosβ+sinβi)
を展開してみましょう。
ここでは、三角関数の積和の公式を使って式を展開します。
●積和の公式
●式の展開
ほらね!!
このように、複素数平面において、単位円上にある複素数同士のかけ算
(cosα+sinαi)×(cosβ+sinβi)
は、(cosα+sinαi) の角度αをβ分追加回転させたことに等しい、と言えるわけです。
つまり言い換えると、
複素数のかけ算で回転が表現できる
ということになるのです。
以上はあくまで2次元上の計算でしたが、これを立体で考えられるよう拡張されたのが四元数、すなわちQuaternionになります。
数学って意外とグラフィカルな側面がありますね!
いかがでしょうか!
以上で示した通り、複雑な回転制御でも回転成分を分解して考えることでシンプルな実装が可能になります。
また、補助骨制御におけるオイラー回転の導入がリスキーであることも一部紹介いたしました。もちろんオイラー回転が全てNGなわけではないと思いますので、導入の際は用途をよく考えて設計すると良いでしょう。
さらにおまけでは、なぜQuaternionはかけ算で回転加算になるのか少しだけ追究してみましたが、数学のグラフィカルな面に触れられたのではないでしょうか。
次回は「ベクトルの活用(内積・外積・三角関数)」と称して、この数学のグラフィカルな面にアプローチしていきたいと思います。
いやー、リギングってホントに面白いものですね!
では今回はこの辺で!
サヨナラ!サヨナラ!サヨナラ!!
Profile.
-

-
山本智人/Tomohito Yamamoto(COYOTE 3DCG STUDIO)
ゲーム開発会社にてグラフィックアーティストとして、モデリング・モーション・エフェクト・UIなどオールラウンドのグラフィック制作を経験後、テクニカルアーティストに転身。現在は株式会社クリーク・アンド・リバー社 COYOTE 3DCG STUDIOにて、社内外問わずアーティストのDCCツールサポートや制作パイプラインの提案・作成・運用を行う。特にアニメーション制御やモーション制作周りのテクニカルサポート・リガーとして様々なプロジェクトに従事