2024年11月18日（月）から22日（金）まで、日本最大級のCGカンファレンス「CGWORLD 2024 クリエイティブカンファレンス」がオンラインで開催された。22日（金）には、「つくって学ぶ 機械学習きほんの「き」Sponsored by SideFX」が実施され、SideFX Houdini Senseiのさつき先生氏が登壇。Houdiniで簡単なAIを作成して基本を学び、手書き文字を認識させるまでの手順が解説された。

＜1＞機械学習とは？

本セッションの講師を務めたのは、SideFXのさつき先生。Houdiniに関する講義やチュートリアルの制作を行なっており、「Houdini Sensei」という肩書きが正式に名刺にも記載されているという。

まず「機械学習とは何か？」という問いに対し、ChatGPTに尋ねたところ、次のような回答が得られた。

「機械学習は、データから学び、予測やパターン認識を行う力を与えるものです。それはまるでコンピュータが、データという経験から知識を得て、世界を理解する方法を発見していくようなものです」

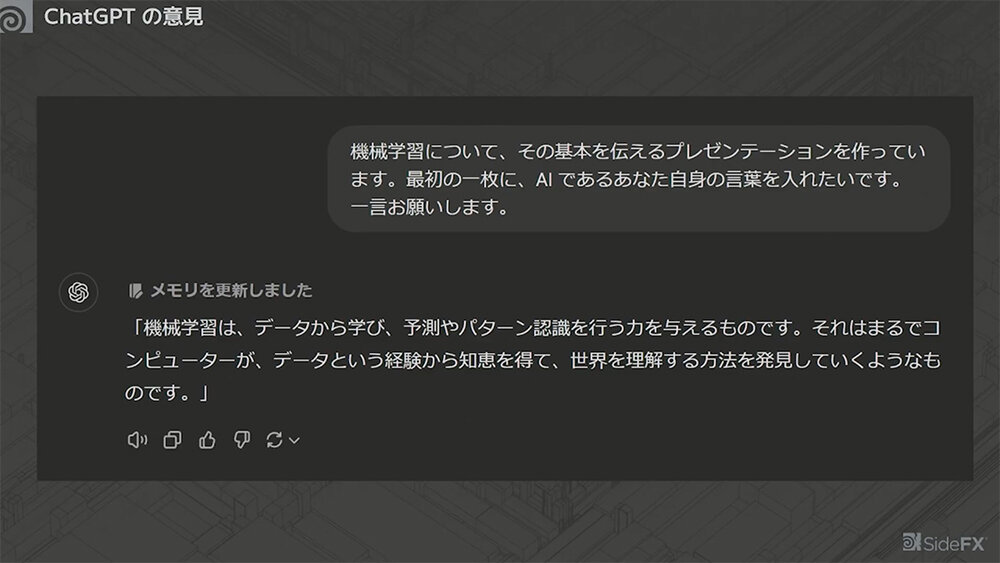
この説明を受け、さつき先生は「確かに世の中では機械学習がこのように説明されることが多い」としつつも、具体性に欠けるため、次のような疑問が生じると指摘した。

・どうやって「予測」するのか？
・「学ぶ」とは具体的にどういうことか？
・「世界を理解する」とは何を意味するのか？

こうした曖昧な説明ではなく、「自ら手を動かしてイチから機械学習のしくみを理解すること」が本セッションの目的であると、さつき先生は強調。続けて、「りんごとみかんを色で判別するには？」というシンプルな課題を用いて、機械学習の基本概念を紐解いていった。

＜2＞りんごとみかんを色で判別するには？

単に直線で分ける方法

まずは、直線を使って分類する方法について説明する。色をRGBの値で表し、それぞれをXYZ軸に対応させると、カラースペース上にキューブができる。

一般的に、りんごは赤色、みかんはオレンジ色であるため、識別にほとんど影響しない B（ブルー）の軸を削り、2次元で扱う。実際の機械学習でも、不要な情報を削減するために高次元のデータを低次元に圧縮する手法が用いられている。

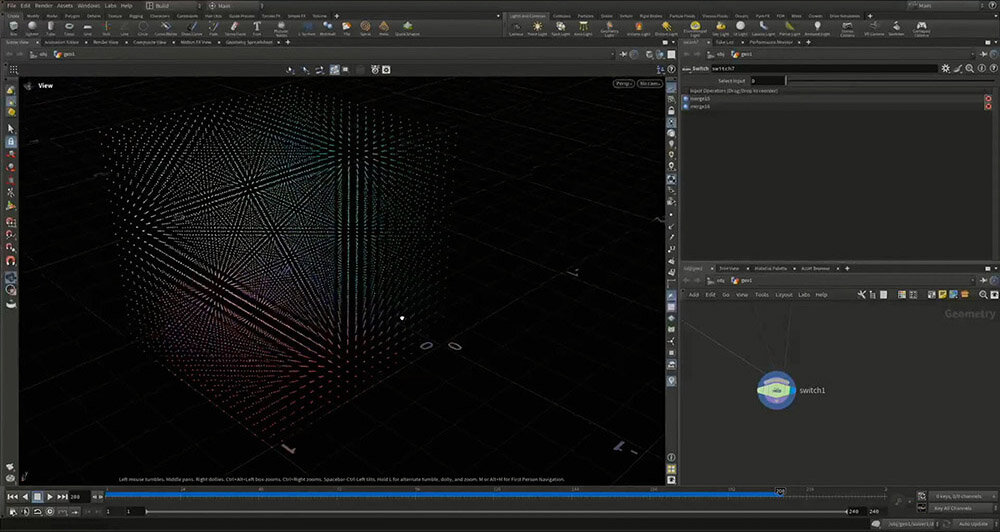
このようにして、データを2次元に圧縮すると、大まかに赤色（りんご）とオレンジ色（みかん）に分布する。

ここで、りんごかみかんかを機械に判断させるためのシンプルな指標として、y=ax+bで表される直線を利用できる。この直線の位置を調整することで、様々な分類境界を引くことが可能になる。

RGBのデータからR（レッド）とG（グリーン）の2次元空間に変換し、不等式を用いることで分類を行う。この例では、直線より上の領域をみかん、下の領域をりんごと判別する。

この方法を整理すると、以下のようになる。

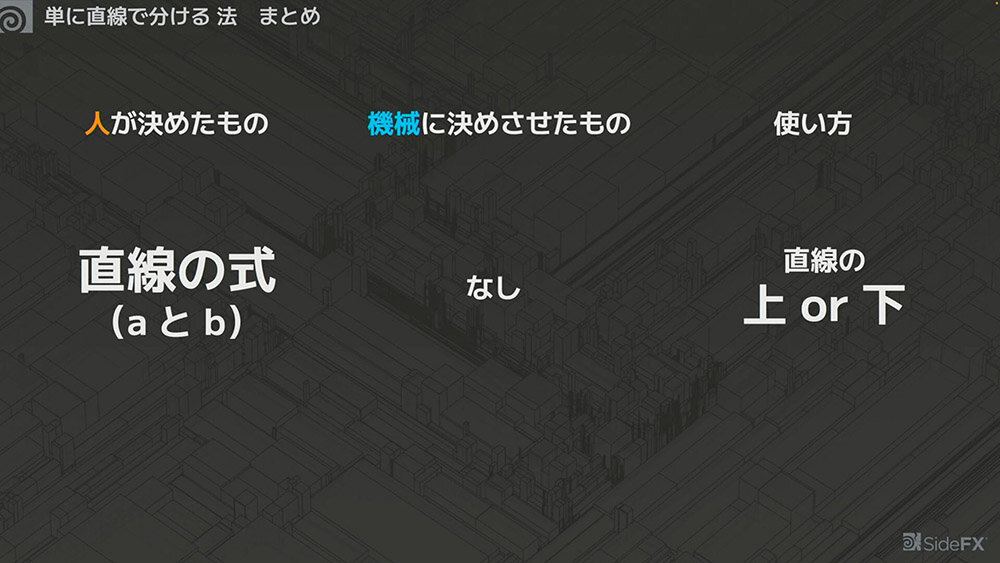
ここで重要なのは、判別に「直線を使う」という選択自体が人が決めたものであることだ。その上で、パラメータ（aとb）も人（さつき先生）が決めている。

一見すると当たり前のことのように思えるが、この考え方は今後の機械学習を理解する上で非常に重要になるため、ぜひ覚えておいてほしいとのこと。

k-means法で分ける方法

りんごとみかんに青りんごを追加すると、RGBのデータを用いて色を判別しようとしても、直線だけでは分類できなくなる。そこで、別の方法を考える必要がある。ここで登場するのがk-means法だ。

k-means法の「k」は何らかの定数を指し、「means」は足して平均を取ることを意味する。りんご、みかん、青りんごのRGBデータは、人間の目で見れば容易に識別できるが、機械にどのように分類させるかを決める必要がある。

ここでは、さつき先生が3つの核（クラスタの中心）を手動で設定し、それぞれの色データと核を線で結ぶことで、最も近い核を探し出すようにした。

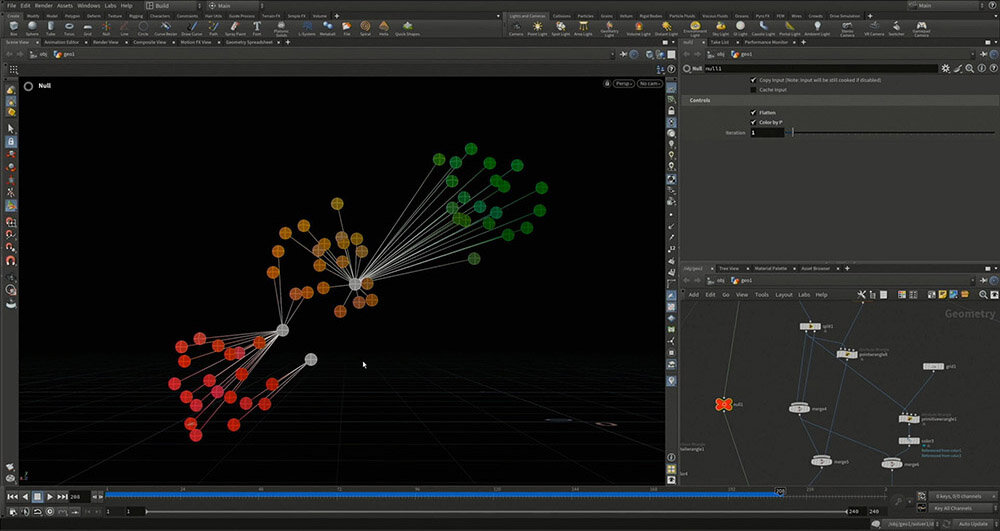
次に、Houdiniのイテレーションの値を変えることで、平均値の位置を探しながら核を移動させる。このプロセスを何度かくり返し、核が適切な位置に分布すると、最終的に収束し、動かなくなる。このようにしてデータを分類するのがk-means法のアルゴリズムである。

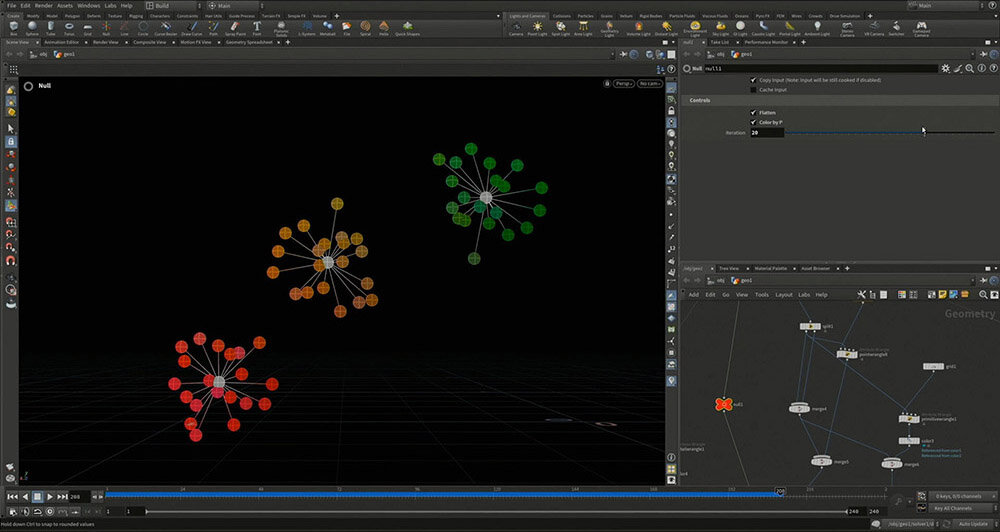
続いて、核ではなく、空間全体に注目してみる。すると、どの位置にあれば、どの色に分類されるのかを視覚化できる。例えば、下の図では右上のグループ（青りんご）に分類されるものは、紫色のエリアに入っていることになる。

k-means法をまとめると、以下のようになる。

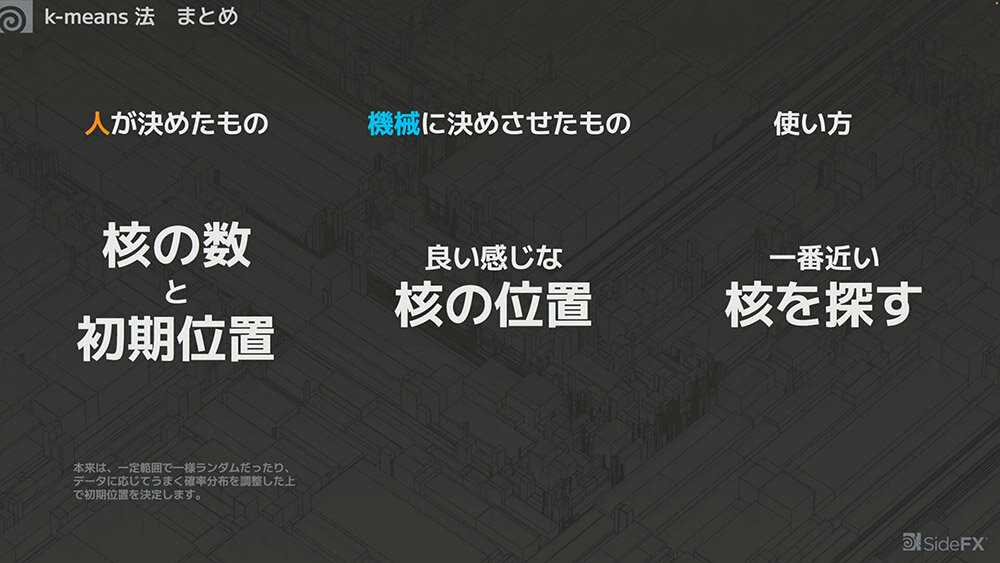
本来、初期位置は一定範囲内でランダムに配置する、あるいはデータに応じて確率分布を調整するなどの手法で決定されるが、ここでは人が手動で設定している。

k-means法のアルゴリズムに従い、核の位置を少しずつ移動させ、収束した結果を最終的な位置として機械が採用する。このように、ボロノイ図のように一番近い核を探す手法を用いることで、単純な直線による分類とは異なり、より柔軟で複雑な区切り方が可能になる。

これでようやく、機械学習の形になってきた。機械学習における「学習」とは、様々なルールに従い、機械に決定を委ねることを指す。「アルゴリズムなどを用いて機械がデータを調整するプロセス全般を、ざっくりと「学習」と呼ぶイメージで構いません」（さつき先生）。

＜3＞ニューラルネットワーク〜巨大な計算グラフ

ここから、機械学習の本題に入る。直線やk-means法に比べ、より汎用性が高いのがニューラルネットワークだ。

「ニューラルネットワークとは何のネットワークなのかというと、ただの計算グラフのことを言っています。Houdiniユーザーの方はVOP Networkというノードベースで計算を行うコンテキストがあるので、それを思い浮かべるとわかりやすいと思います」。ここではインプットとしてRとGが入力される。ニューラルネットの内部で何らかの「スゴい計算」が行われるとして、その結果をアウトプットする。

まずは青りんごを除外し、りんごとみかんの判別に限定すると、アウトプットは2種類となる。それぞれの値を比較し、より大きい方の値に応じて「りんご」または「みかん」と判定するしくみになっている。

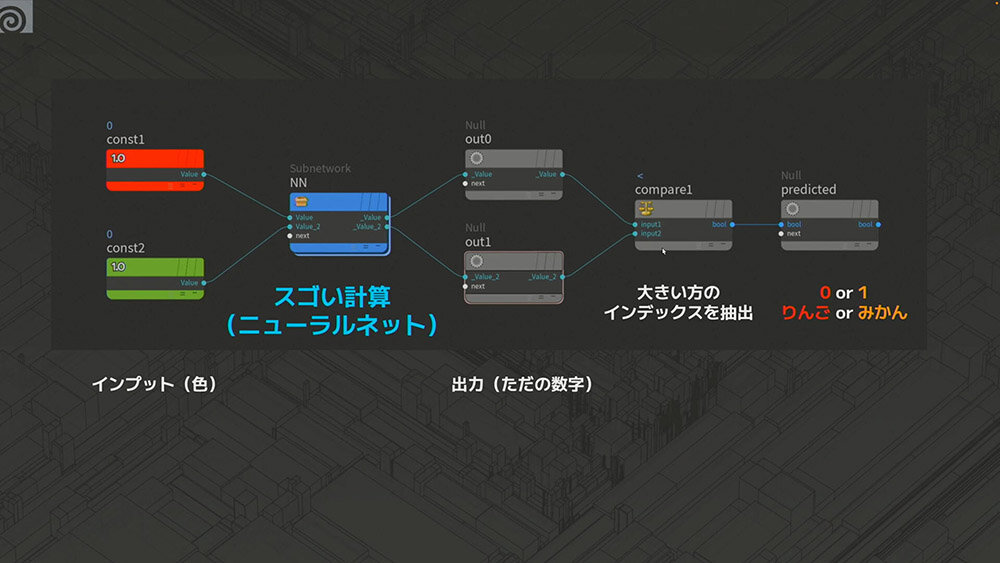
りんごとみかんに青りんごが加わったとしても、アウトプットが3つになるだけで基本的な考え方は変わらない。「最大のもののインデックスはどれか？」という計算をサブネットで行い、最も大きな値をもつインデックスを予測結果として取得する。

インプットの数が増えても計算の方法は同じで、最終的に手書き文字認識のようなタスクでは、例えば28×28＝784個のインプットから10個のアウトプットを計算することになる。

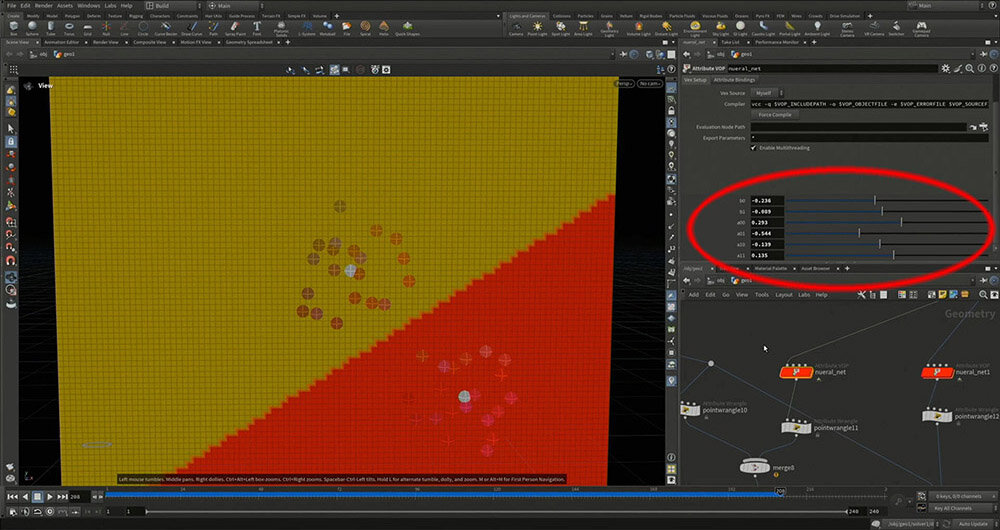
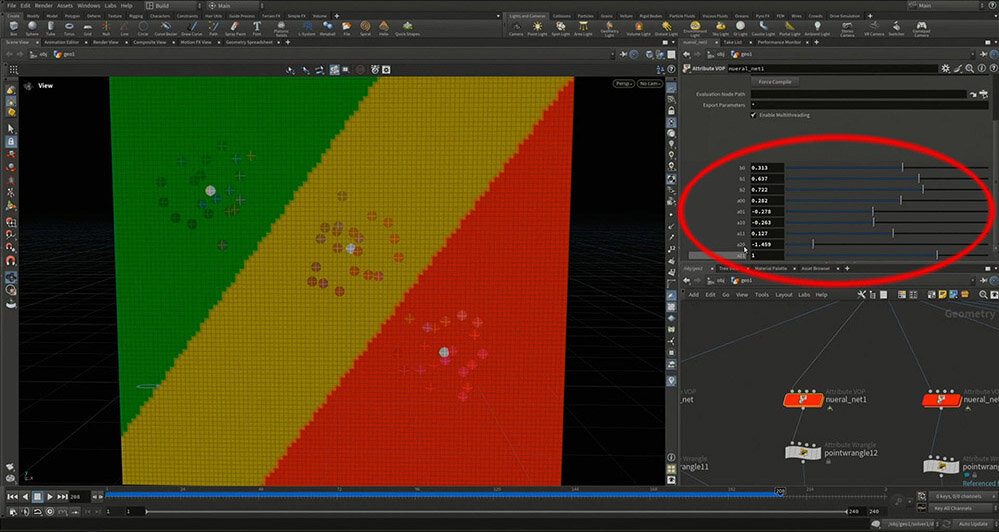
問題は、ニューラルネットワークの内部がどのように処理を行なっているのか？ という点だ。ここでは、インプットとしてRとGの情報を位置のX軸とY軸にプロットし、「スゴい計算」を通じて最大のインデックスを導き出す様子がHoudini上で解説された。この計算はノードによって構成された数式として表現される。

各色の情報を活用しながら計算を行い、最終的な調整を施すことで、それぞれのアウトプットがインプットの情報を使いつつ、可能な限り単純な式になるように設計されている。

調整可能なパラメータの数を計算すると、インプットが2つ、アウトプットが2つあるため 2✕2＝4、さらに各出力を調整するためのパラメータが1つずつあるので 4＋2＝6。つまり、合計6個のパラメータが表示されることになる。

ニューラルネットワークでは、青りんごが増えてもインプットの数は変わらず、RとGの2つのままである。処理の流れもりんごとみかんの分類と同じ種類の計算を行い、アウトプットを3つつくるという点で変わらない。

インプットが2つあるため、3×2＝6。さらに、各出力を調整するためのパラメータが1つずつあるため、6＋3＝9。つまり、合計9個のパラメータが表示されることになる。

つまり、ニューラルネットワークといっても、基本的にはただの関数であり、極めて膨大な計算をしているものの、根本的な構造はシンプルな計算の積み重ねである。

ここで重要なのは、各アウトプットをつくる際に、インプットの情報を全て活用するように設計されているという点だ。

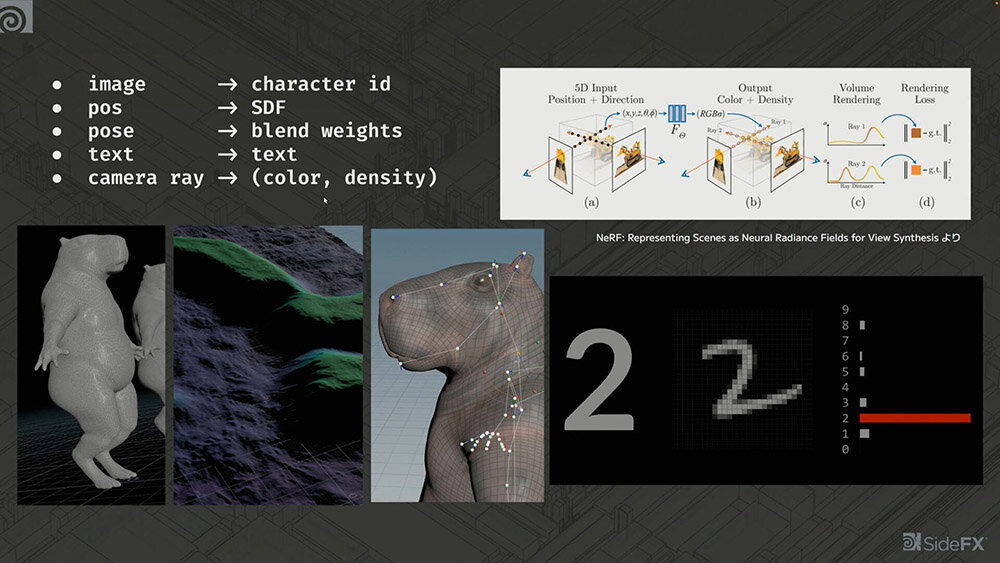
りんご、みかん、青りんごを分類する簡単な例を示したが、この考え方は様々な分野に応用できる。

例えば、手書き文字認識では、画像をインプットとして文字のIDをアウトプットするが、その計算をニューラルネットワークで行なっている。同じように、SDF（Signed Distance Field）、翻訳、さらにはChatGPTのような大規模なモデルにまで応用が可能である。

＜4＞別世界のりんご〜非線形な世界〜

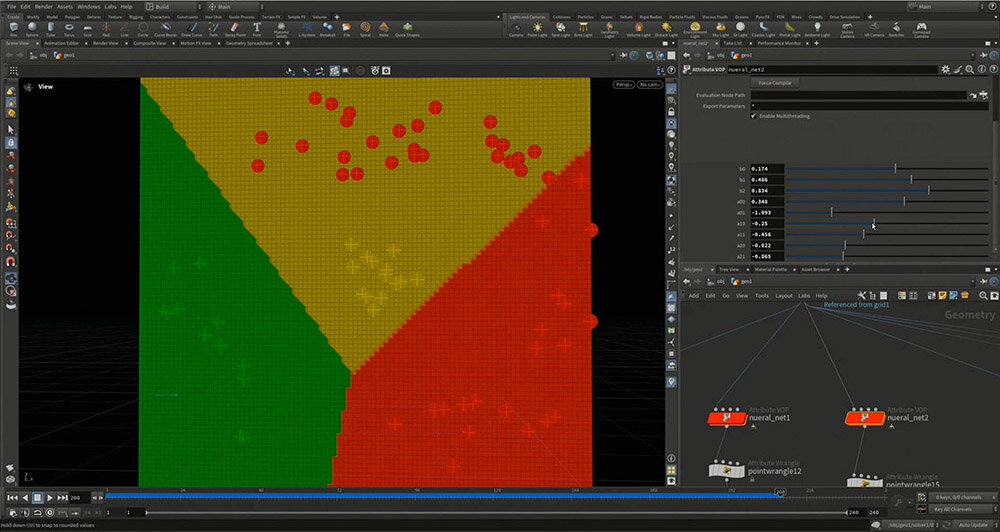
これまでのりんご、みかん、青りんごを分類する話だけなら、k-means法で十分ではないか？ と思うかもしれない。しかし、ここで「別世界のりんご」と題された下図のような例が提示された。

このような分布では、直線を使った分類が不可能になってしまう。

先ほど使用したノードをコピーしてそのまま適用しても、3つをきれいに分類することはできない。そのため、非線形の世界が必要となり、直線ではなく折れ曲がる線を用いる必要がある。

ここで必要になるのがMAX関数だ。MAX関数は、2つの入力がある場合に最大値を出力するため、0とのMAXを取ることで処理を工夫できる。つまり、負の値を入力すると出力は0になる。この処理は正規化線形関数（Rectified linear function）、それを利用したユニットとしてReLU（Rectified Linear Unit）関数とも呼ばれている。

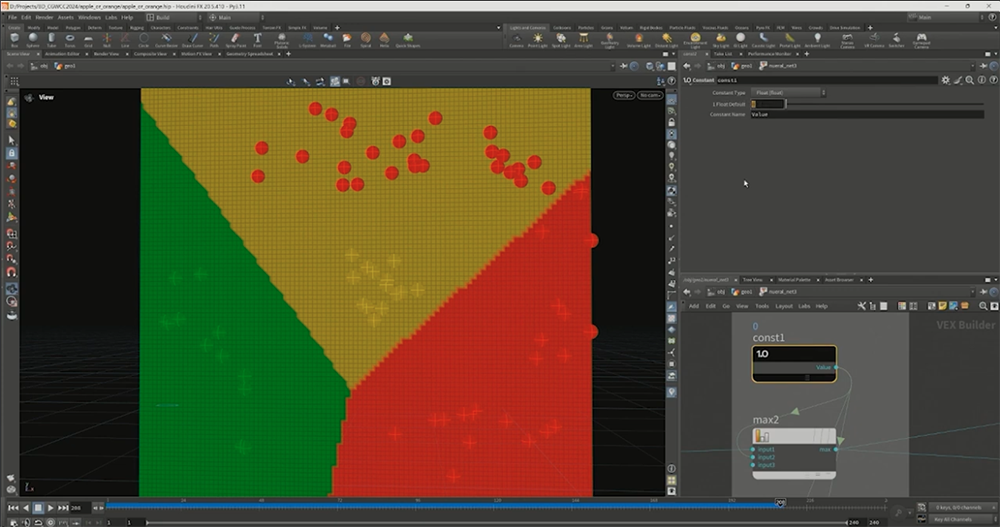
例えば、y = x のグラフでMAXを取ると、直線ではなく、以下のような非線形な形状になる。

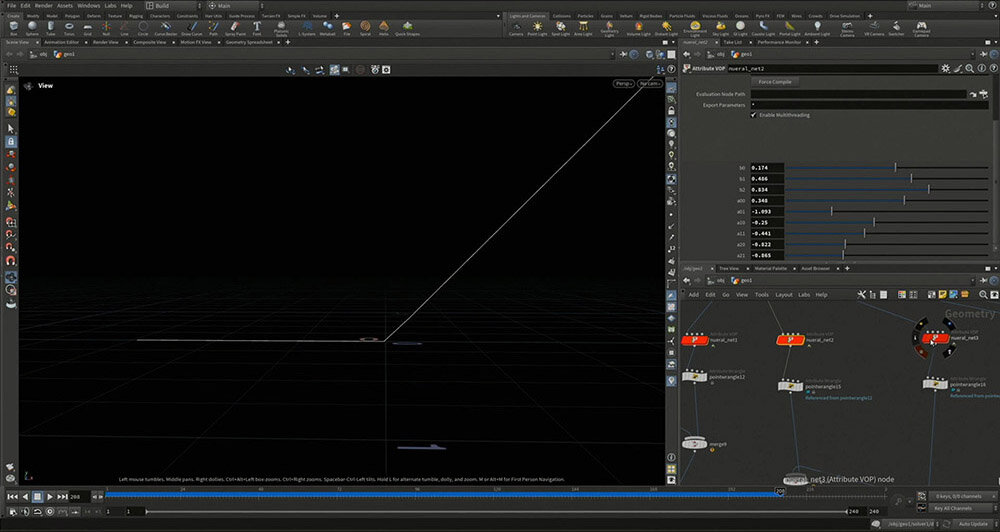
「別世界のりんご」の例でも、それぞれのアウトプットにMAX関数を適用することで、分類の境界線が折れ曲がり、3つをきれいに分けることができる。

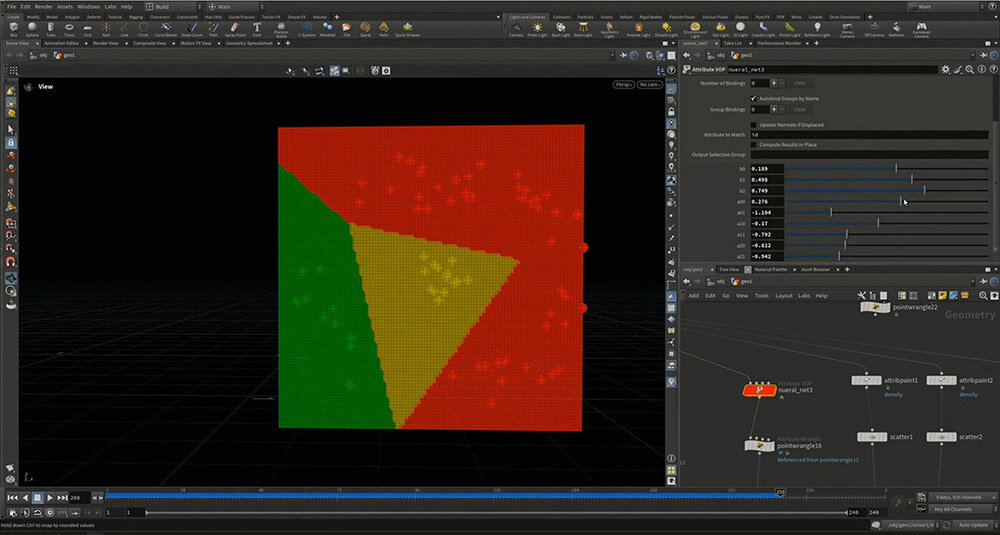
ここまでの説明を踏まえ、ニューラルネットワークのしくみを整理すると、以下のようになる。

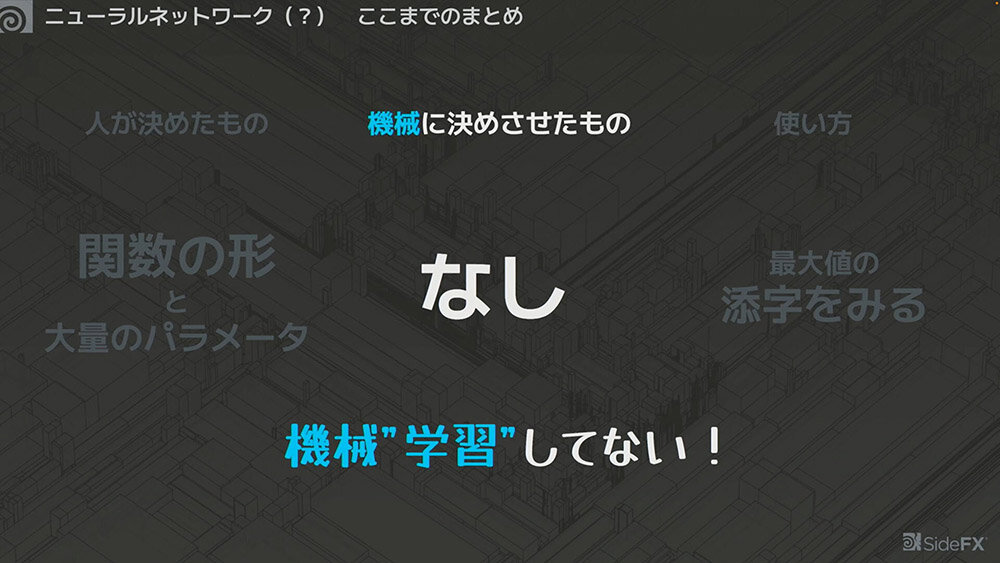
関数の形は、全てのインプットにウェイトを付けて足し合わせ、MAX関数を挟むというもの。その上で、さつき先生がパラメータの値を調整した。

使い方としては、値そのものではなくインデックスを確認し、どの値が最も大きかったかを判断する。

ただし、現時点では機械に決めさせたものが「なし」となっており、つまり、まだ機械学習をしていない状態と言える。ここから、機械が自動的に最適な値を調整し、「良い感じ」に寄せていく方法が説明された。

＜5＞損失関数の導入

この「良い感じ」を数値化した指標が「認識精度」である。しかし、認識精度の変化はわかりにくい。多少パラメータを調整しても、大抵の場合、認識精度にはほとんど変化が見られない。

そのため、どのように変化させるべきかを判断しやすくするために、別の指標として「交差エントロピー誤差」と「二乗和誤差」を導入する。どちらも、「正解に近いほど0に近づく」という特徴をもつ点が重要である。

この指標は「損失関数」とも呼ばれ、損失関数の値が小さくなるようにパラメータを調整していく。

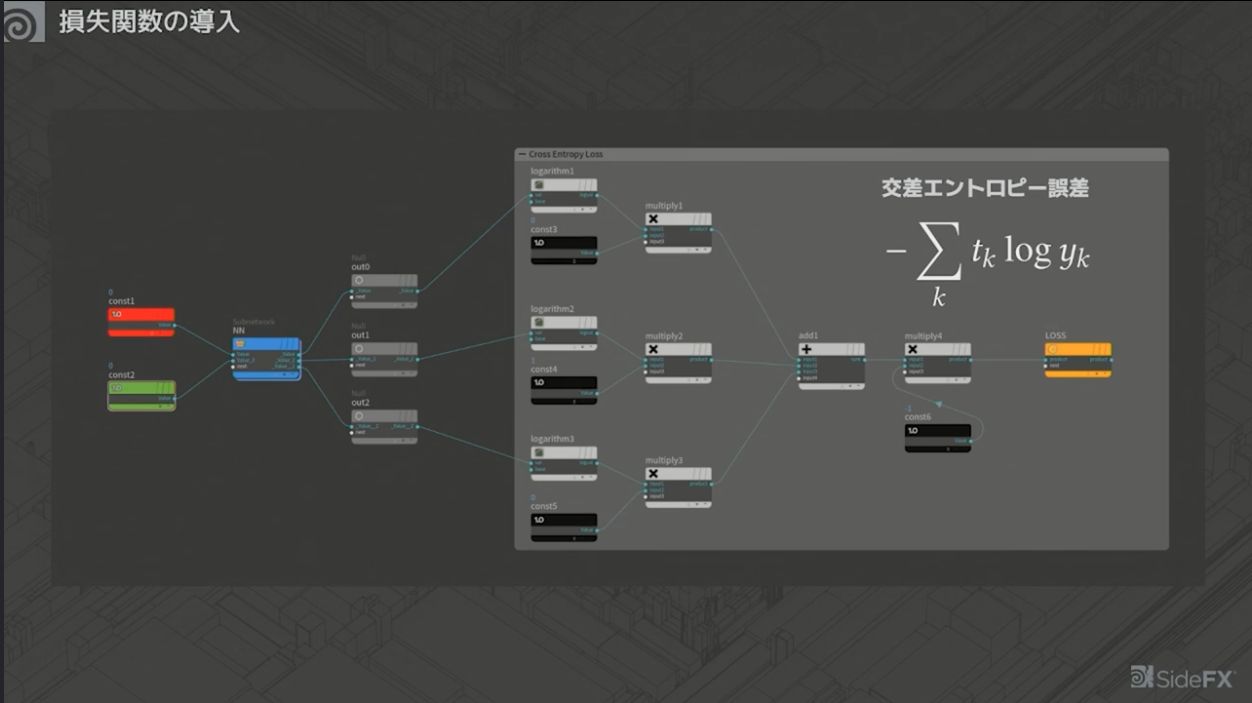
しかし、どのようにパラメータを調整すれば損失関数が小さくなるのか？ これがわからない場合は、どの方向に動けば損失関数が減少するのかを考えることが重要になる。

損失関数は、2次元の入力に対して1次元の実数として表現される。Houdiniを使って、起伏のある丘のような図を作成し、高さを損失関数と仮定する。そこにボールを置き、少しずつ低い方へ転がしていくようなイメージでパラメータを調整する。

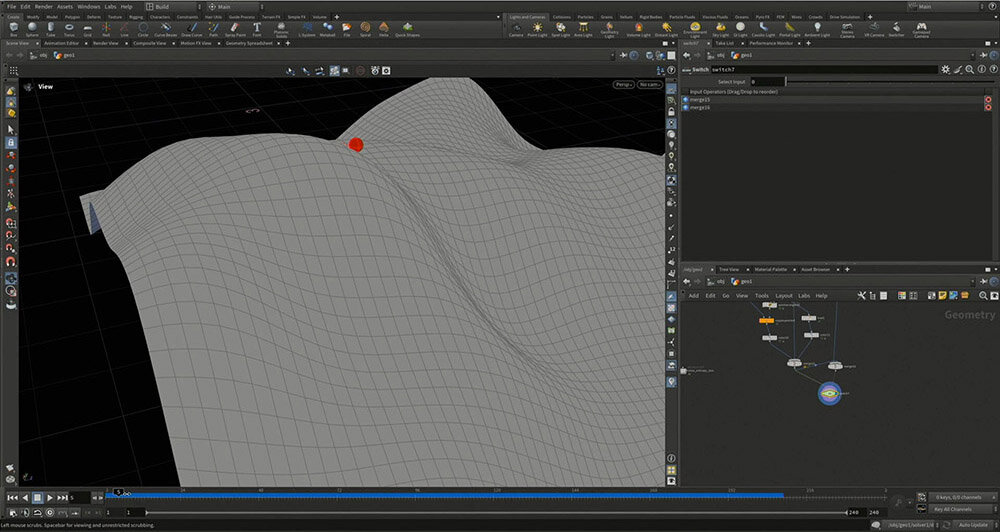
高さの値が小さい方向を探索し、その方向に少しずつずらしていくシミュレーションをくり返すと、極小の位置（高さが最も低い位置）に到達したとき、どの方向にも動けなくなる。これが学習結果である。

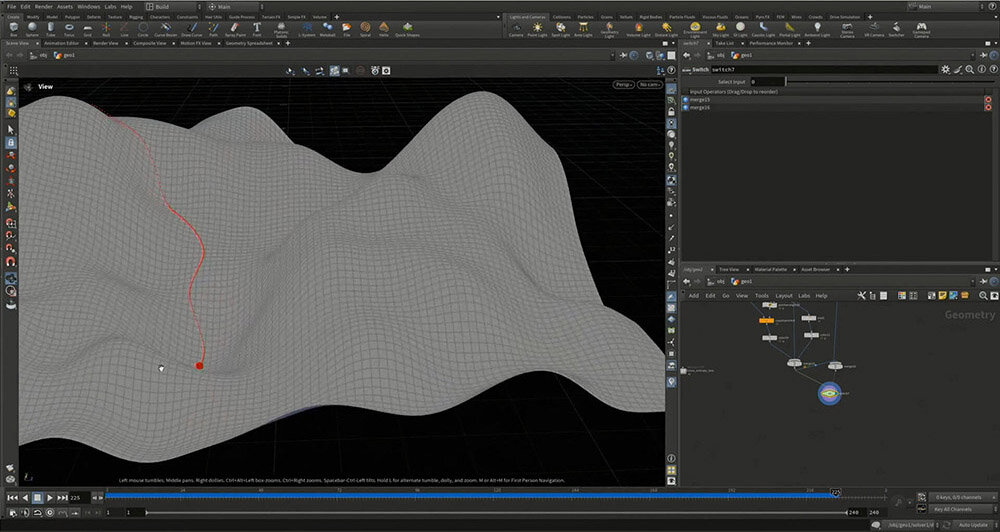
最初の位置からわずかに動かした方向と、その方向に対して直角の方向に動かした場合を比較すると、どちらに進めばよいかを計算できる。

ここでは、ボールが丘を転がり落ちる方向を調べ、低い方へ向かってパラメータを調整すれば損失関数が小さくなるという例を示した。しかし、次元が大きくなったとしても、基本的な計算方法は変わらない。

＜6＞微分

ここまでの内容を理解したうえで、次の説明に入る。ここでキーとなるのが「微分」である。

例えば、足し算の式 y=a+b において、 aを0.01だけ増やすと、yも0.01増える。このとき、変化の比率は1になる。変化量をΔで表すと、以下のように記述できる。

次はかけ算について考える。

例えば、y=a✕b の式において、 aを0.01だけ増やした場合、yの変化量は0.01bとなる。つまり、bが大きければ大きいほど、aを増やしたときのyの増加量も大きくなる。

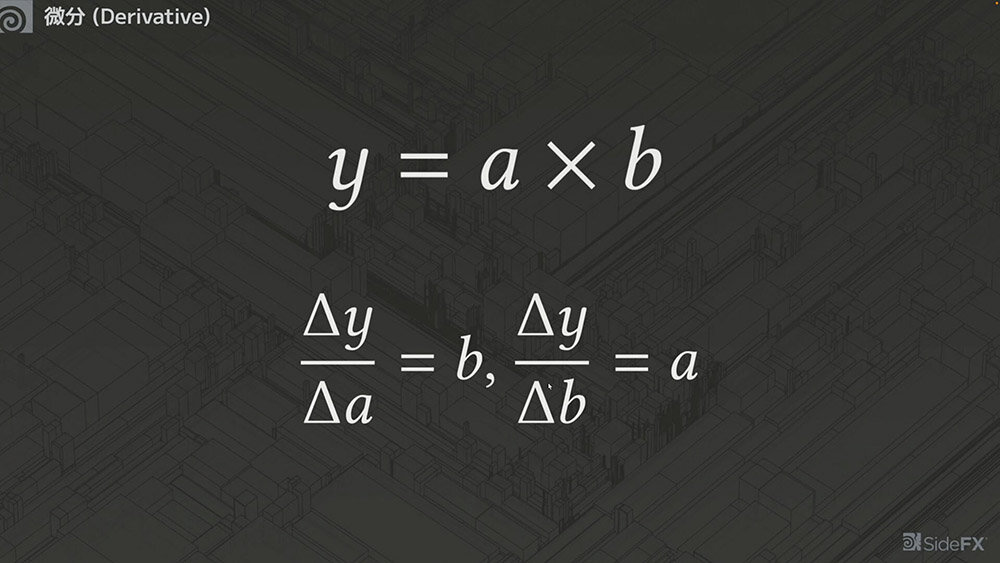
さらに、二乗の計算。aの二乗の式では、y=a✕aという式に分解できるため、 aに対してaだけ増えると考えられ、yの変化率は2aとなる。

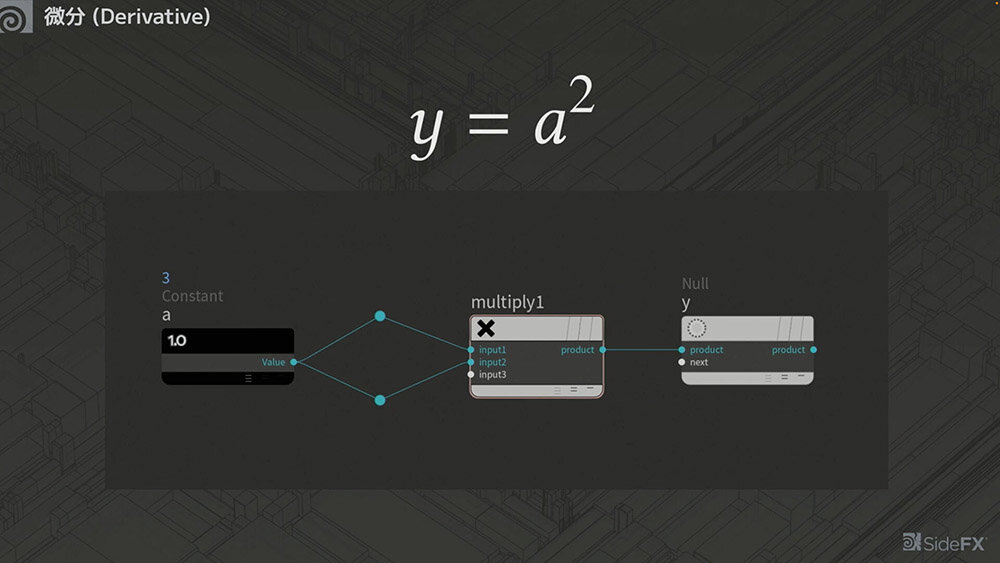
今度は、下図のような式を考えてみる。途中の数式はややこしくなるが、Δcはキャンセルされるため、最終的に2 (a+b)という形になる。

関数が複数ある場合、それぞれの間でインプットが増えたときにアウトプットがどれだけ変化するかを考えると、全てかけ合わせることでキャンセルされることがわかる。

つまり、ひとつずつローカルな値がわかっていれば、それらを繋げた全体の変化も簡単に求めることができるということだ。

ここでは足し算とかけ算のみを扱っているが、それ以外の演算でも微分は可能である。関数がどれだけ大きくなっても、隣接する値を順に求めていけばよい。これを「微分の連鎖律（Chain-Rule）」と呼ぶ。

最終的に、連鎖律を利用して巨大な関数を微分しながら、「何を変化させたらどのように動くか」をひとつずつ求め、パラメータを調整していくことになる。

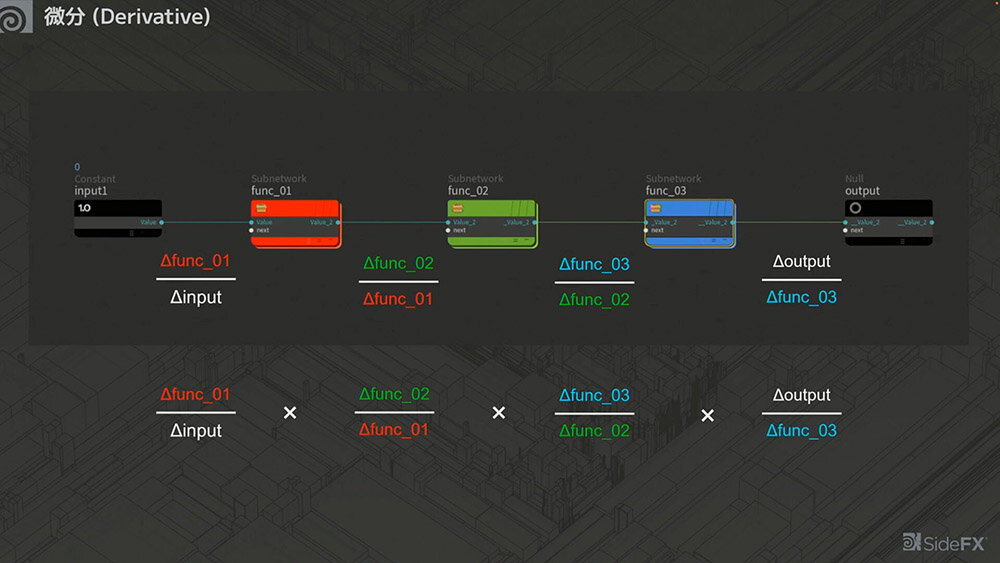
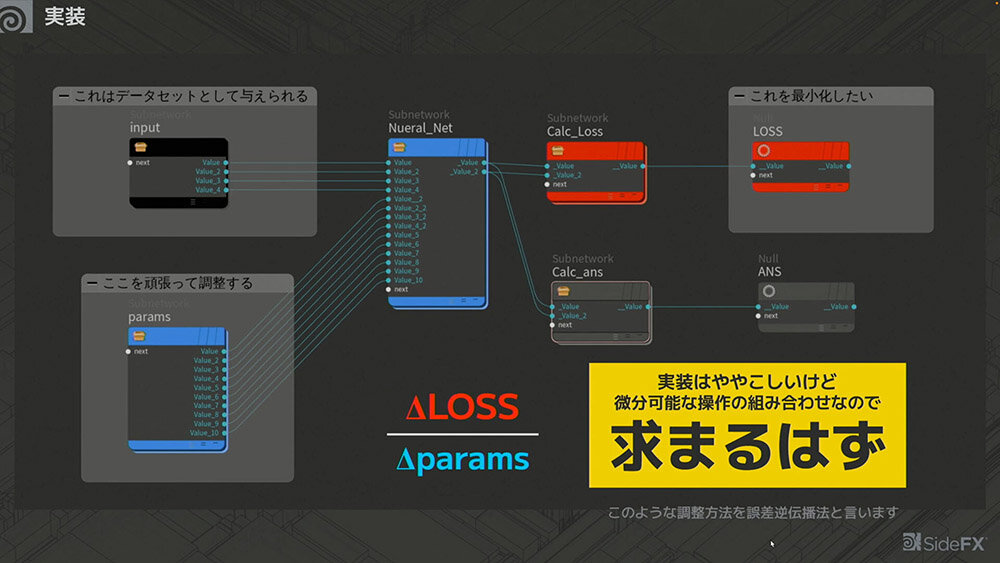
微分についてまとめると、大量のインプットとパラメータが、ニューラルネットワークという巨大な関数に入力される。この関数を計算し、最小化できれば「勝ち」 というわけだが、そのためにはパラメータを変化させたときにLOSS（損失関数）がどのように変わるかを把握することが重要となる。

実装は複雑になるものの、微分可能な操作の組み合わせによって最適な答えを導き出すことができる。

このように、後ろから微分を求めていく方法を「誤差逆伝播法（バックプロパゲーション）」と呼ぶ。

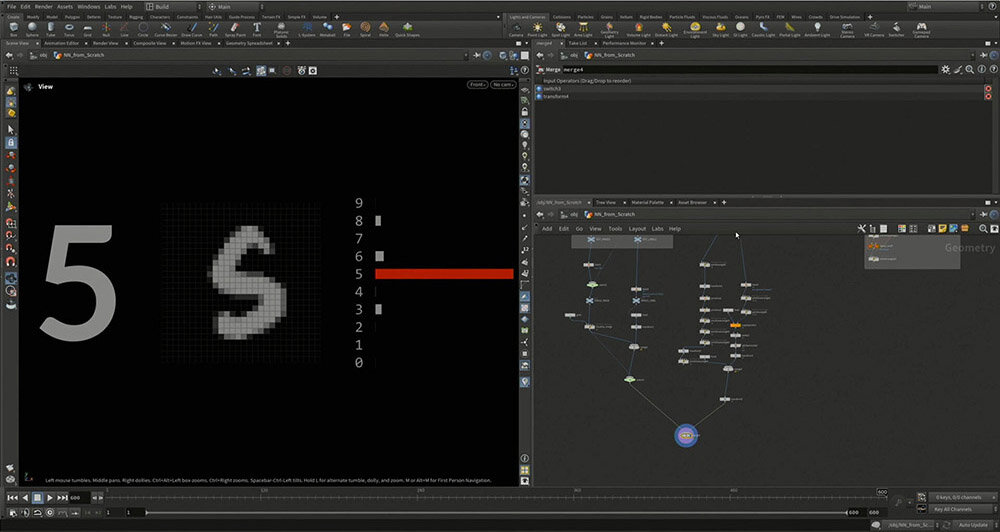
＜7＞手書き数字認識

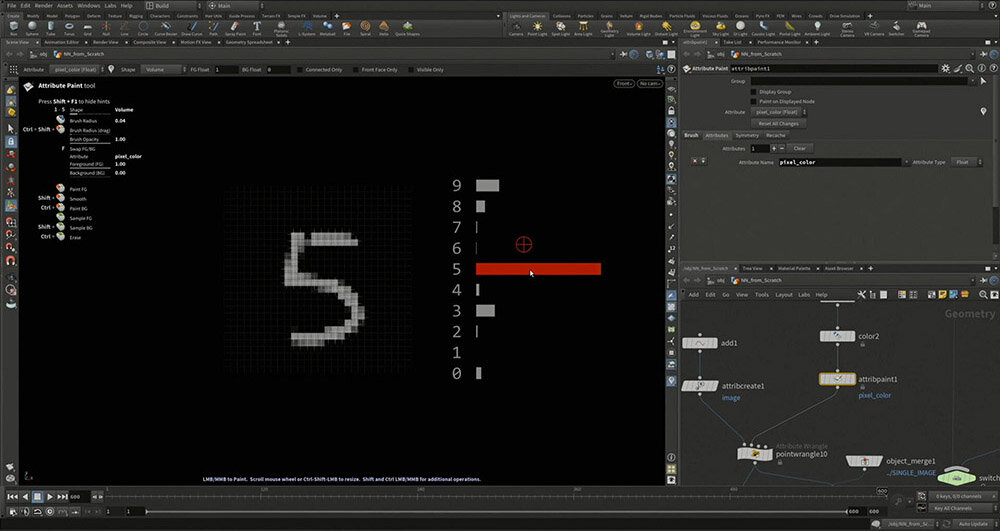
手書きの数字を認識するために、MNISTという画像データセットが用意されている。MNISTの各画像は28×28ピクセルのグレースケールで、訓練用画像60,000枚とテスト用画像10,000枚が含まれている。

さつき先生が今回用意した簡易モデルでは、極端に位置をずらさなければ、手書きの数字をほぼ正しく認識できる。

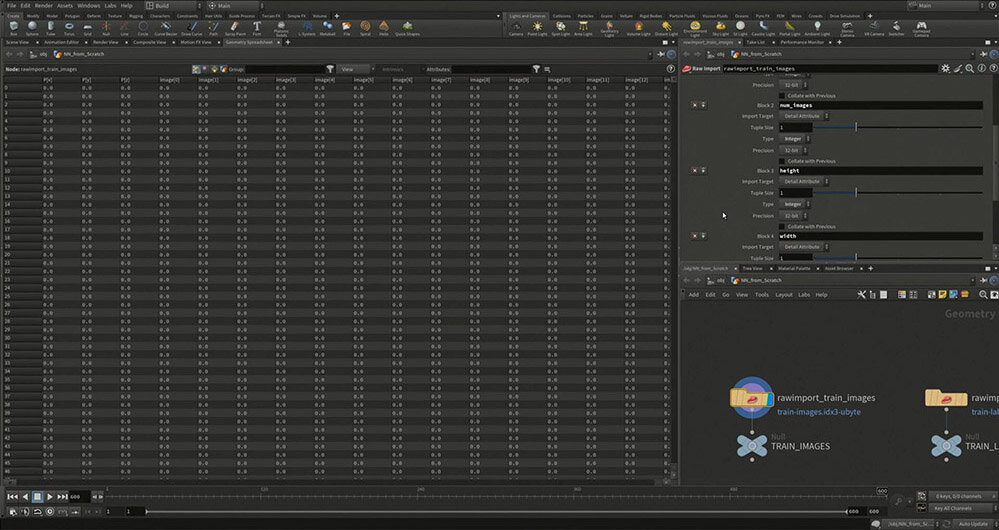
MNISTのデータの中身を見てみると、バイト列のようなデータが格納されている。最初の部分には、データの識別番号やバリデーション用のマジックナンバー、画像の高さなどの情報が含まれている。

ここで、後の処理のために独自にレイヤータイプを指定しておく。"input"は何もしないレイヤー、”affine”、"relu"は後工程の計算方法に則した命名だ。

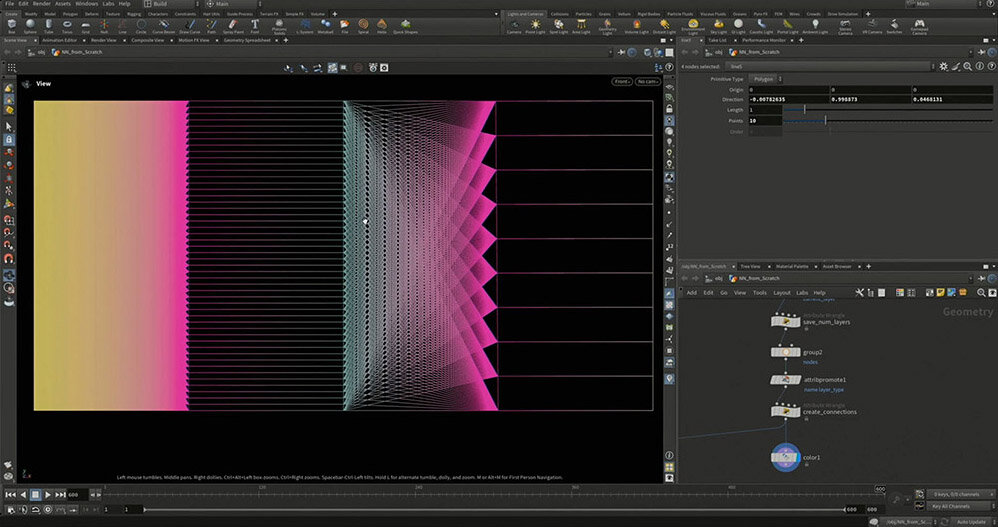
実際に作成したネットワークにインプットを入れると、下図のような結果になる（ここでは、わかりやすいように色を付けている）。

このネットワークでは、784個のインプットをいったん50個に圧縮し、その50個をさらに10個に変換してアウトプットを得ている。この変換の過程で、大量のパラメータが調整されており、その数は何万個にもおよぶ。

これだけのパラメータを手作業で調整するのは現実的ではなく、機械学習による最適化が不可欠となる。

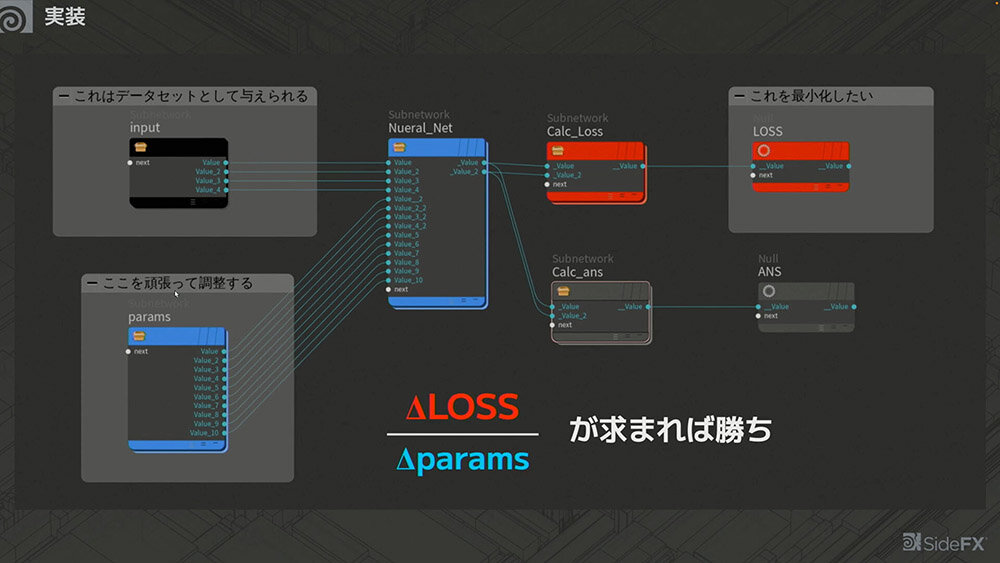
このプロセスを自動化するために、まず計算の方向を事前に決めておく。後ろから計算するのか、それとも前から計算するのかを明確にし、画像を1枚ずつ読み込んで、インプットとしてネットワークに入力。

その時点でのパラメータを使ってネットワーク全体の計算を行い、損失関数の出力値を計算したら、後ろから順にたどりながらパラメータを調整する。この流れをくり返すことで、ネットワークが少しずつ学習していく。

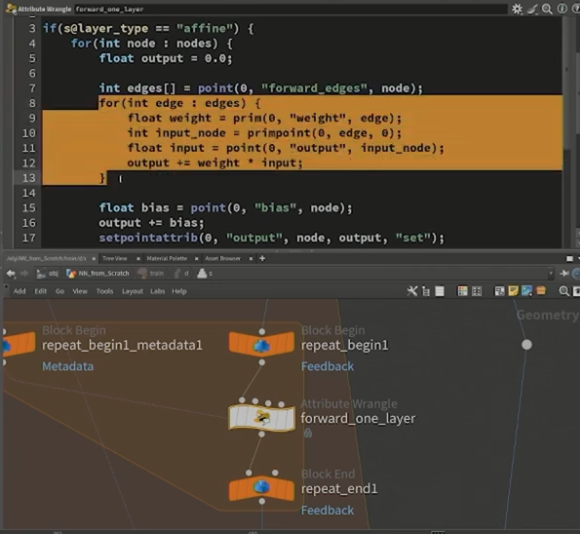
この流れをHoudini上で実装すると、以下のようになる。

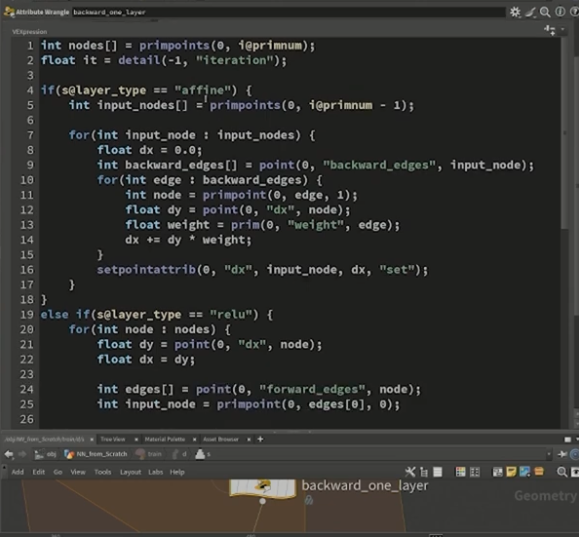
まず、インプットをセットし、［forward_one_layer］と名付けたAttribute Wrangleノード内に、インプットと現在のパラメータを基に次の計算を行う処理を記述する。

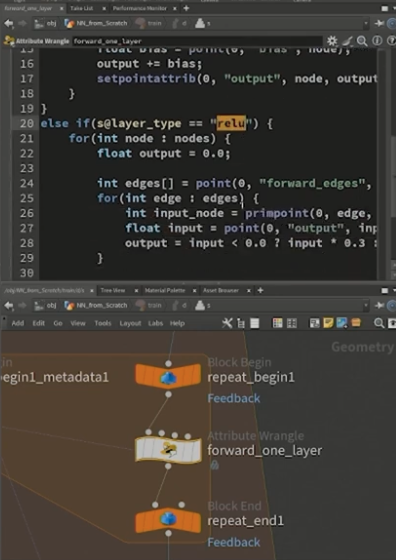
先ほど設定したレイヤータイプがreluの場合は0とのMAXを取り、レイヤータイプがaffineの場合は、各アウトプットを計算するために全てのインプットを参照し、乗算と足し込みの操作を順番に実行する。

• 

• 

続いて、そこで計算したLOSS（損失関数）の値を基に、［backward_one_layer］と名付けたAttribute Wrangleノードで、先述した誤差逆伝播法の作業を行う。

学習の過程では、ウェイトを少しずつ更新するために float lr = 0.001 （lr＝learning rate）という変数を加え、徐々にパラメータをアップデートする。これにより、LOSSの値がトレーニング開始時の 2.3 から最終的に600フレーム後に 0.288 まで低下した。

こうして、バイアスやウェイトが毎フレームごとに調整され、より精度の高い認識が可能になる。最後に、結果を見やすく整理することで、手書きの数字をより正確に自動認識できるようになる。

セッションの最後には、さつき先生の著書『SideFX公式 さつき先生と学ぶ はじめてのHoudini』が紹介された。本書には、「つくりたい！」と思わせるような魅力的な作例が多数掲載されており、1,200枚以上の図解が収録されている。

また、成功の道筋だけでなく、あえて失敗の手順も公開されているのが特徴で、原因と結果を理解しながら学べる内容になっている。Houdiniを学びたい方にとって、貴重な一冊といえるだろう。

講演動画

なお、本講演のスライド資料とHoudiniのデータは以下で配布されている。

つくってまなぶ 機械学習きほんの「き」 - Google ドライブ