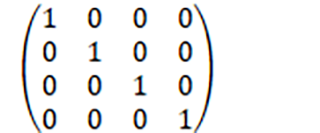クリーク・アンド・リバー社の社内CGスタジオであり、ゲームの3DCGグラフィックス制作を中心に手がけているCOYOTE 3DCG STUDIO。本連載では、同社のTAチームによる制作に役立つ技術TIPSを紹介していく。
TEXT_山本智人 / Tomohito Yamamoto(COYOTE 3DCG STUDIO)
EDIT_三村ゆにこ / Uniko Mimura(@UNIKO_LITTLE)
はじめに
おはこんばんちわ、COYOTE 3DCG STUDIOテクニカルアーティストの山本です。
前回までは、当スタジオの中林から4回にわたり、PhotoshopにおけるテクニカルサポートTipsについて紹介しました。今回はまた、キャラクターの「アニメーション・リギング制御」の話題に戻り、Matrixに関して取り上げてみたいと思います。
「Matrix」と聞くと、扱いに慣れていなければ「何やら得体の知れない概念」に聞こえるかと思います。 Matrixを使用することによって一体何ができるのか、いまいちイメージが湧かないのではないでしょうか。
そこで、今回から3回にわたってMatrixを使った事例を紹介し、初回では「Matrixの初歩」に関して理解を深めてみようと思います。
Step 01:Matrixとは「Transform成分を1つにしたもの」
単刀直入にMatrixについて説明すると、いわゆる数学でいう「行列」で、空間上のトランスフォーム成分、すなわち「移動」、「回転」、「スケール」、「シア」をまとめて取り扱うことができる概念です。
ある地点Aのベクトルとマトリクスをかけ算したり、あるいはある移動成分をもったマトリクスと計算することで、その座標を変換することができます。というのが一般的な説明かと思うのですが、これではなかなかイメージが湧かないと思います。図を使ってイメージを固めながら理解を進めてみましょう。
ある地点にAさんがいるとします。
Aさんは当然「移動」、「回転」、「スケール」、「シア」を保持した状態でその空間上に存在しているわけですが......
この「移動」、「回転」、「スケール」、「シア」をひとまとめにして取り扱うのが「Matrix」になります。
例えば、
Transform = (0.0,0.0,0.0)
Rotate = (0.0,0.0,0.0)
Scale = (1.0,1.0,1.0)
Shear = (0.0,0.0,0.0)
......のMatrixを表すと、
こんな感じの行列です。ちなみに、このような「移動も回転もしていない行列」のことを数学では「単位行列」と呼びます。
この数字の羅列を見て「移動」、「回転」はまったくピンと来ませんよね。複数のトランスフォーム成分をまぜこぜにしているわけですから、そりゃそうです。 不慣れな人に読めるわけがないので、そういうものだと思っていただいて問題ありません。
とりあえずここまでは、「Matrix」とは「トランスフォーム成分をひとまとめにしたかたちである」と理解ができれば十分です!
Step 02:ローカル空間? 親空間? グローバル空間?
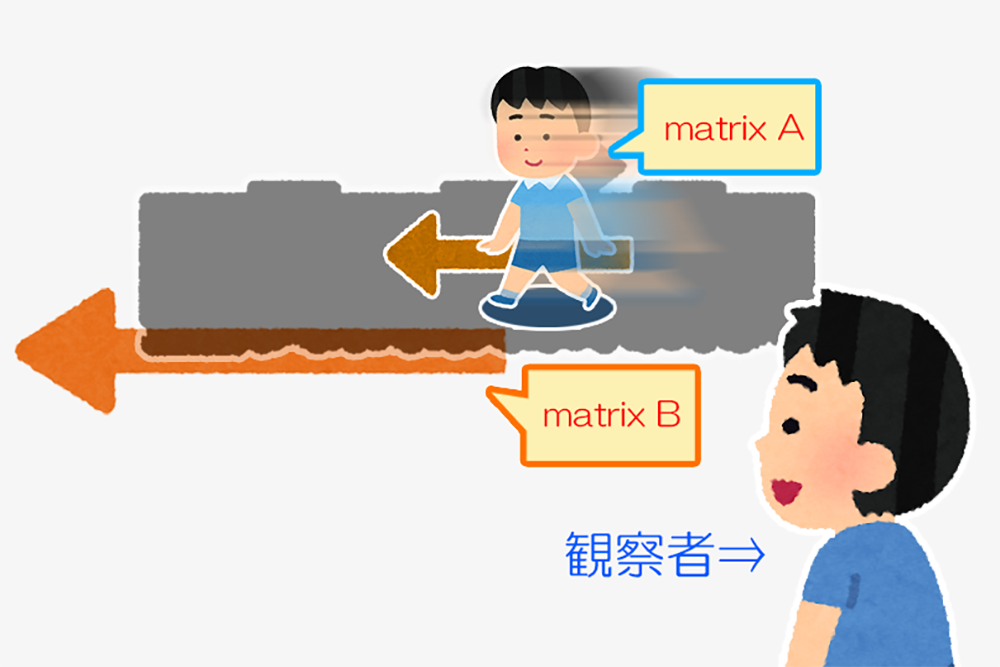
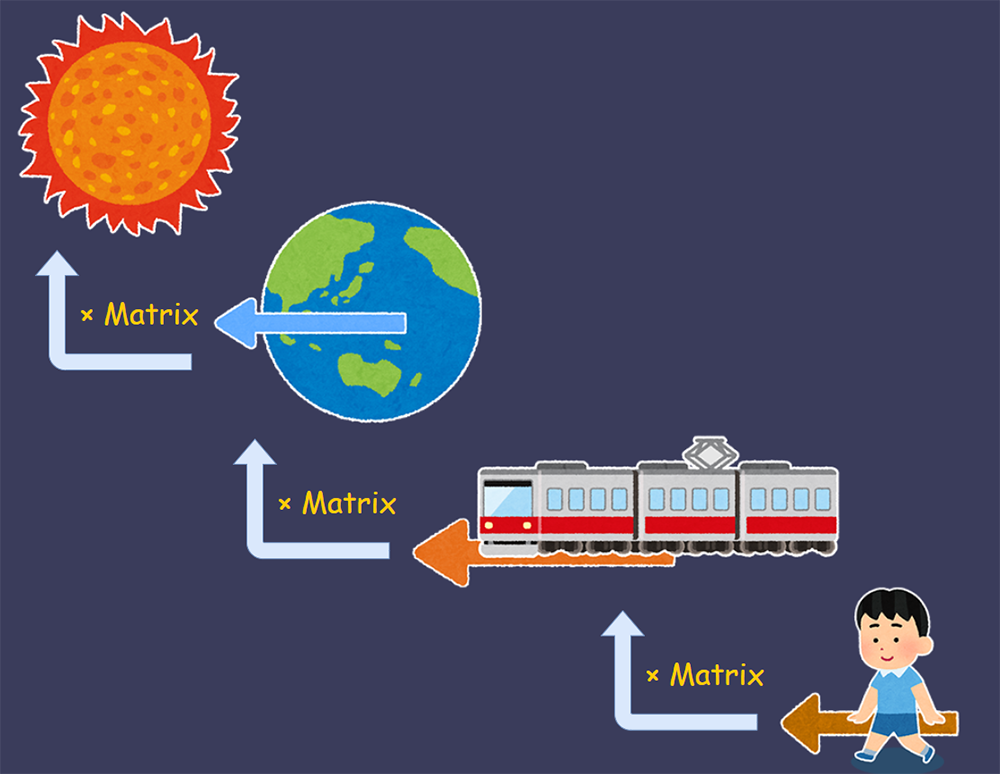
Matrixが何たるかをざっくりと理解したところで、その用途について考えてみましょう。例えば、先ほどのAさんがある地点を歩いていたとしましょう。
この時点で、Aさんは移動成分「A」のマトリクスを保持しているわけですね。では、このAさんは実は電車に乗っていて、その電車は移動成分「B」のマトリクスで移動していたとしましょう。
こう考えてみると、例えばAさんの移動速度は、電車の中から考えると「移動成分A」の移動速度で運動してることになりますが、しかし電車の外からだとどうでしょうか?
Aさんの移動成分「A」に対し、電車の移動成分「B」が加算されますね。もっと言うと、この電車は自転している地球にいるわけで......
さらに、地球は太陽の周囲を公転してるわけで......
はたしてAさんの移動速度はどのように評価すべきなのでしょうか。
ここで考えるべきは、「ローカル空間」、「グローバル空間」という考え方です。電車の中でAさんの移動成分を評価する場合、Aさんと同じ「空間」内での評価になり、これ「ローカル空間」での評価と呼ぶことができると思います。
一方で、電車の外、あるいは宇宙空間でAさんの移動成分を評価する場合、
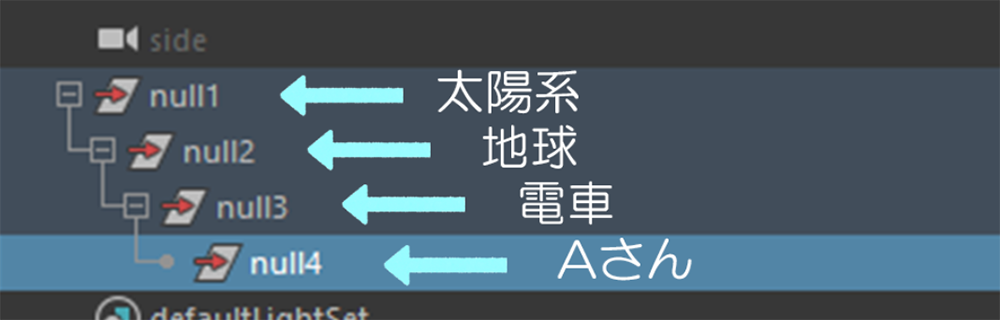
つまり「Maya」に例えて考えると、階層構造になったノードの親にさかのぼって評価する場合、「親空間」での評価と呼ぶことができます。さらに、さかのぼれるだけ親をさかのぼった空間で評価するとき、これを「グローバル空間」での評価と呼ぶことができます。
今回の例では「電車」、「地球」、「太陽系」がそれぞれMayaでいう「親空間」にあたりますが、Aさんの移動成分をそれぞれの空間でどのようにして評価・計算するのでしょうか。
こんなとき、Matrixを使うことで簡単に計算することができるのです。
Step 03:Matrixはかけ算で階層評価ができる
先ほどの「太陽の周囲を公転」しながら「自転している地球の上の電車」に「乗って歩いている」Aさんの移動成分を計算してみましょう。
Matrixはかけ算で階層評価ができます。
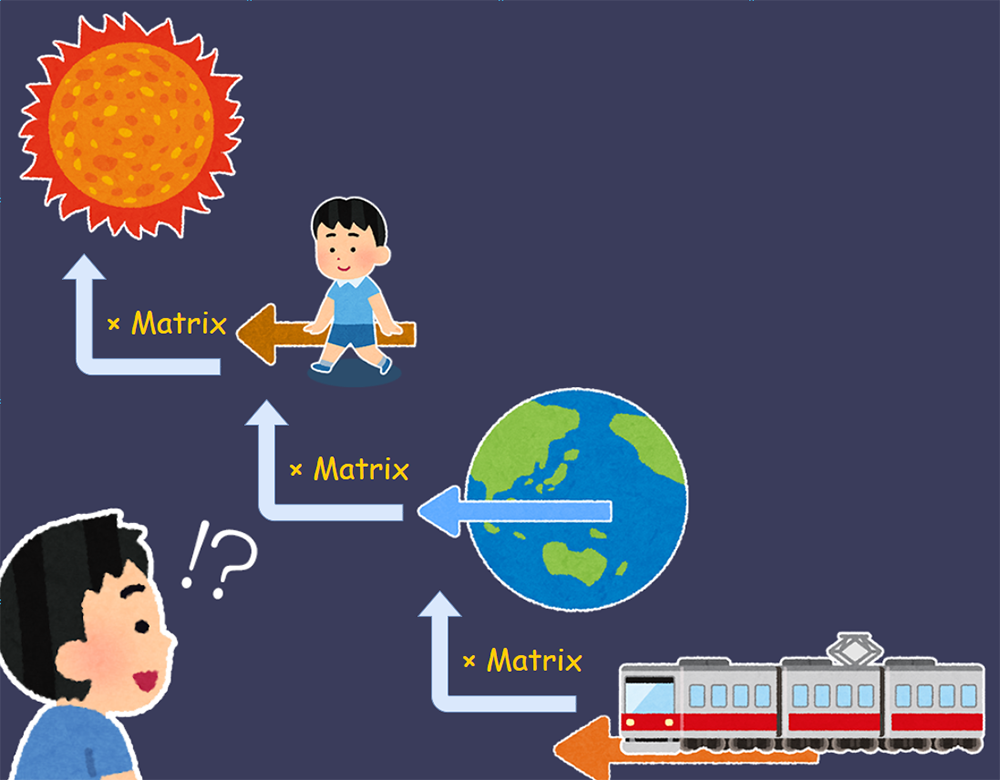
上記の図のように、まず主人公(=Aさん)のMatrixに順番に親空間のMatrixをかけていきます。
AさんのMatrix × 電車のMatrix × 地球の自転Matrix × 太陽の周囲を公転するMatrix
= AさんのグローバルMatrix
......という感じで、Aさんの宇宙空間からみた移動成分の評価を計算することができます。「かけ算をすると、子階層に入れる」みたいな感覚ですね。このようにMatrixはかけ算で親空間を追加していけるのだから、その逆数をかけることで「親空間の打ち消し」もできます。
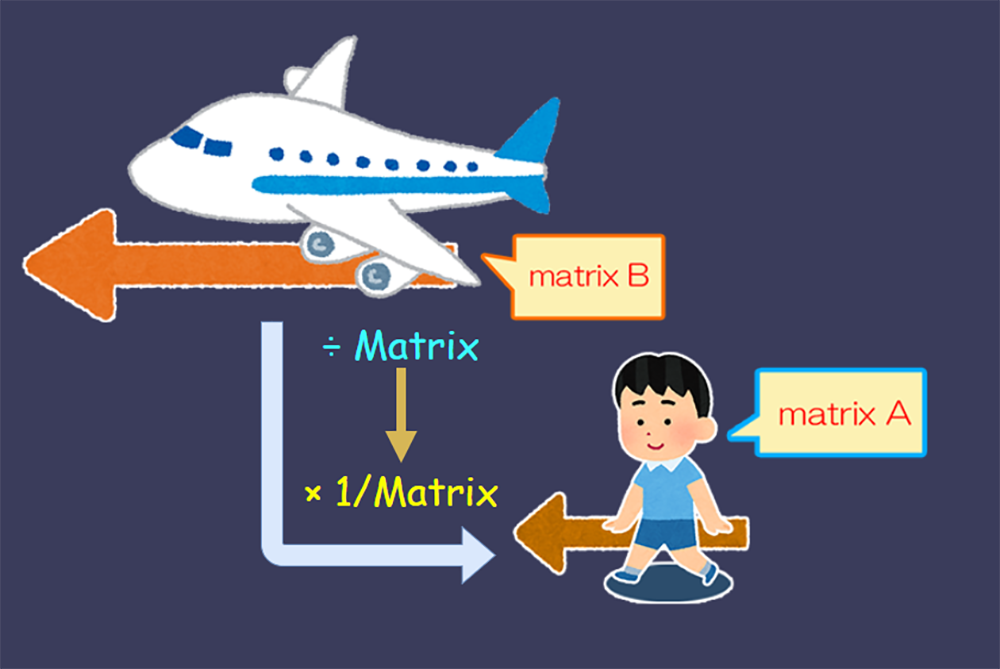
例えば、Aさんが何だかよくわからないけど、猛スピード(移動成分A)で進んでいたとしましょう。
実はAさんは、移動成分Bをもった飛行機の中を走っていたとしたとき、
このときのAさんのローカル空間でのMatrix、すなわちローカルMatrixはいくつになるのでしょうか。
先ほどの例では、Aさんに「親空間を追加」する計算を行いましたが、今回は「親空間を打ち消す」計算を行います。
つまり、上記のように飛行機のMatrixBの逆数(=Inverse Matrix)をAさんのMatrixAにかければ良いのです。つまり「割り算をすると、親子階層を解除する」みたいな感覚ですね。
ここまで書いてふと思うのは、何だかまるでMayaでいうところの「Outliner」上でノードの親子関係を操作している感覚に近いように感じます。
実はその通りで、「Matrixのかけ算」と聞くと何だか小難しい印象を受けがちですが、実態は単に親ノードの関係を切り替えているだけなのですね。単にそれを「Outliner」で行うか「計算やNodeEditorによるリギング」で行うか、のちがいなだけなのでした。
ただ、実際にOutlinerで手作業で操作するオペレーションとは異なり、計算やNodeEditorで親空間の切り替えを行うことができると、必要に応じてリグやモーション制御の中で動的に親空間を切り替えることができるようになります。より複雑なリグの制御や、トリッキーなアニメーション作業に使える「小技」になりえるわけです。
次ページ:
Step 04:Matrixのかけ算には順序がある
Step 04:Matrixのかけ算には順序がある
ここで、Matrixの計算で注意すべき点として「計算の順序がある」ということです。
例えば......
1.0 + 2.0 = 3.0
2.0 × 3.0 = 6.0
4.0 ÷ 5.0 = 0.8
上記の計算は計算順序を変えても結果は変わりませんが、
AさんのMatrixを計算した際に使用した上記の図では、Matrixの計算順序が変わると、結果は大きく異なってしまうため、必ず「子→親」の方向にかけ算をしていかねばなりません。
同様に、逆に親空間を打ち消す場合は「親→子」の方向にかけ算しなくてはなりません。 なれないと混乱するかもしれません。 しかし少し考えてみると当然なんですよね。なぜなら、Outlinerでの親子付け操作をイメージしてみてください。
親子付けの順番を変えてしまうと結果は大きく異なりますね。 理屈はこれとまったく同じです。
「Matrixの計算順序に決まりがある」と言われてしまうと、小難しい印象が先だってなかなか覚えられそうにないかもしれませんが、「Outliner上の操作と同じ」と考えるとどうでしょう。単純にOutliner上でのノード操作による親子関係の操作オペレーションだったら、そこまで間違うことはないのではないでしょうか。
要は「物の見方・捉え方」なんですね。
Step 05:でも本当に? 実験してみよう
ここまで理屈を説明してきましたが、本当にそうなんですかね? 百聞は一見にしかず、実際にMayaで試してみましょう。
1:Matrixのかけ算でペアレント挙動
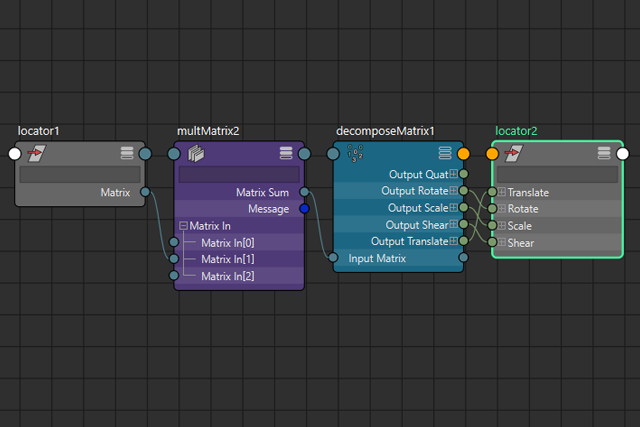
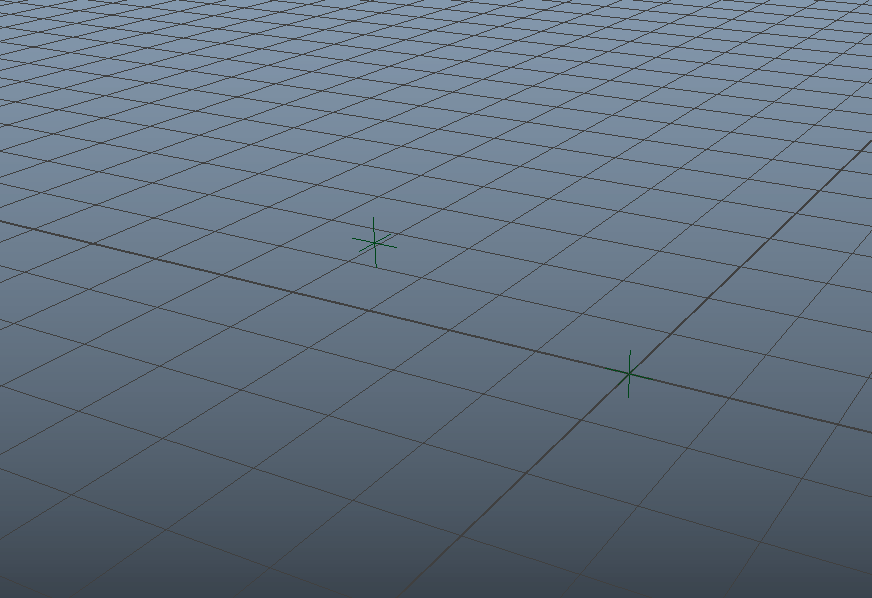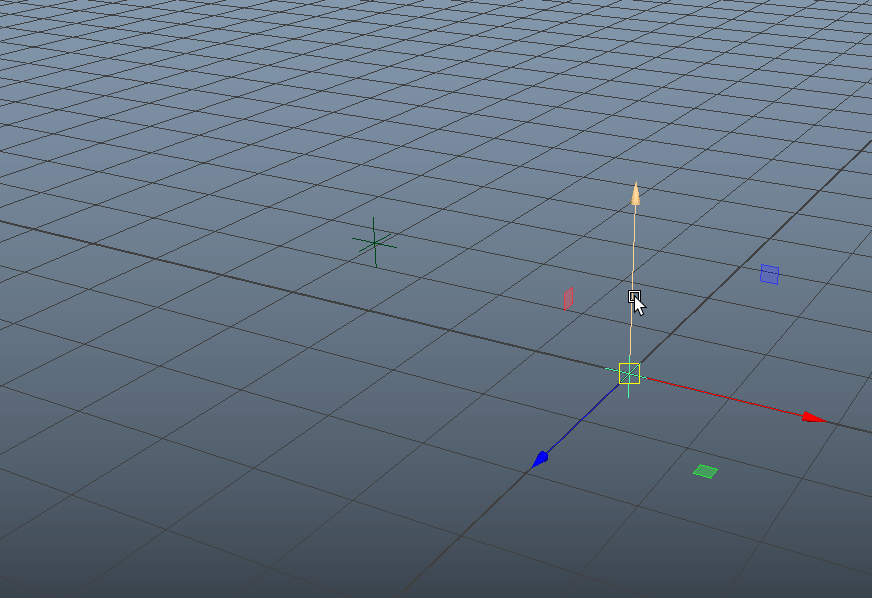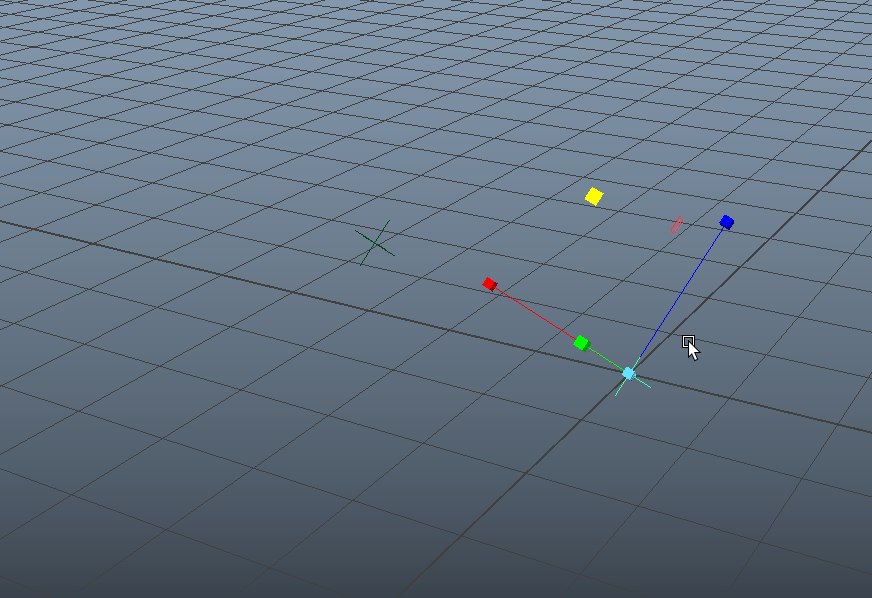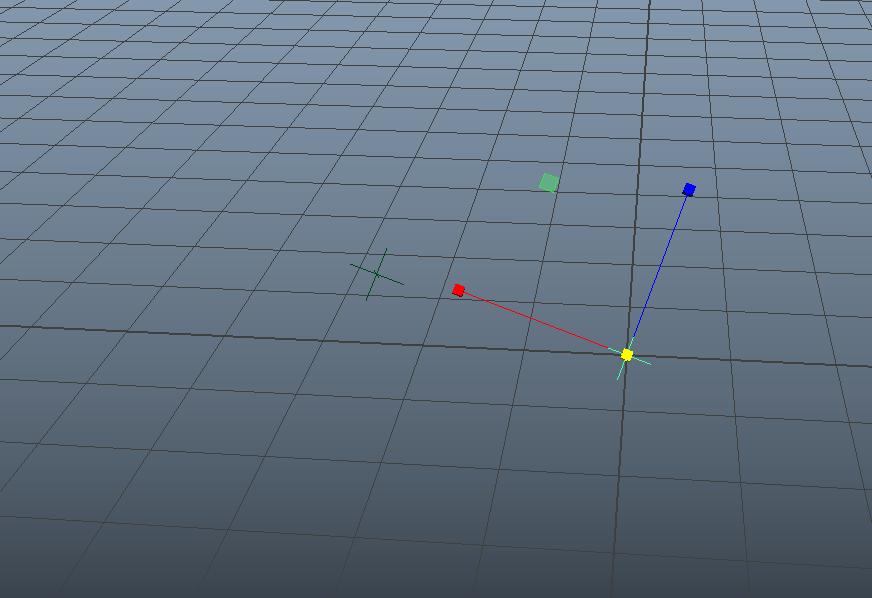
まず「Matrixのかけ算」で仮想的に階層構造に入れていく、すなわち「ペアレント挙動」を実際にやってみましょう。
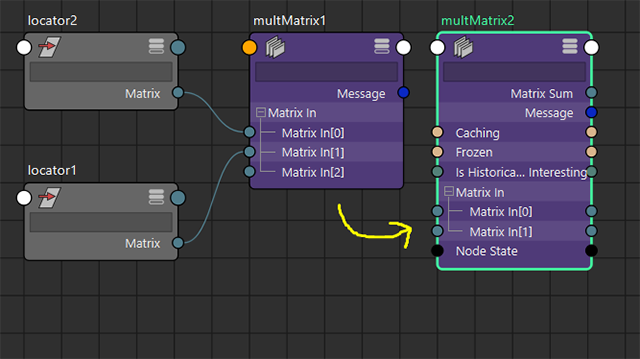
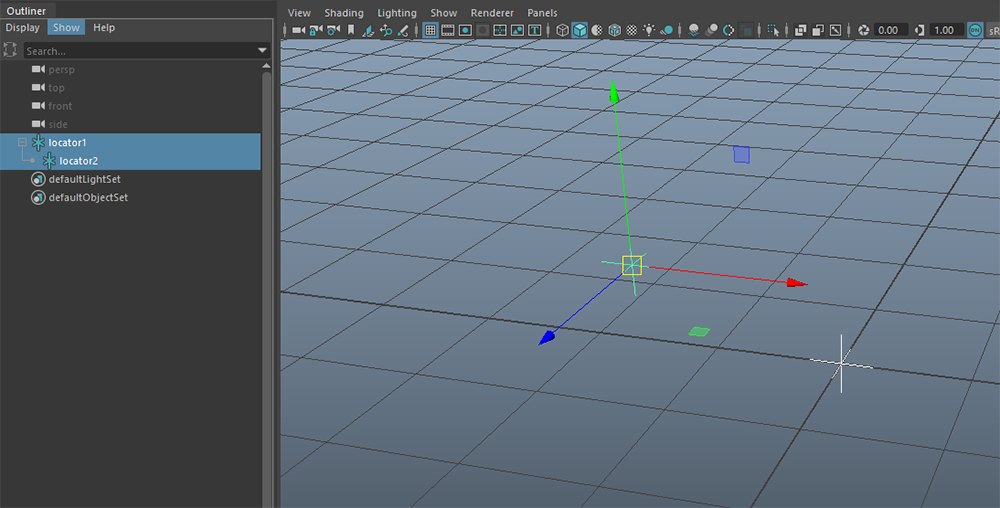
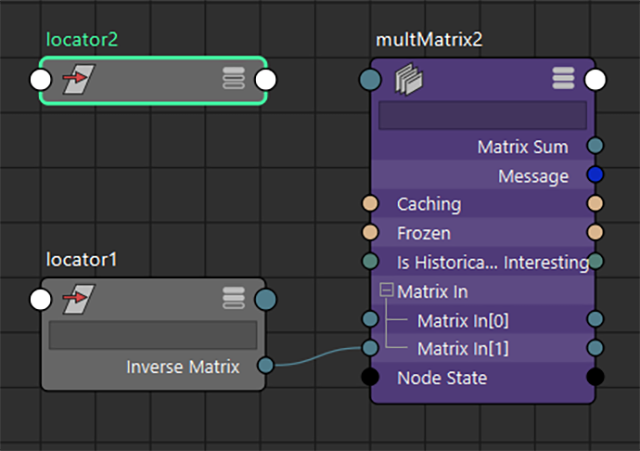
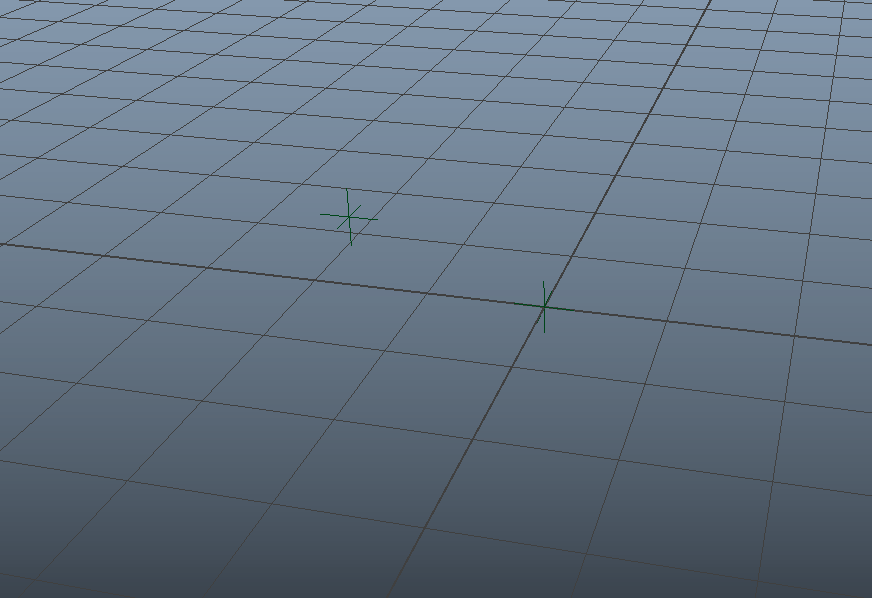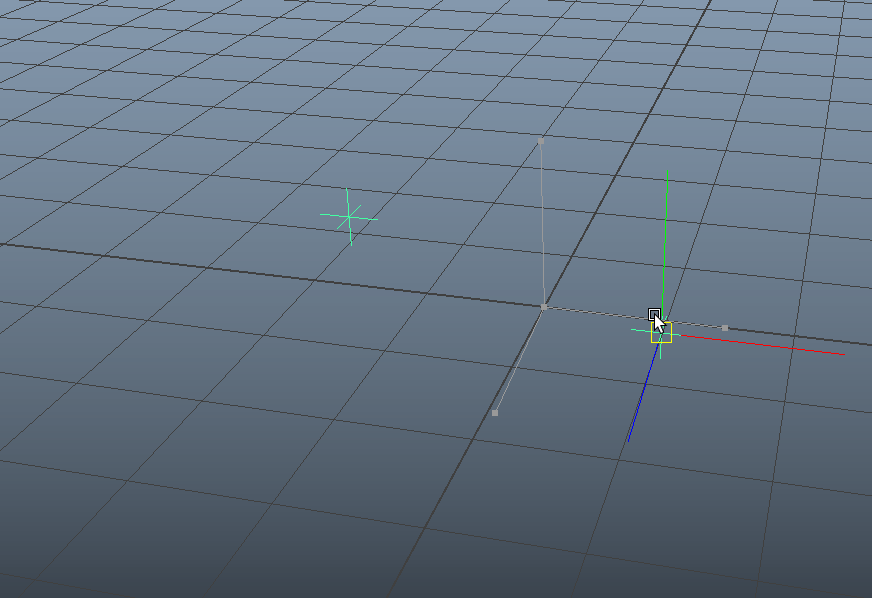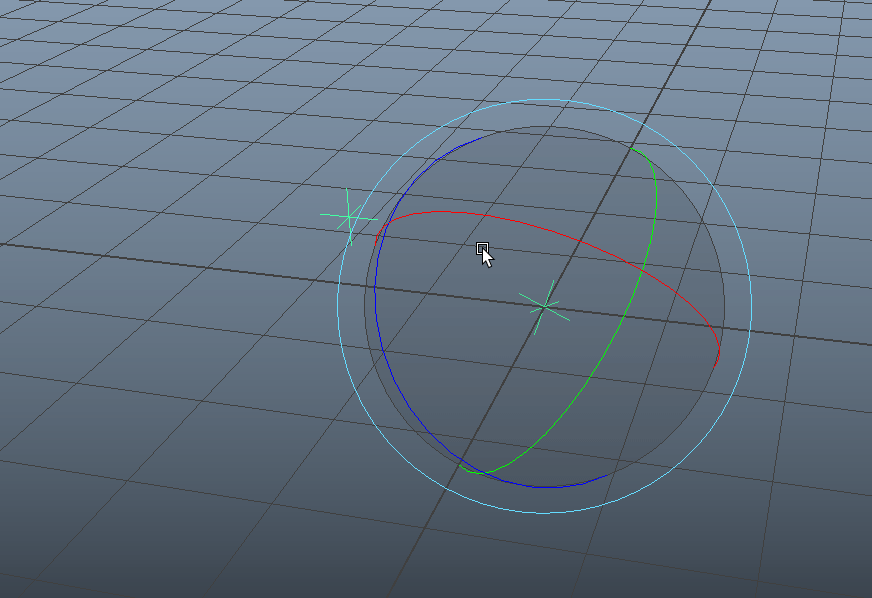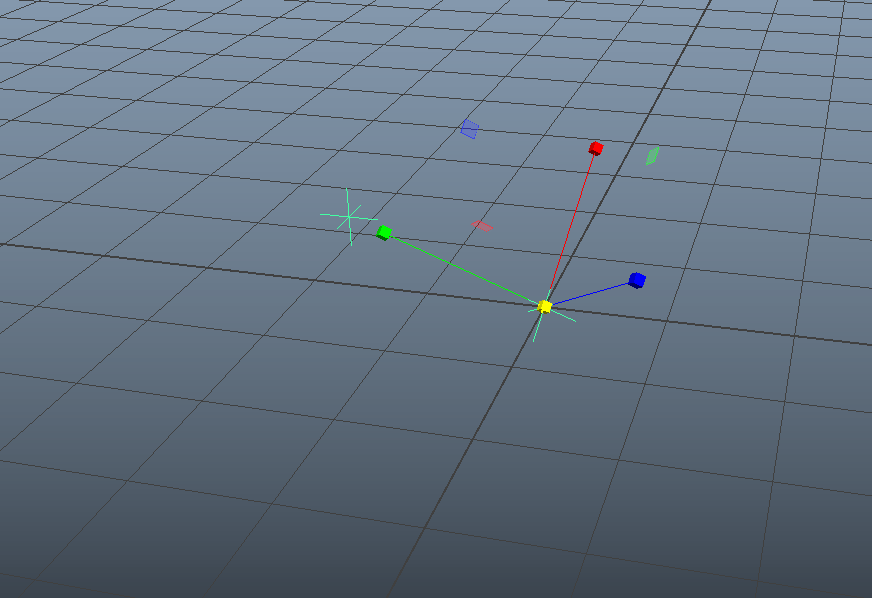
まず、原点位置にロケータ [localor1] を置き、少し離したところにもう1つロケータ [localor2] を配置します。少し離したところのロケータを原点位置のロケータの子階層に入れたような挙動を実現してみたいと思います。
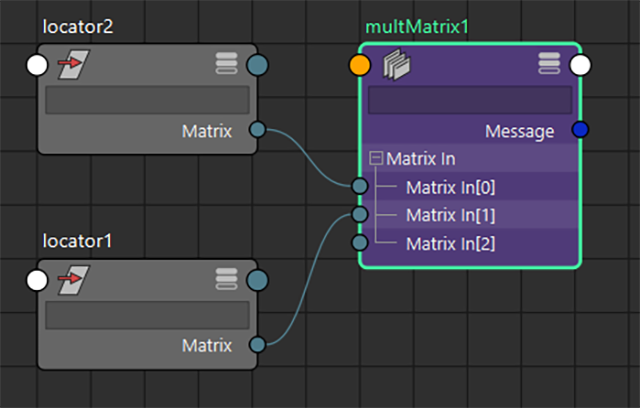
NodeEditorを出し、まず「multMatrix」ノードを作成します。
[locator2]のMatrixアトリビュートをmultMatrixノードの [Matrix In[0]] に接続し、[locator1]のMatrixを [Matrix In[1]] に接続します。ここで、ちょっと小技を使います。
アトリビュートを接続したmultMatrixノードをいったん複製し、古い方は削除します。
こうすることで、今接続したMatrixの値を [Matrix In[0]] に残した状態で接続を解除することができます。通常では「setAttr」コマンドなどを使って、スクリプトから値を設定しないとオフセットの値として設定できないのですが、このオペレーションだと少しだけ楽ができます。(;^_^A
※Maya 2022までで同様の操作が可能であることは確認済み
ここで残したMatrixの値は、[locator2]が保持しているオフセット値として残したいので、このようにノードに情報を残しました。
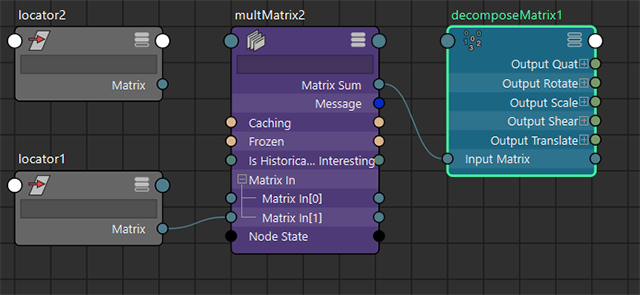
改めて [locator1] のMatrixを [Matrix In[1]] に接続し、[locator2] のOffset Matrixと [locator1] のMatrixのかけ算を計算させるようにします。
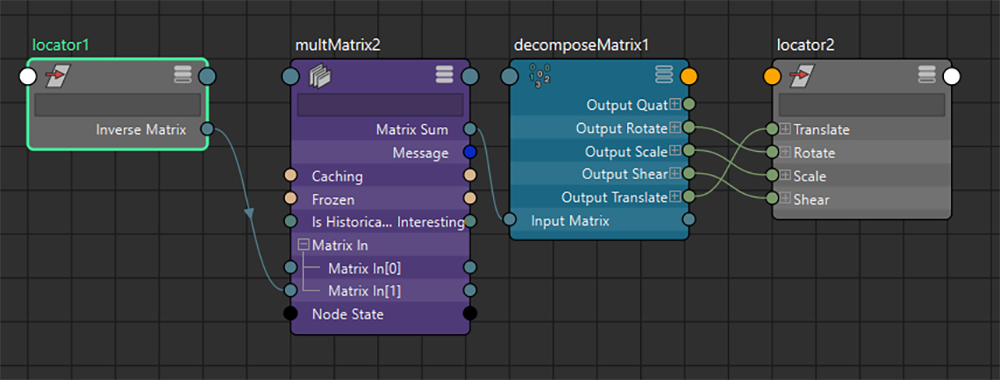
次に「decomposeMatrix」ノードを作成して、multMatrixノードの計算結果と接続させます。decomposeMatrixノードはMatrixから「移動」、「回転」、「スケール」、「シア」成分などを分解し、抽出するためのノードです。
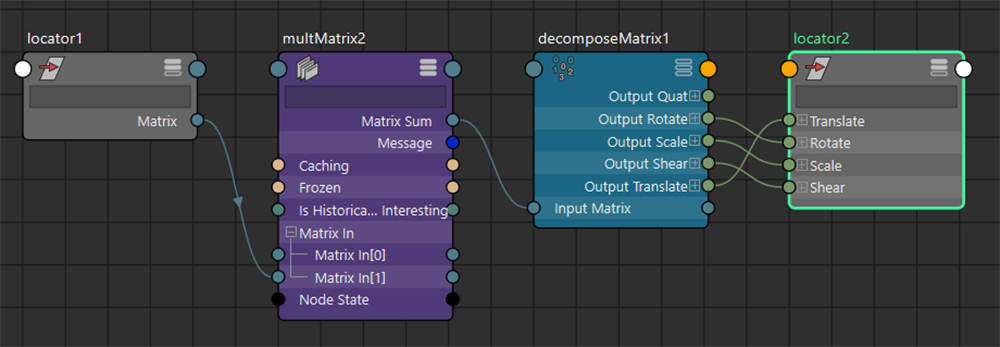
decomposeMatrixノードから [locator2] に対して、「移動」、「回転」、「スケール」、「シア」の成分を接続させます。そして [locator1] を動かすと......
このようにペアレント挙動が実現します。
2:Inverse Matrixのかけ算で階層解除
今度は「階層挙動の打ち消し」を行なってみましょう。
同様にロケータを2つ生成しますが、今度は [locator2] を [locator1] の子階層に入れてみます。
この状態だと(同然のことながら)[locator1] を動かすと、つられて[locator2]は移動・回転します。
ここで、先ほどと同様にNodeEditorから「multMatrix」ノードを作成します。
今度は、Matrixではなく「worldMatrix」のアトリビュートをmultMatrixノードに接続します。worldMatrixアトリビュートはその名の通り、そのノードのグローバルMatrixを返します(内部的には最上位階層までさかのぼって、順に自身のMatrixをかけていった結果を返しています)。
先ほどと同様にオフセットとしてMatrixを残し、今度は [locator1] のMatrixではなく「inverseMatrix」を接続して......
decomposeMatrixと接続して、「移動」、「回転」、「スケール」、「シア」を[locator2]に接続します。
[locator1] を動かすと......
動かない! ハラショー!
3:計算順序を変えてみると......?
では、実際に計算順序を変えてみるとどうでしょうか。最初に行なった「Matrixのかけ算」の例で試してみます。
もともとの接続では、[locator1] のオフセットがMatrix In[0] に来ていましたが、
これをMatrix In[1] に変えて接続を構築してみます。
[locator1] を動かすと......
うーん。全然挙動がちがいます。
このように、計算順序はそのロジックに合わせておかないと、制御が上手くいかないということがわかりました。
Step 06:まとめ
今回は、Matrixに関する初歩的な概念の紹介に留まりましたが、今までMatrixに対して難しい印象を抱かれていた方々が、多少なりともMatrixに対して親しみを感じていただければ幸いです。
電車に乗ったときに「今、電車のMatrixが乗算されたな」とか、あるいは電車を降りたときに「電車のInverseMatrixが乗算されたな」などと、「身のまわりのMatrix」を感じることができるでしょう!
えっ? そんなことはない?......あぁ......そう、ですか。
さて次回からは、今回紹介したMatrixの知識を使って、Matrixの制御をリグやアニメーション作成に応用した例を紹介したいと思います。
では、今回はこのへんで。 サヨナラ! サヨナラ! サヨナラ!!
Profile.
-

-
山本智人/Tomohito Yamamoto(COYOTE 3DCG STUDIO)
ゲーム開発会社にてグラフィックアーティストとして、モデリング・モーション・エフェクト・UIなどオールラウンドのグラフィック制作を経験後、テクニカルアーティストに転身。現在は株式会社クリーク・アンド・リバー社 COYOTE 3DCG STUDIOにて、社内外問わずアーティストのDCCツールサポートや制作パイプラインの提案・作成・運用を行う。特にアニメーション制御やモーション制作周りのテクニカルサポート・リガーとして様々なプロジェクトに従事