クリーク・アンド・リバー社の社内CGスタジオであり、ゲームの3DCGグラフィックス制作を中心に手がけているCOYOTE 3DCG STUDIO。本連載では、同社のTAチームによる制作に役立つ技術TIPSを紹介していく。
TEXT_山本智人 / Tomohito Yamamoto(COYOTE 3DCG STUDIO)
EDIT_三村ゆにこ / Uniko Mimura(CGWORLD)
はじめに
おはこんばんちわ。休日の昼、家族にパスタをつくったけどまったく味がしない謎物体を提供した、COYOTE 3DCG STUDIO テクニカルアーティスト(以下、TA)の山本ほっさんです。
全3回に渡って紹介するテクニカルTIPS「ノードの回転制御」。今回はシリーズの最終回です。
・ベクトルを使ったノードのBend制御(第1回)
・Quaternionを使ったRoll成分の分解(第2回)
・ベクトルの活用(内積・外積・三角関数)←イマココ!
ここまでお話しした中でもいくつか数学的なアプローチを紹介してきましたが、意外と数学にはグラフィカルな一面があったと思います。今回は「ベクトルの活用(内積・外積・三角関数)」と称し、ひとまず簡単なところで、ExpressionでVector型を使ったAim Constraintの再現をなぞりつつ、「数学のグラフィカルな一面」を中心に紹介していきます。
Result:結果を先に
Aim constraintをExpressionで再現するには、以下のような手順を踏みます。
①:対象のノードとAim targetの座標から対象のノード→Aim target の単位ベクトルを求める
②:①で求めたベクトルの回転前後のベクトルから、内積と三角関数を用いて回転角度を計算する
③:①で求めたベクトルの回転前後のベクトルから、外積を用いて回転軸のベクトルを計算する
④:②と③の結果をaxisとangleとして値をExpression外に出し、Quaternion経由でEuler変換
⑤:対象ノードの回転アトリビュートに接続
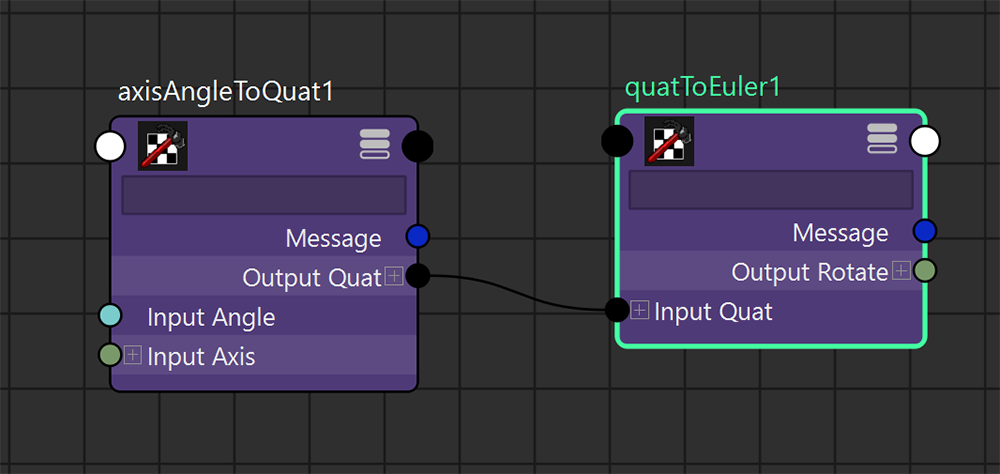
ExpressionのコードとNodeEditorの結果は以下の通り。
vector $Pos_targetNode =
«argetNode.translateX,targetNode.translateY,targetNode.translateZ»;
vector $Pos_aimNode =
«aimVector.translateX,aimVector.translateY,aimVector.translateZ»;
vector $defaultAimVector = <<1.0,0.0,0.0>>;
vector $aimVector = unit($Pos_aimNode -$Pos_targetNode);
//aim rotate
float $dotProd = dot($defaultAimVector,$aimVector);
vector $rotateAxis = cross($defaultAimVector,$aimVector);
float $rotateAngle = acosd($dotProd);
axisAngleToQuat1.inputAxisX = $rotateAxis.x;
axisAngleToQuat1.inputAxisY = $rotateAxis.y;
axisAngleToQuat1.inputAxisZ = $rotateAxis.z;
axisAngleToQuat1.inputAngle = $rotateAngle;
コードとNodeEditor上はわりとシンプルにできますね。
では、1つずつ紐解いてみましょう。
Step 00:そもそも「ベクトル」ってなに?
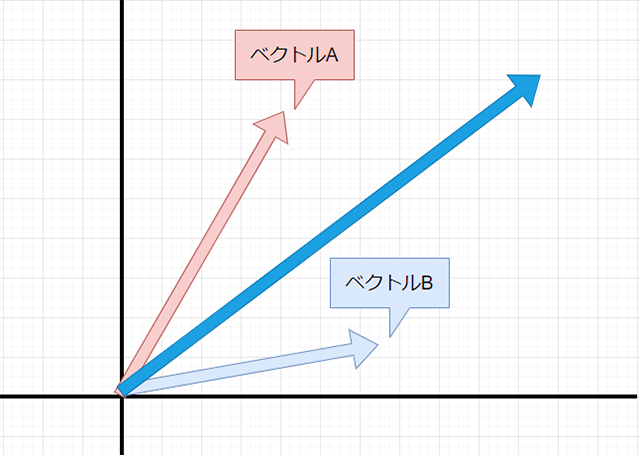
設計と実装を進める前に、まず「ベクトルとは何か」を少し考えてみます。3DCGで扱うベクトルとは主に「空間ベクトル」を指しており、一般的には「向き」と「長さ(大きさ)」をもつ「量」と言われます。文章解説ではいまいちワカランと思いますが、以下の図で見てみるとイメージしやすいのではないでしょうか。
Maya上のTranslateの値にあるように、3D空間上の点は「X」、「Y」、「Z」の3つの値で定義できます。この(X,Y,Z)の値を「座標」としてではなく、原点座標からの「向き」と「距離」として考えるのが「ベクトル」にあたります。
原点座標から「あっち」とか「あそこ」などと指し示すイメージにも近いかもしれませんね。
ベクトルは「足し算・引き算」ができる
そしてこの「向き」と「長さ」をもつ概念ベクトルは、お互いに「足し算・引き算」することができます。数式的に書くと......
( x, y, z ) - ( x', y', z' ) = ( x+x', y+y', z+z' )
と表し、すなわち3つの値を同時に計算できる概念というわけです。
もっと図形的に考えると......
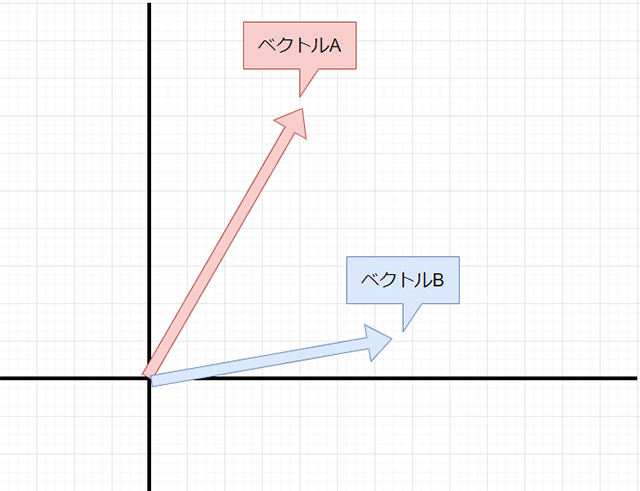
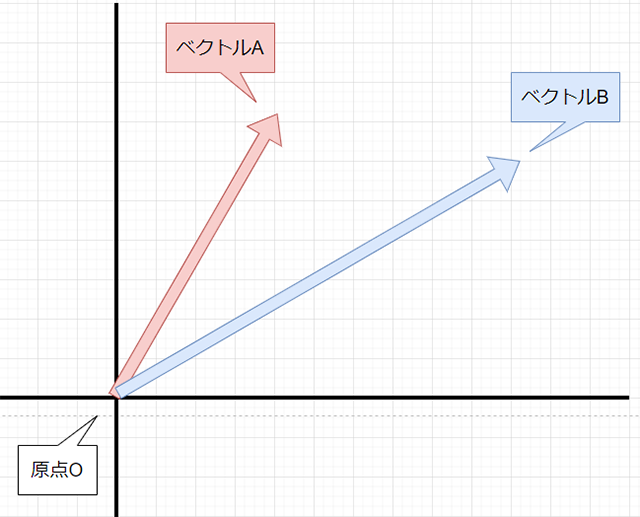
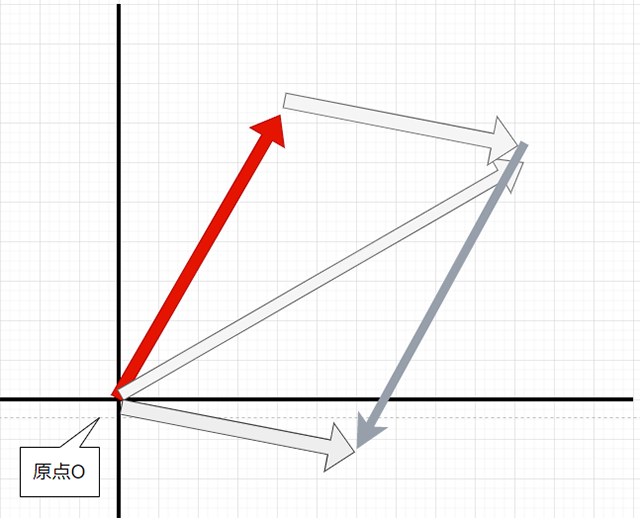
座標平面上にある「ベクトルA」、「ベクトルB」に対しての「足し算」を考えてみます。
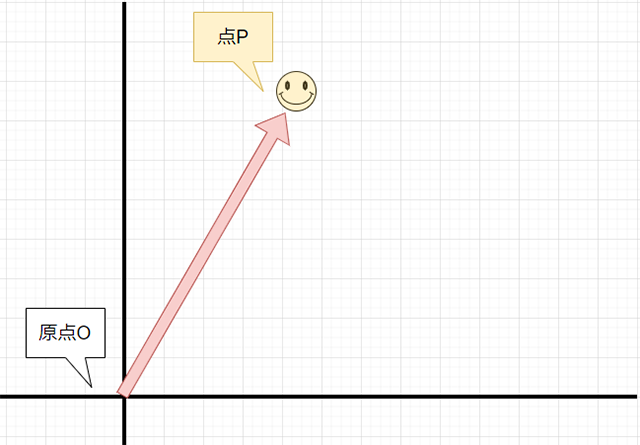
まず「ベクトルA」の分だけ、原点Oから点Pが移動したとします。
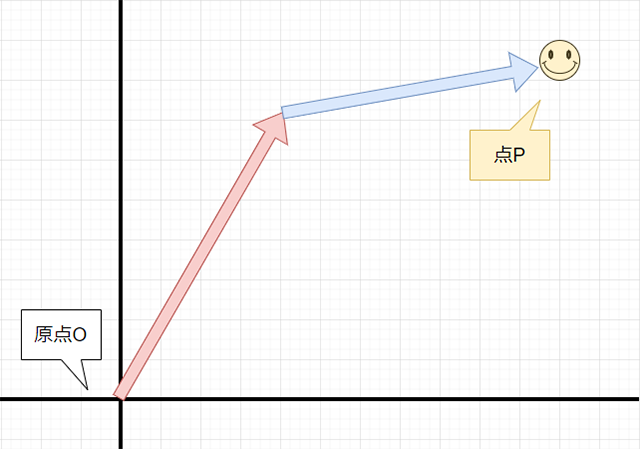
次に、現在の位置から追加で「ベクトルB」の分だけ点Pが移動したとします。
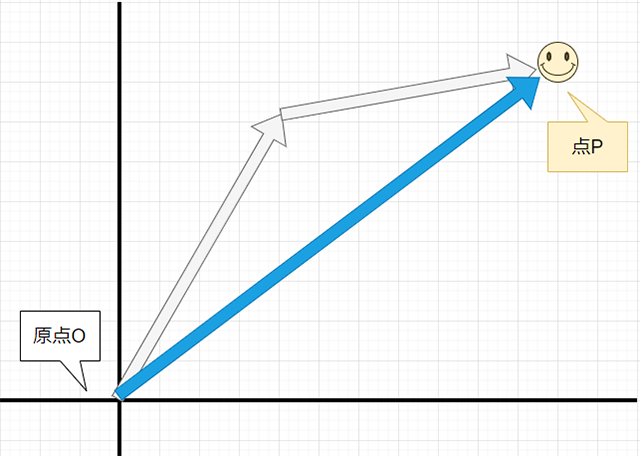
すると、最終的には点Pは原点Oからこのように移動したことになり......
すなわち、「ベクトルA」と「ベクトルB」の足し算は、このように表すことができるわけです。また、物理学の側面からもベクトルの足し算を考えることができます。
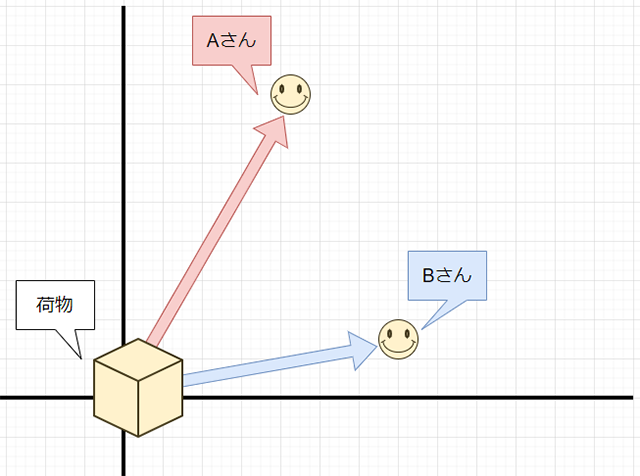
例えば、重たい荷物が原点にあったとして、それをAさん、Bさんがそれぞれ「ベクトルA」、「ベクトルB」分の力で各々引っ張ったとします。
すると、この原点位置にある荷物にかかる力は......
このように平行四辺形の図で考えることができ......
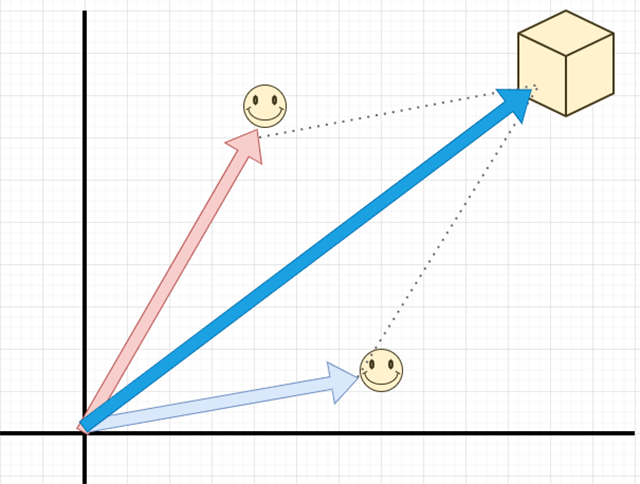
その平行四辺形の対角線に沿って、このような力がかかります。これもまた「ベクトルA」と「ベクトルB」の足し算の結果に等しくなります。ちなみに物理学では、このような2つの力(ベクトル)が合わさった力(ベクトル)を「合力」と呼びます。ベクトルは「数式」というより図形的・幾何学的なロジックですよね。
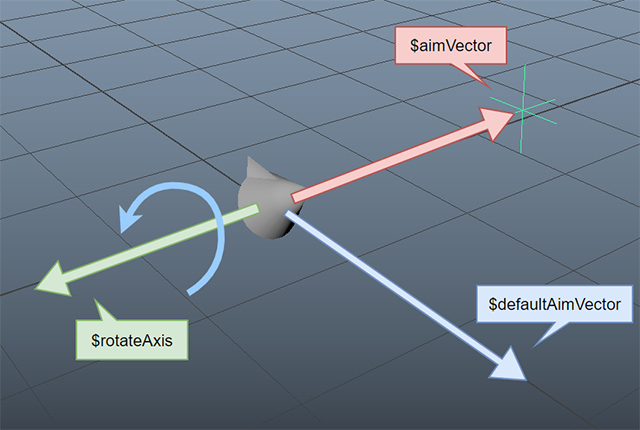
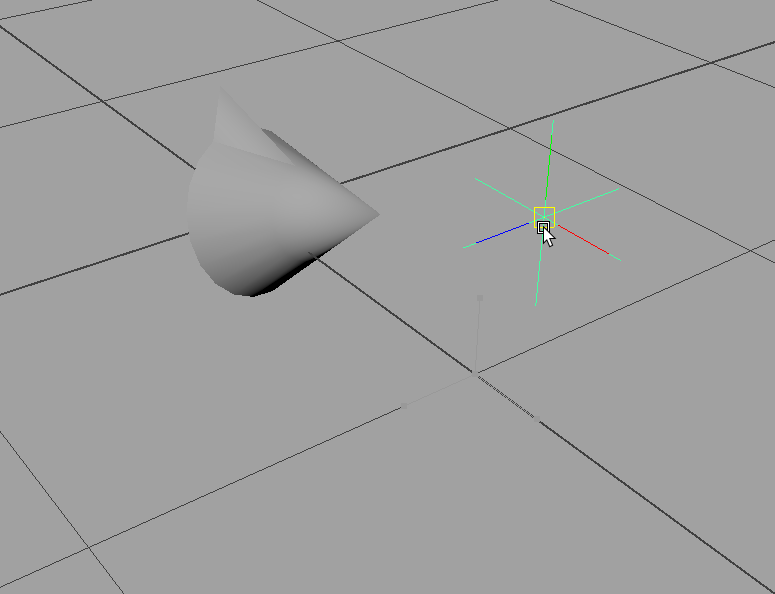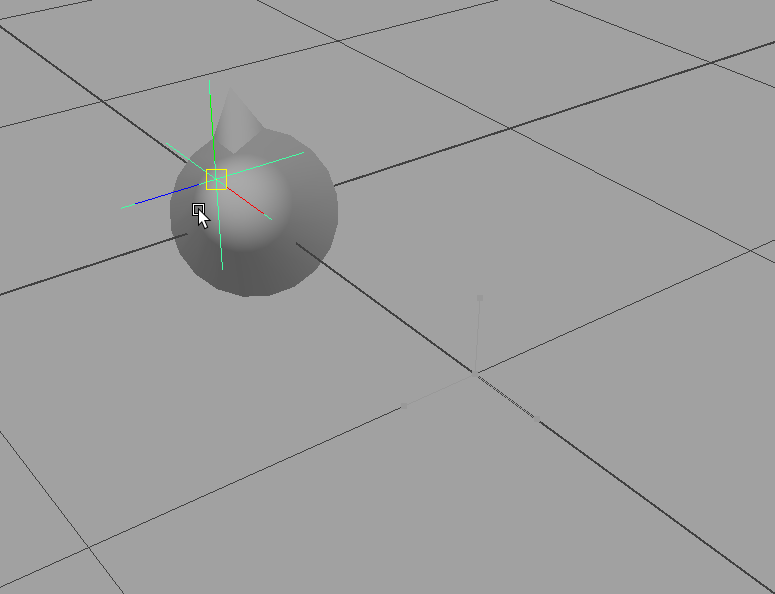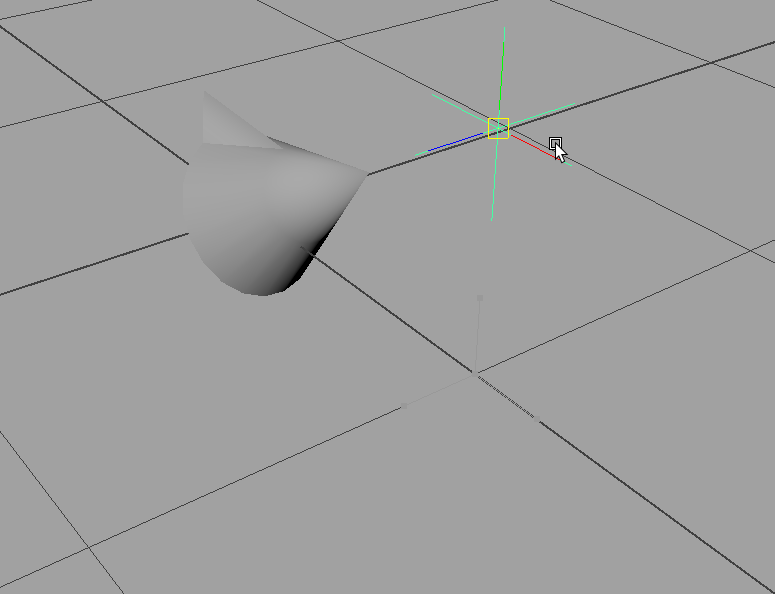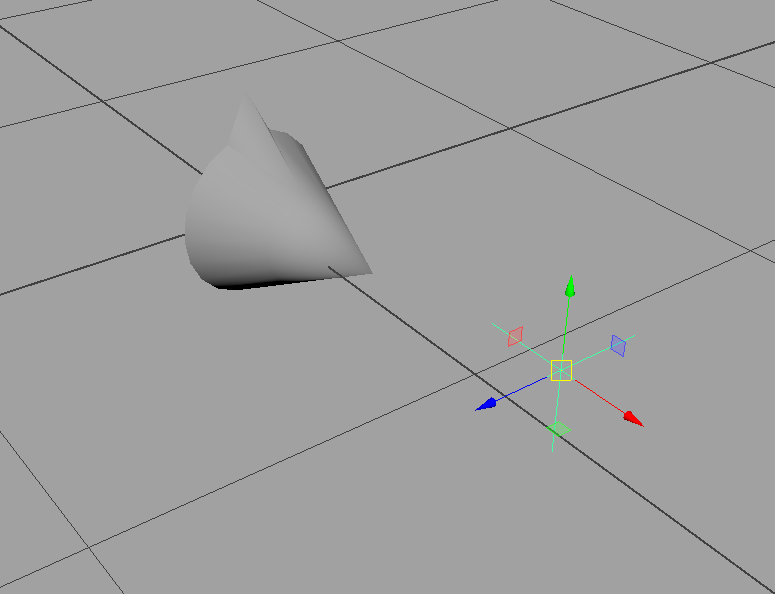
Step 01:対象のノードから見たAim targetへのベクトルは?
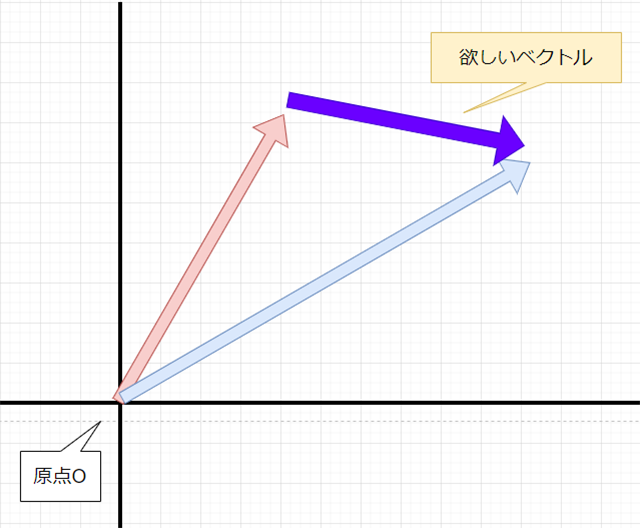
さて、Aim Constraintの話に戻りましょう。上記の例は、空間上の座標(X,Y,Z)を原点位置から見たベクトルとして考えるお話でした。では、任意の座標A(X,Y,Z)から見た、別の座標B(X',Y',Z')へのベクトルはどのように表すのでしょうか。
上記のように座標Aと座標Bの値だけでは、単に原点からのベクトルにしかなりません。対象のノードから見たAim targetへの向きを知りたいので......
欲しいのはこのベクトルです。
このベクトルを原点位置に平行移動させてくると......
こうなります。
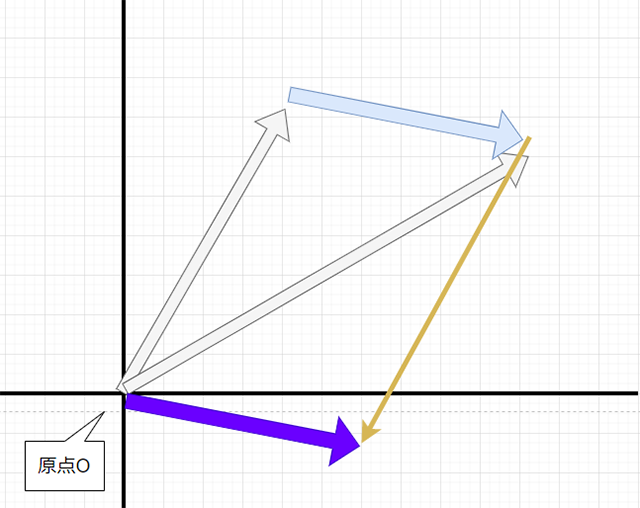
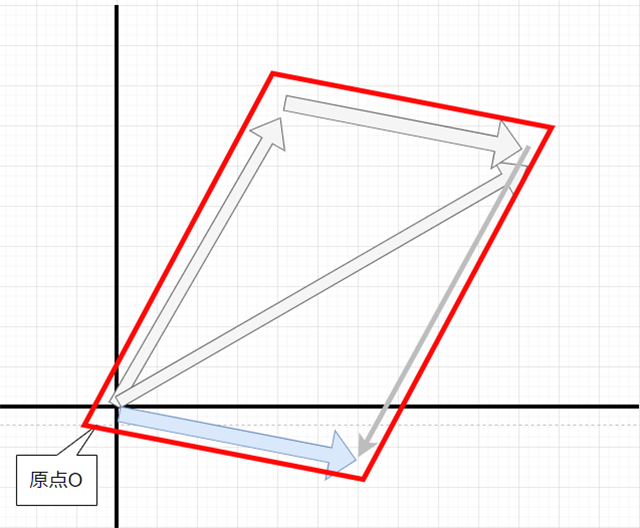
さて、ここで気付くべきは、
この平行四辺形のイメージです。
ここのベクトルは、
ベクトルAの逆ベクトルにあたるので、つまり求めたいベクトルABは......
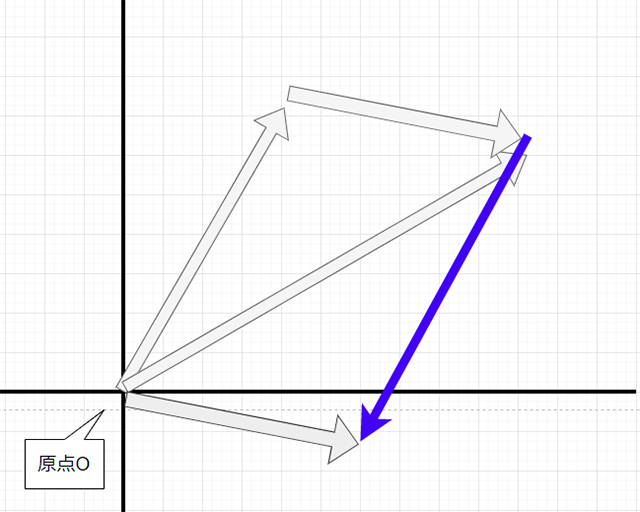
ベクトルB+(ーベクトルA)すなわち、ベクトル「BーベクトルA」と表すことができるわけです。ですので、
TargetNodeからAim target ノードまでのベクトルはExpressionでは......
vector $Pos_targetNode =
«targetNode.translateX,targetNode.translateY,targetNode.translateZ»;
vector $Pos_aimNode =
«aimVector.translateX,aimVector.translateY,aimVector.translateZ»;
vector $aimVector = $Pos_aimNode -$Pos_targetNode;
このように表すことができます。
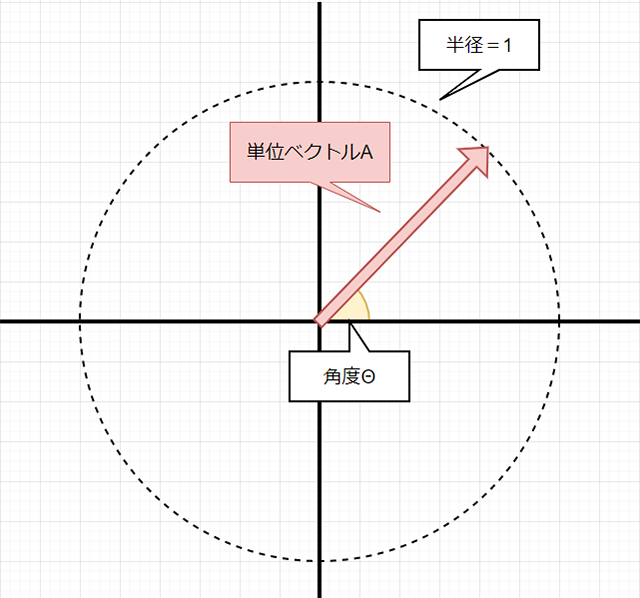
今回はTargetNodeから見たAim targetの「向き」成分のみを知りたいので、上記で取得した$aimVectorを「正規化」して「単位ベクトル」にします。
単位ベクトルとは、長さ1のベクトルのことで......
正規化して単位ベクトルにすると、このように原点Oを中心とした半径1の同心円状に終点があるベクトルとすることができ、純粋に「向き」だけを評価したい場合に便利になります。ちなみに、ベクトルを正規化するには便利なMELコマンドがあり、
vector $aimVector = unit($Pos_aimNode -$Pos_targetNode);
このように、「unit」というコマンドに通すだけで、正規化された「長さ1」の単位ベクトルにすることができます。
次ページ:
Step 02:2つのベクトルの織りなす角度を求める?
Step 02:2つのベクトルの織りなす角度を求める?
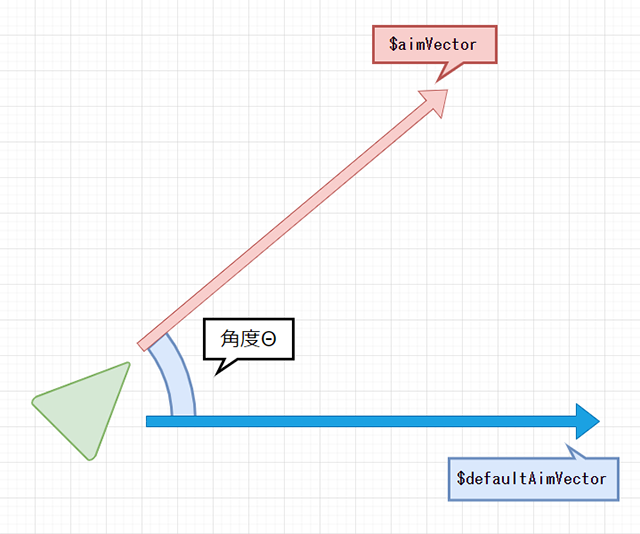
次に、現在の「$aimVector」の向きが初期値よりどの程度変化したかを見て、その回転角度を求めたいと思います。まず、もともとの「$aimVector」の値、すなわち初期値を定義します。
vector $defaultAimVector = <<1.0,0.0,0.0>>;
この初期値の定義は、状況に応じてふさわしい値を設定していくべきですが、ここではX軸方向を正面に向いている状態を初期値として定義しました。さて、この初期値のベクトル「$defaultAimVector」と、現在のベクトル「$aimVector」を比較し......
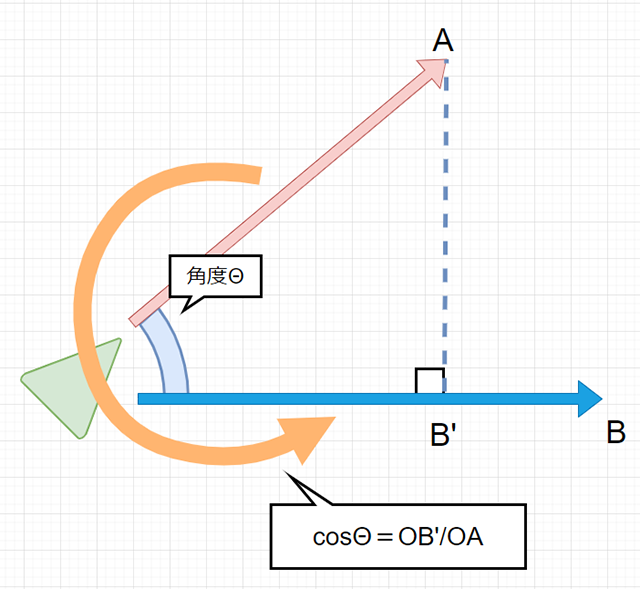
その2つのベクトルの織りなす角度を計算したいと思います。
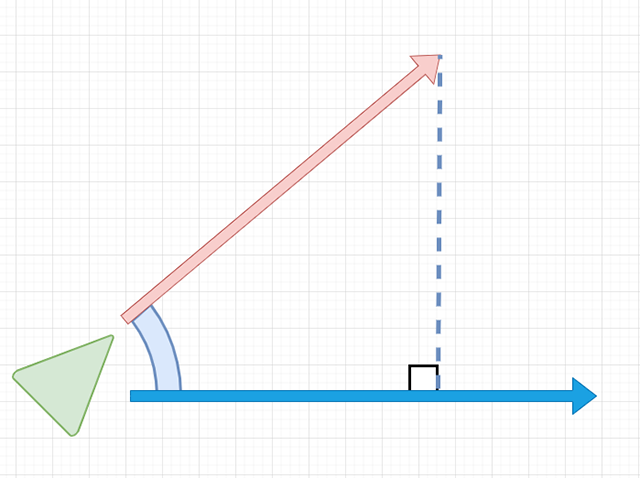
2つのベクトルの織りなす角度を考えるときは......
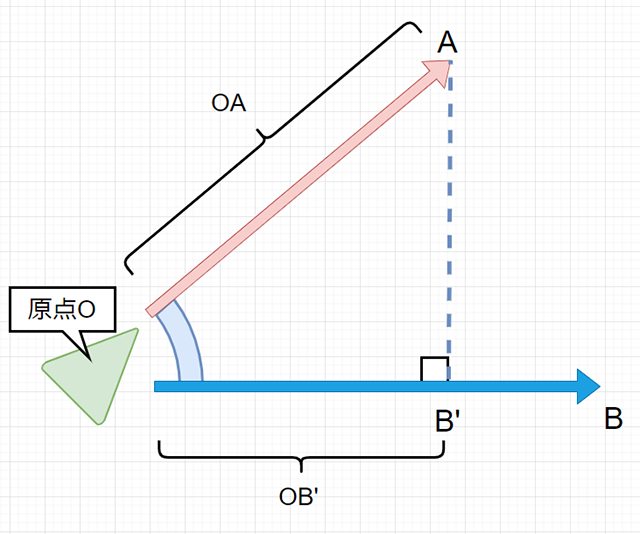
こんな感じで、直角三角形を考えます。
「辺OA」と「辺OB'」の長さがわかれば、
こんな感じで三角関数が使え、
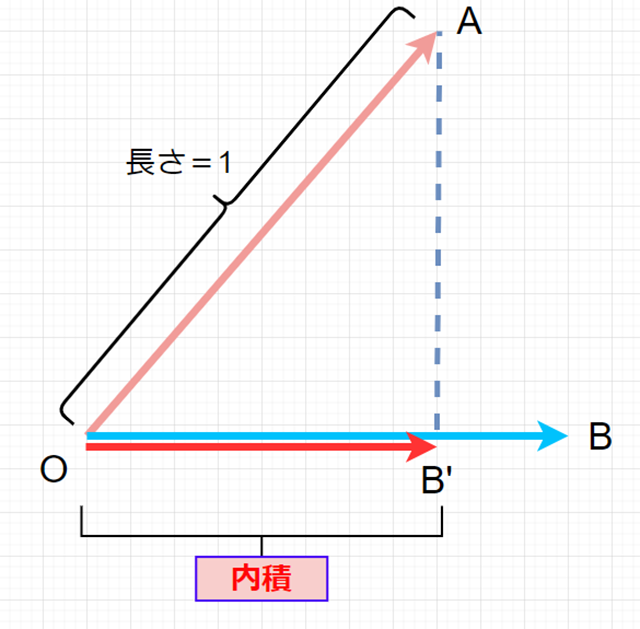
「cosΘ=OB'/OA」と表すことができるので、逆三角関数(アークコサイン)「acos」を使って角度Θを求めることが可能になります。ちなみに、「ベクトルA」は単位ベクトル、つまり「長さ=1」にしてあるので、
OB'/OA=OB'
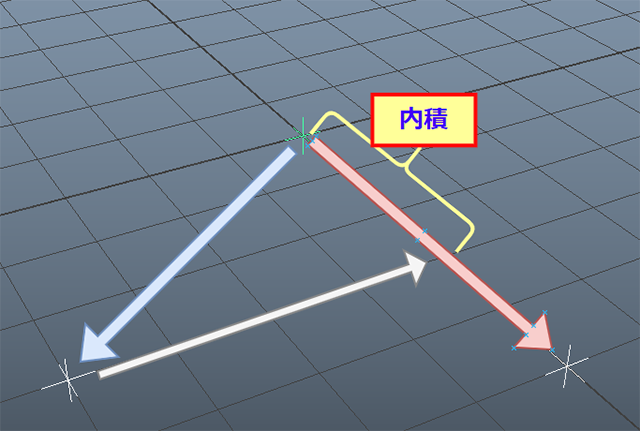
と置くことができますね。この辺から、あらかじめ「単位ベクトル」にしておいたことがジワジワと効いてくるわけです。さて、辺OAの長さは1とわかっていますが、辺OB'の長さは今のところ不明です。ここで使えるのが「ベクトルの内積」になります。
単位ベクトルAの内積は、下記の図のように......
点Aから垂直に下した点B'、すなわち「辺OB'」の長さを表します。
別の見方をすると、
「ベクトルA」を「ベクトルB」の向きに成分分解した際の長さ、と考えることもできます。MELコマンドには、このあたりの三角関数や内積を計算する便利なコマンドが揃っているので、上記のロジックさえ思いつけば実装は簡単です。
「ベクトルA」、「ベクトルB」の織りなす角度を計算するExpressionのコードは、こんな感じになります。
まず、内積でOB'の長さを求め、
float $dotProd = dot($defaultAimVector,$aimVector);
逆三角関数(アークコサイン)で2つのベクトルの織りなす角度を計算します。
float $rotateAngle = acosd($dotProd);
それぞれ1行で計算ができてしまいました。非常にお手軽ですね!
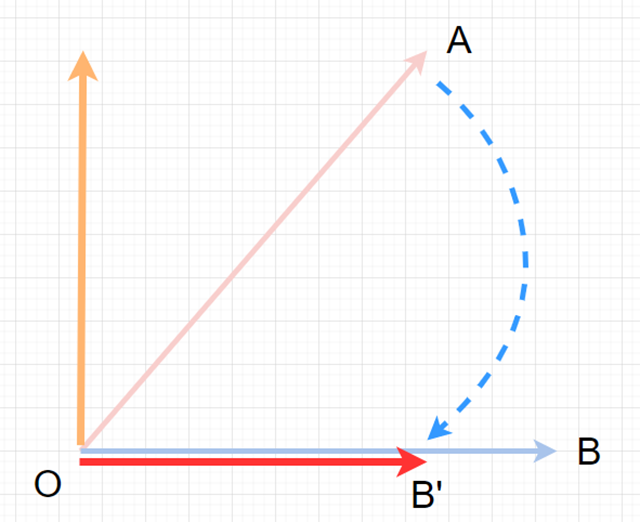
Step 03:回転軸を求める
Aim targetが動いたことによる回転角度は計算で求めることができました。では、いったいどの軸に沿って回転させたら良いのでしょうか。
Aim targetが動いたときの回転を図で考えてみると......
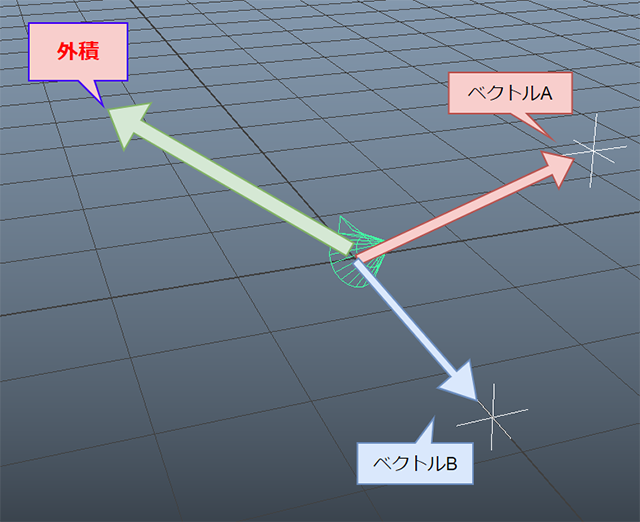
このように、「$defaultAimVector」から「$aimVector」にそれぞれ垂直な軸で回転させれば良さそうなイメージが見えると思います。2つのベクトルに垂直な軸、すなわち新たなベクトルを求めるにはどうしたら良いのでしょうか。ここでは、ズバリ「外積」を使います。
「外積」は正しく2つのベクトルに垂直なベクトルを計算する方法で、
ベクトルAとベクトルBの外積を計算すれば、回転軸となる新たなベクトルを計算で導き出すことができます。ここでも「MELコマンド」には外積を計算してくれる便利なコマンドがあるので、実装は非常にお手軽です。
回転軸を計算するExpressionは、
vector $rotateAxis = cross($defaultAimVector,$aimVector);
となります。
閑話休題:「外積」と「内積」......、混乱しそう?
さて、ここまでに「外積」と「内積」というキーワードが出てきましたが、どちらの計算ロジックが「外積」だったか「内積」だったか......、混乱しがちかもしれません。数式や文字、公式で覚えようとするとなかなか噛み合わずに苦労しますが、以下のような「非常に感覚的でグラフィカル」な覚え方はいかがでしょうか?
「内積」はこんな感じで、非常に「平面的な」イメージです。
一方、「外積は」こんな感じです。内積に対して非常に立体的なイメージが湧かないでしょうか? このイメージから、「内積は平面的に、内側に!」、「外積は立体的に、外にベクトルを出す!」といった印象をもてば、多少は混乱防止になるかもしれません。
え、強引ですか?
あぁ......、そう......ですか。
Step 04:axisとangleからEulerを求める
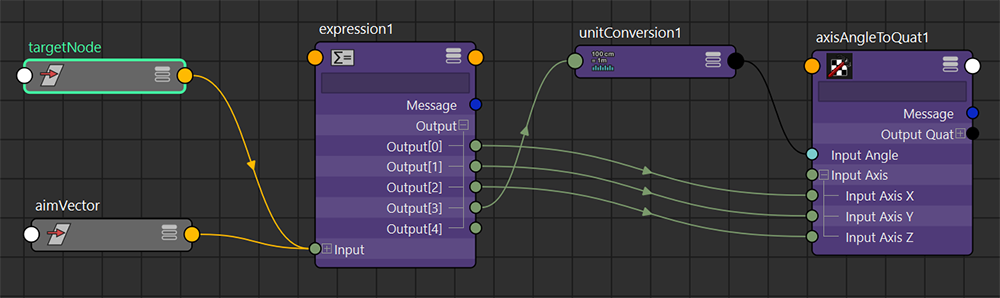
さて、以上でTargetNodeを回転させるのに十分な情報が取得できました。後は、この取得した回転情報と回転軸ベクトルをノードの回転情報に変換するだけです。ここは、MayaのUtilityNodeに回転軸と回転角度、すなわちaxisとangleからQuaternionを生成してくれる便利なノードがあるので、これを利用しましょう。
axisAngleToQuatノードがそれに当たります。axisAngleToQuatノードを作成後、Expressionからアトリビュートを接続します。
axisAngleToQuat1.inputAxisX = $rotateAxis.x;
axisAngleToQuat1.inputAxisY = $rotateAxis.y;
axisAngleToQuat1.inputAxisZ = $rotateAxis.z;
axisAngleToQuat1.inputAngle = $rotateAngle;
NodeEditorの見た目はこのようになります。
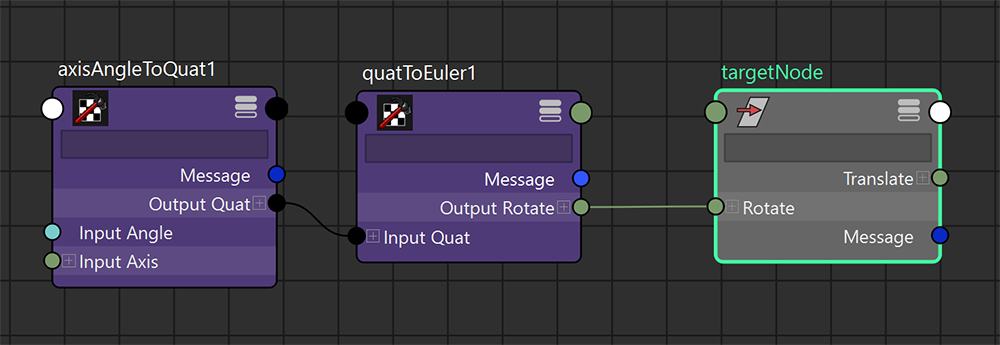
次にQuaternionをEulerに変換するノードです。
quatToEulerノードを作成して、接続しておきます。そして、結果のEulerをTargetNodeのRotationに戻すと......
できました! ハラショー!!
●Evaluationは「On demand」に!
そうそう。忘れてはいけないのが、Expressionの「Evaluation設定」です。
ここは必ず「On demand」に変えましょう。
規定では「Always」ですが、これでは毎フレーム必ずノード評価が行われてしまい、処理を圧迫しかねません。On demandにすることで、「Is dirty状態」になったときのみ処理が走るようになります。
[[SplitPage]]おまけ:MELの便利なコマンド「angle」
今回、数学の「グラフィカルな部分」の紹介ということで、回転角度の算出を三角関数と内積を使って計算しました。しかし、実は「angle」という便利なコマンドがMELにはあります。
float $rotateAngle = rad_to_deg(angle($defaultAimVector,$aimVector));
回転角度の取得は、この1行で計算が可能でした。
細かく見ていくと......
angle($defaultAimVector,$aimVector)
この部分で、すでに回転角度が算出できています。ただし、返ってくるのが「度」単位ではなく「ラジアン」なので、rad_to_degコマンドを通して「度」単位に変換させています。このように、MELには数学の演算コマンドが豊富に用意されているのです。
Maya公式ヘルプページからMELコマンドリファレンスを確認できますが、「数学」カテゴリのコマンド群にぜひ一度目を通すことをオススメします。
意外と新しい発見があるかもしれませんよ!
いかがでしょうか! これまで「数学」と聞くと、小難しい数式や意味不明なグラフを思い浮かべることが多かったのではないでしょうか。しかし、このように数値や数式の意味を別の側面で考えてみることで、意外にもグラフィカルな側面が強く見えてきたかと思います。
特に、ベクトルは「向き」と「長さ」をもつという特性から、その演算自体がグラフィカルな発想だなと思います。「数式」をイメージして問題を解くというより、「立体イメージを固めて解決していく」というアプローチに近いと私は感じています。
数学に対してグラフィックの側面からアプローチしてみると、「内積」、「外積」、「三関数」は小難しい数式や公式というイメージというよりも、パズルを解くためのピースを探し出してはめていく「便利ツール」のように見ることができるかもしれません。そう考えてみると「小難しい数学」のハードルが下がり、グラフィックアーティストでも触れそうな気がして来たりして......。
え? そうでもない? あぁ......そう、ですか......。
さて次回は話題を変えて、Photoshopに関するToolサポートのお話です。スタジオ COYOTE 3DCG STUDIO内で提供したPhotoshop用エクステンションToolの事例を基に、様々なTipsを紹介できればと思っております。
ではまた次回、
サヨナラ! サヨナラ! サヨナラ!!
Profile.
-

-
山本智人/Tomohito Yamamoto(COYOTE 3DCG STUDIO)
ゲーム開発会社にてグラフィックアーティストとして、モデリング・モーション・エフェクト・UIなどオールラウンドのグラフィック制作を経験後、テクニカルアーティストに転身。現在は株式会社クリーク・アンド・リバー社 COYOTE 3DCG STUDIOにて、社内外問わずアーティストのDCCツールサポートや制作パイプラインの提案・作成・運用を行う。特にアニメーション制御やモーション制作周りのテクニカルサポート・リガーとして様々なプロジェクトに従事