Step 02:2つのベクトルの織りなす角度を求める?
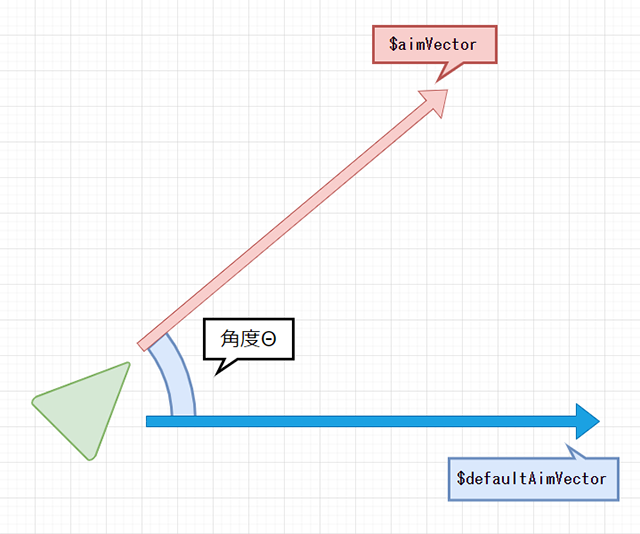
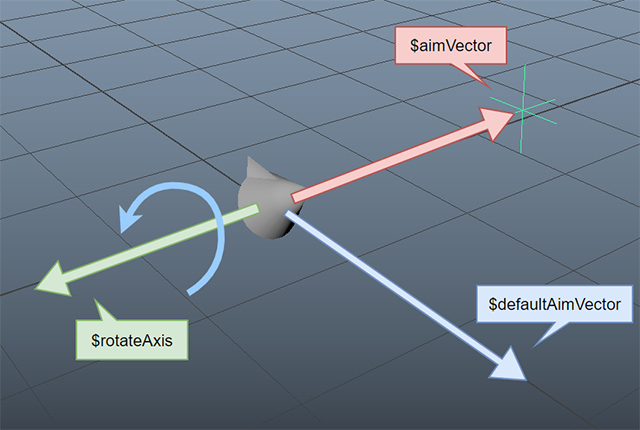
次に、現在の「$aimVector」の向きが初期値よりどの程度変化したかを見て、その回転角度を求めたいと思います。まず、もともとの「$aimVector」の値、すなわち初期値を定義します。
vector $defaultAimVector = <<1.0,0.0,0.0>>;
この初期値の定義は、状況に応じてふさわしい値を設定していくべきですが、ここではX軸方向を正面に向いている状態を初期値として定義しました。さて、この初期値のベクトル「$defaultAimVector」と、現在のベクトル「$aimVector」を比較し......
その2つのベクトルの織りなす角度を計算したいと思います。
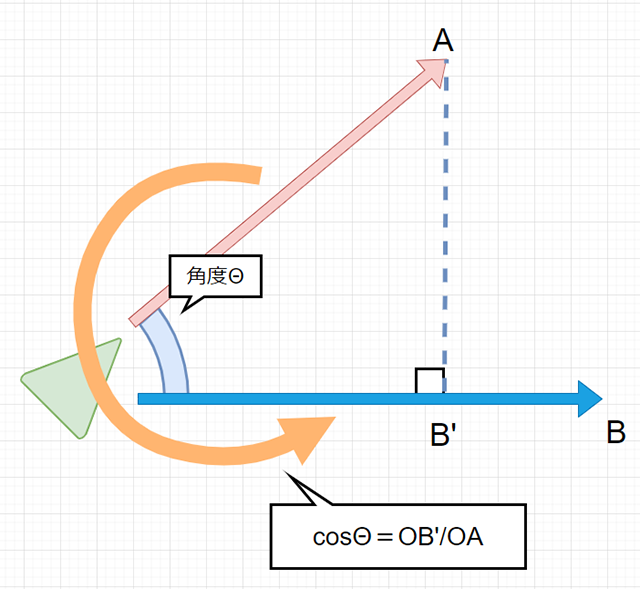
2つのベクトルの織りなす角度を考えるときは......
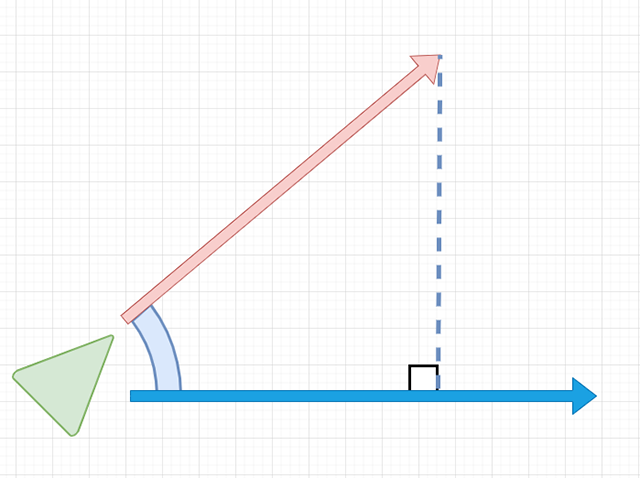
こんな感じで、直角三角形を考えます。
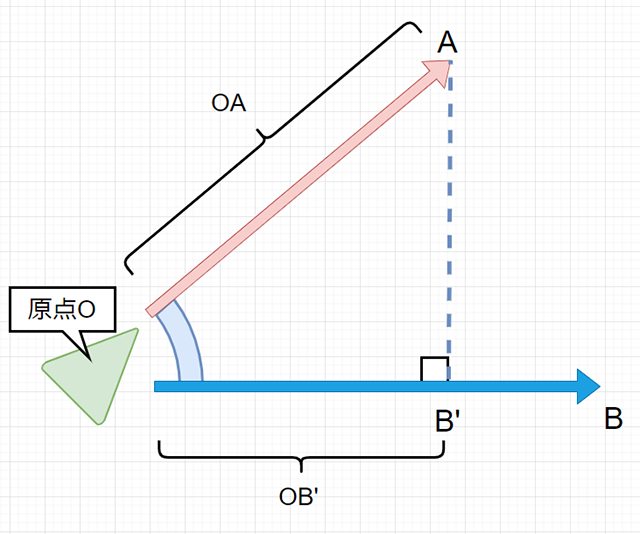
「辺OA」と「辺OB'」の長さがわかれば、
こんな感じで三角関数が使え、
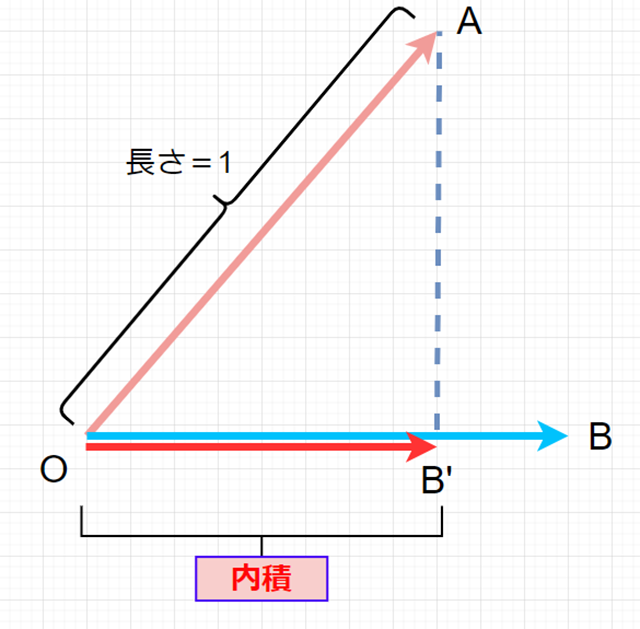
「cosΘ=OB'/OA」と表すことができるので、逆三角関数(アークコサイン)「acos」を使って角度Θを求めることが可能になります。ちなみに、「ベクトルA」は単位ベクトル、つまり「長さ=1」にしてあるので、
OB'/OA=OB'
と置くことができますね。この辺から、あらかじめ「単位ベクトル」にしておいたことがジワジワと効いてくるわけです。さて、辺OAの長さは1とわかっていますが、辺OB'の長さは今のところ不明です。ここで使えるのが「ベクトルの内積」になります。
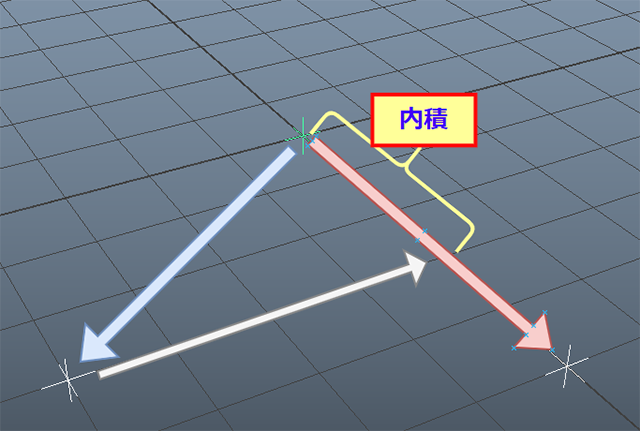
単位ベクトルAの内積は、下記の図のように......
点Aから垂直に下した点B'、すなわち「辺OB'」の長さを表します。
別の見方をすると、
「ベクトルA」を「ベクトルB」の向きに成分分解した際の長さ、と考えることもできます。MELコマンドには、このあたりの三角関数や内積を計算する便利なコマンドが揃っているので、上記のロジックさえ思いつけば実装は簡単です。
「ベクトルA」、「ベクトルB」の織りなす角度を計算するExpressionのコードは、こんな感じになります。
まず、内積でOB'の長さを求め、
float $dotProd = dot($defaultAimVector,$aimVector);
逆三角関数(アークコサイン)で2つのベクトルの織りなす角度を計算します。
float $rotateAngle = acosd($dotProd);
それぞれ1行で計算ができてしまいました。非常にお手軽ですね!
Step 03:回転軸を求める
Aim targetが動いたことによる回転角度は計算で求めることができました。では、いったいどの軸に沿って回転させたら良いのでしょうか。
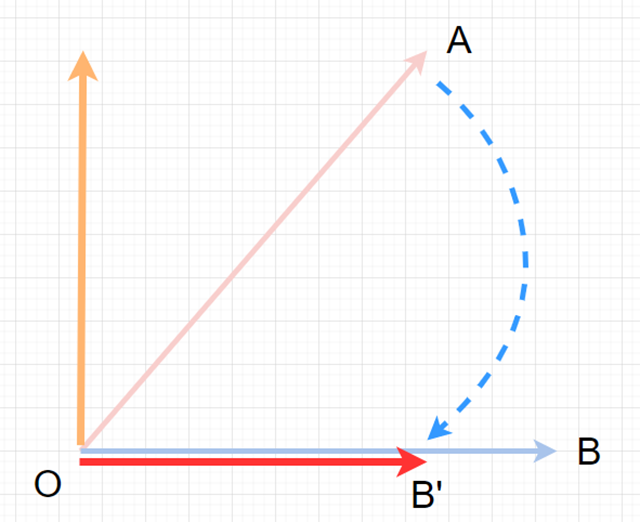
Aim targetが動いたときの回転を図で考えてみると......
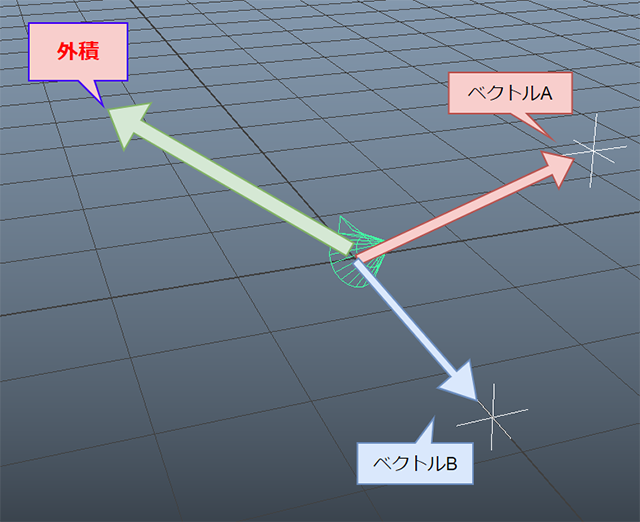
このように、「$defaultAimVector」から「$aimVector」にそれぞれ垂直な軸で回転させれば良さそうなイメージが見えると思います。2つのベクトルに垂直な軸、すなわち新たなベクトルを求めるにはどうしたら良いのでしょうか。ここでは、ズバリ「外積」を使います。
「外積」は正しく2つのベクトルに垂直なベクトルを計算する方法で、
ベクトルAとベクトルBの外積を計算すれば、回転軸となる新たなベクトルを計算で導き出すことができます。ここでも「MELコマンド」には外積を計算してくれる便利なコマンドがあるので、実装は非常にお手軽です。
回転軸を計算するExpressionは、
vector $rotateAxis = cross($defaultAimVector,$aimVector);
となります。
閑話休題:「外積」と「内積」......、混乱しそう?
さて、ここまでに「外積」と「内積」というキーワードが出てきましたが、どちらの計算ロジックが「外積」だったか「内積」だったか......、混乱しがちかもしれません。数式や文字、公式で覚えようとするとなかなか噛み合わずに苦労しますが、以下のような「非常に感覚的でグラフィカル」な覚え方はいかがでしょうか?
「内積」はこんな感じで、非常に「平面的な」イメージです。
一方、「外積は」こんな感じです。内積に対して非常に立体的なイメージが湧かないでしょうか? このイメージから、「内積は平面的に、内側に!」、「外積は立体的に、外にベクトルを出す!」といった印象をもてば、多少は混乱防止になるかもしれません。
え、強引ですか?
あぁ......、そう......ですか。
Step 04:axisとangleからEulerを求める
さて、以上でTargetNodeを回転させるのに十分な情報が取得できました。後は、この取得した回転情報と回転軸ベクトルをノードの回転情報に変換するだけです。ここは、MayaのUtilityNodeに回転軸と回転角度、すなわちaxisとangleからQuaternionを生成してくれる便利なノードがあるので、これを利用しましょう。
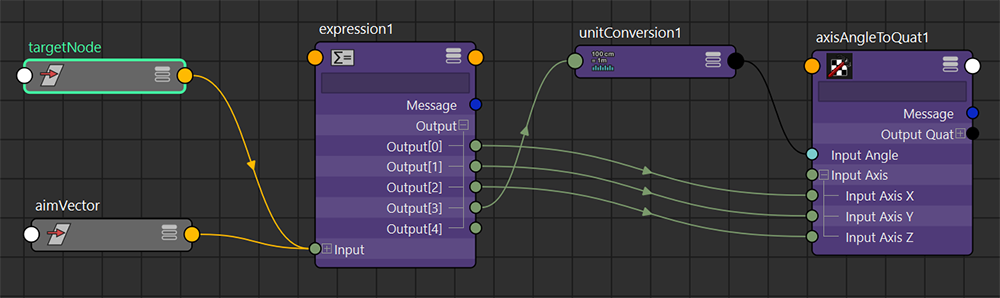
axisAngleToQuatノードがそれに当たります。axisAngleToQuatノードを作成後、Expressionからアトリビュートを接続します。
axisAngleToQuat1.inputAxisX = $rotateAxis.x;
axisAngleToQuat1.inputAxisY = $rotateAxis.y;
axisAngleToQuat1.inputAxisZ = $rotateAxis.z;
axisAngleToQuat1.inputAngle = $rotateAngle;
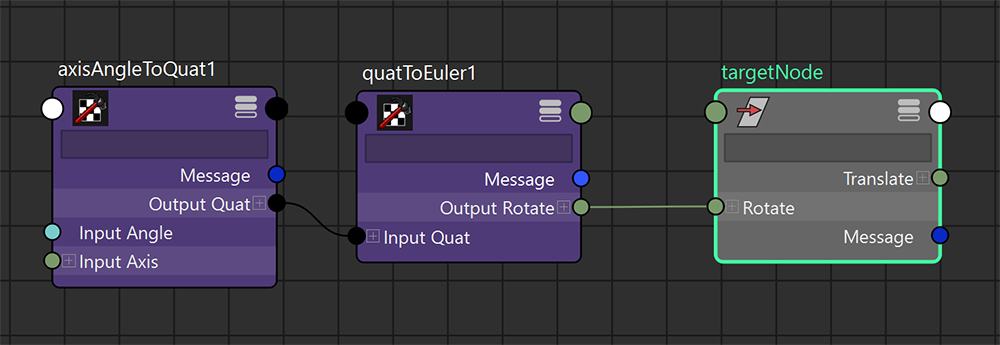
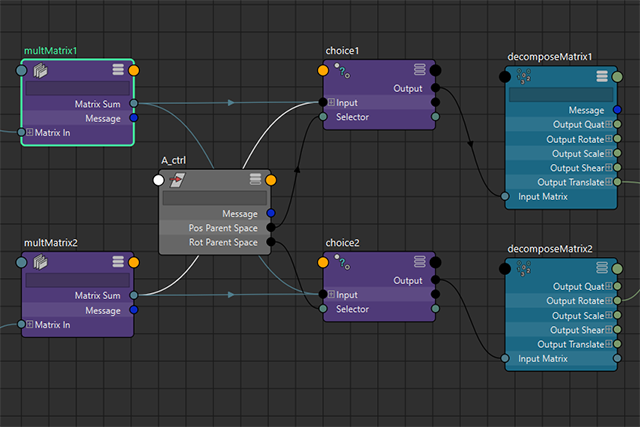
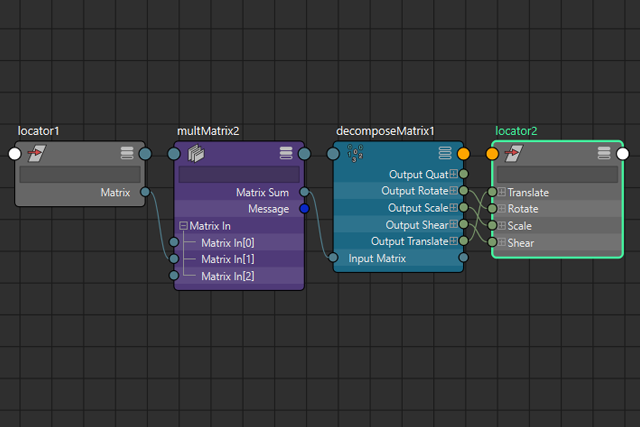
NodeEditorの見た目はこのようになります。
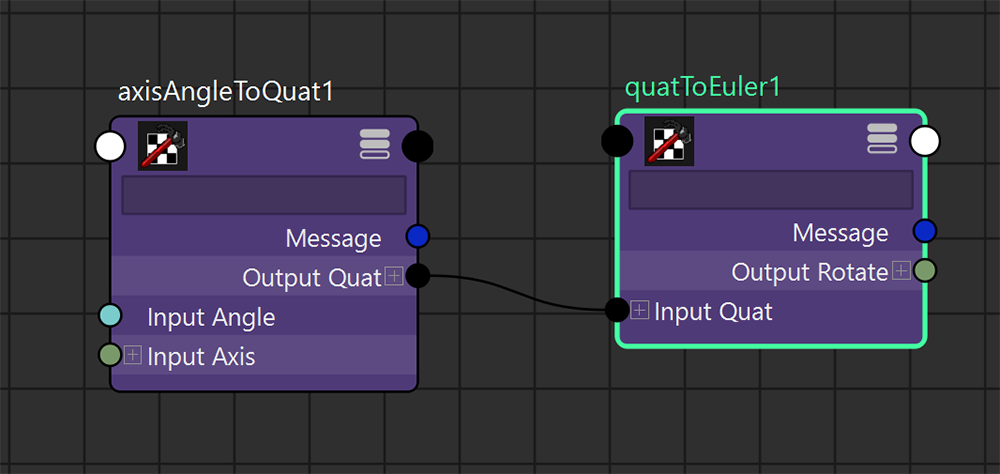
次にQuaternionをEulerに変換するノードです。
quatToEulerノードを作成して、接続しておきます。そして、結果のEulerをTargetNodeのRotationに戻すと......
できました! ハラショー!!
●Evaluationは「On demand」に!
そうそう。忘れてはいけないのが、Expressionの「Evaluation設定」です。
ここは必ず「On demand」に変えましょう。
規定では「Always」ですが、これでは毎フレーム必ずノード評価が行われてしまい、処理を圧迫しかねません。On demandにすることで、「Is dirty状態」になったときのみ処理が走るようになります。