クリーク・アンド・リバー社の社内CGスタジオであり、ゲームの3DCGグラフィックス制作を中心に手がけているCOYOTE 3DCG STUDIO。本連載では、同社のTAチームによる制作に役立つ技術TIPSを紹介していく。
TEXT_山本智人 / Tomohito Yamamoto(COYOTE 3DCG STUDIO)
EDIT_三村ゆにこ / Uniko Mimura(@UNIKO_LITTLE)
はじめに
おはこんばんちわ、COYOTE 3DCG STUDIOテクニカルアーティストの山本です。
前回の記事では、Matrixを使った親空間切り替えリグの実装について紹介しました。今回はMatrixの応用編として、Matrixを使ってモーションやポーズの反転を行なってみようと思います。
モーションやポーズの反転は、モーションの作業工数を大きく下げることができる有効な手段で、以前当社のブログTECH-COYOTE 「マトリクスを使ったポーズ・モーションの左右反転」でも紹介しました。こちらの記事では、Xでマイナススケール反転を掛けたMatrixを基のMatrixに乗算し、Transformや回転成分はQuaternionを取り出してノードに戻すという手法で実現していました。
今回はそれとは異なるアプローチとして、「Matrixとベクトルを組み合わせた手法」を探ってみたいと思います。
Results:結果を先に
1:
対象のノードに対してaimVectorとupVectorを定義するMatrixを用意し、対象ノードのMatrixを乗じて対象ノードの姿勢を表すベクトルを生成
2:生成したベクトルを反転して回転成分に変換
3:反転した移動成分と共に、上記で反転した回転成分をノードに戻す
このようにして、Matrixとベクトルをベースに姿勢の反転計算を実現しました。では、順を追ってそのロジックを紐解いてみましょう。
Step 01:反転について考えてみる
まず「ポーズの反転」について少し考察してみましょう。
移動値の反転は「原点」を基準として考えれば、反転したい軸方向に [-1] を乗じた値がそれにあたる、ということは容易に想像できると思います。
では回転はどうでしょうか? 左右反転ならY軸の回転にマイナスを乗算すれば良いだけでしょうか?
残念ながら、Y軸回転のみを反転させたところで理想の結果は得られないことが多いです。このことは、前述の当社ブログ記事でも解説していますが、回転成分にオイラー回転を用いていることが原因の1つで、以前の記事「Tips01:【Maya】ベクトルでBend制御してみよう」で紹介した通り、姿勢制御においてオイラー回転は不向きなことがあります。
ではどのように回転や姿勢を表現したら良いのでしょうか。
考え方の1つとして「ベクトル」があります。先ほどの「移動値の反転」の考察でもわかるように、「空間座標」の反転は非常にシンプルで容易です。対象のノードの向きや回転を三次元ベクトルとして考えることで、現在の姿勢を空間座標で表すことができるため、姿勢の反転が容易になるはずです。
Step 02:現在の姿勢をベクトルで表してみよう
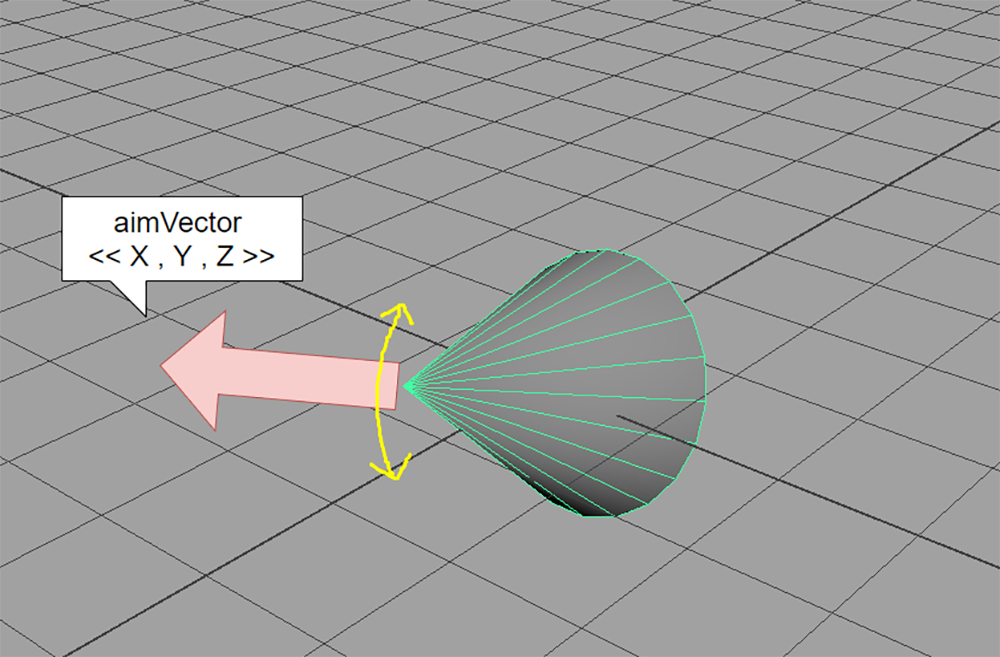
現在の向きを表すには、前述の「ベクトルのBend制御」の記事でも紹介したように、回転成分を「曲げ = Bend」と「捻り = Roll」に分解して考えるのがシンプルです。
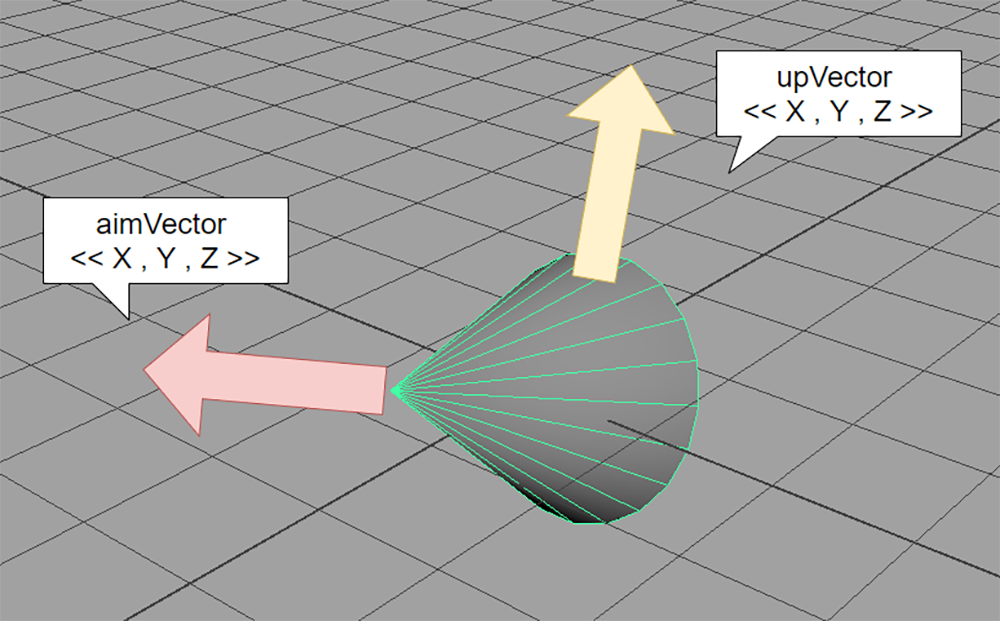
Bend成分はノードの「MainAxis」のベクトル(すなわち「aimVector」)で表すことができ、
Roll成分はノードの「SecondaryAxis」のベクトル(すなわち「upVector」)で表すことができます。
Step 03:Matrixの計算で、aimVectorとupVectorを求める
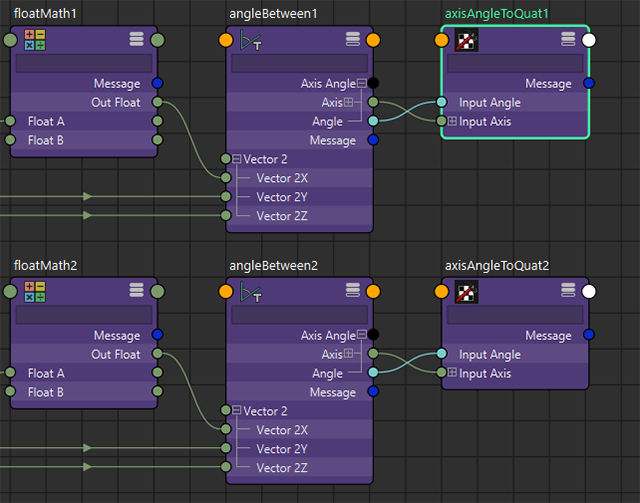
NodeEditor上で、これらのaimVectorとupVectorを計算してみましょう。ここでは、aimVectorを [1.0,0.0,0.0]、upVectorを [0.0,1.0,0.0] とします。
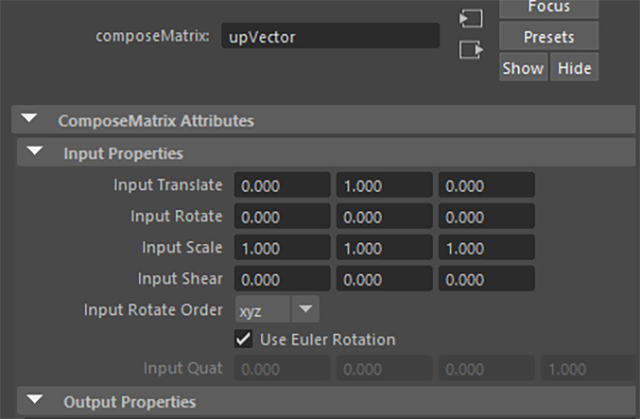
これらをMatrix計算するのに、aimVector用/upVector用で2つのComposeMatrixノードを用意し、それぞれinputTransformの値に [1.0,0.0,0.0]、[0.0,1.0,0.0] の値を入力しておきます。
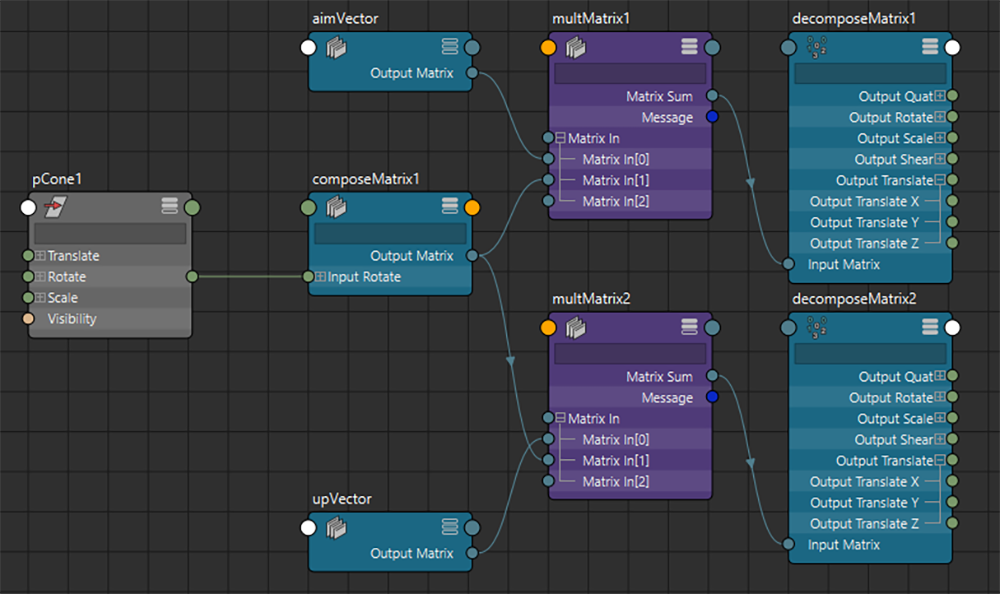
これらを対象のノードのオイラー回転から生成したMatrixに乗算し、decomposeMatrixを介して移動座標を取り出すことで、回転後のaimVectorとupVectorを取得することができます。
回転成分から生成したMatrixを使うことで移動成分などを除外し、回転成分のみを評 価することができます。
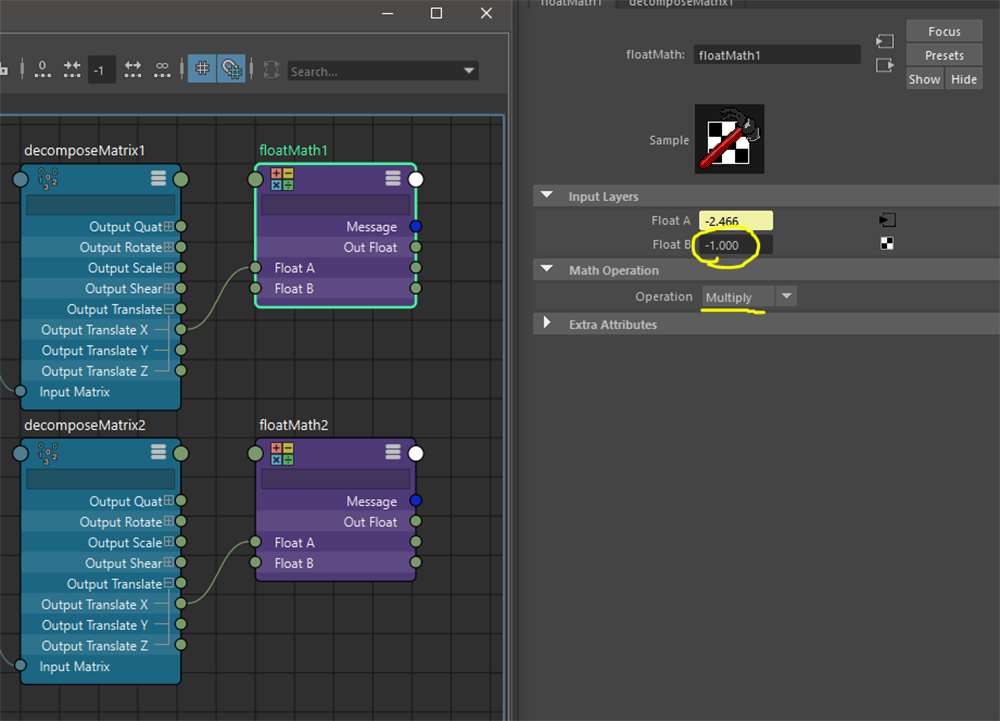
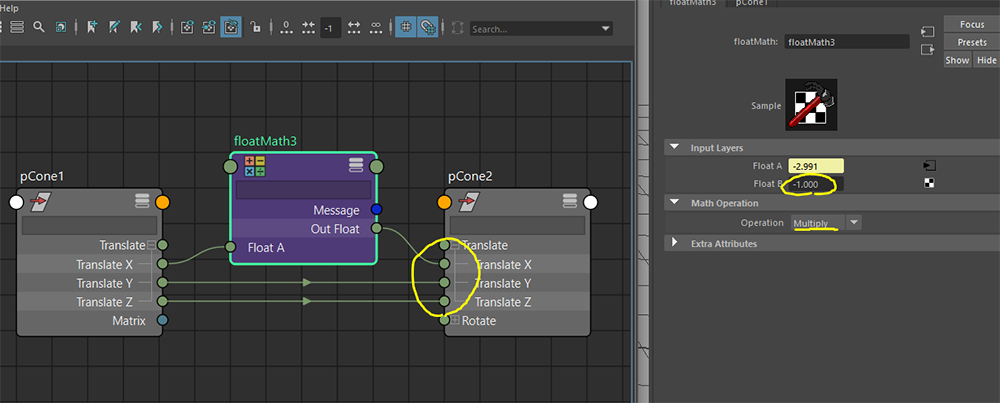
後は取得後のベクトルをミラーさせればOK。
今回は左右反転を行うので、X軸方向に [-1.0] を乗算させておきましょう。
Step 04:反転したベクトルから求めた回転成分の合成を行なってみよう
回転成分の合成にはQuaternionを使います。
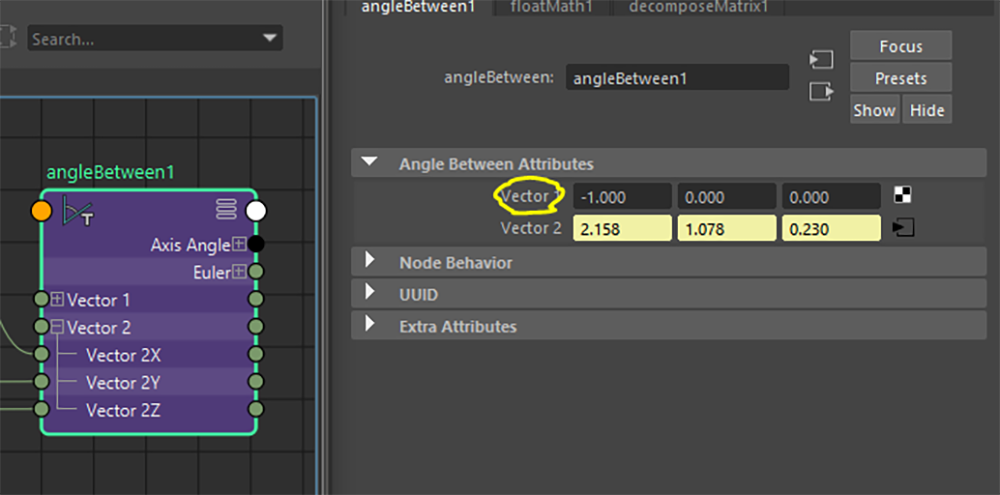
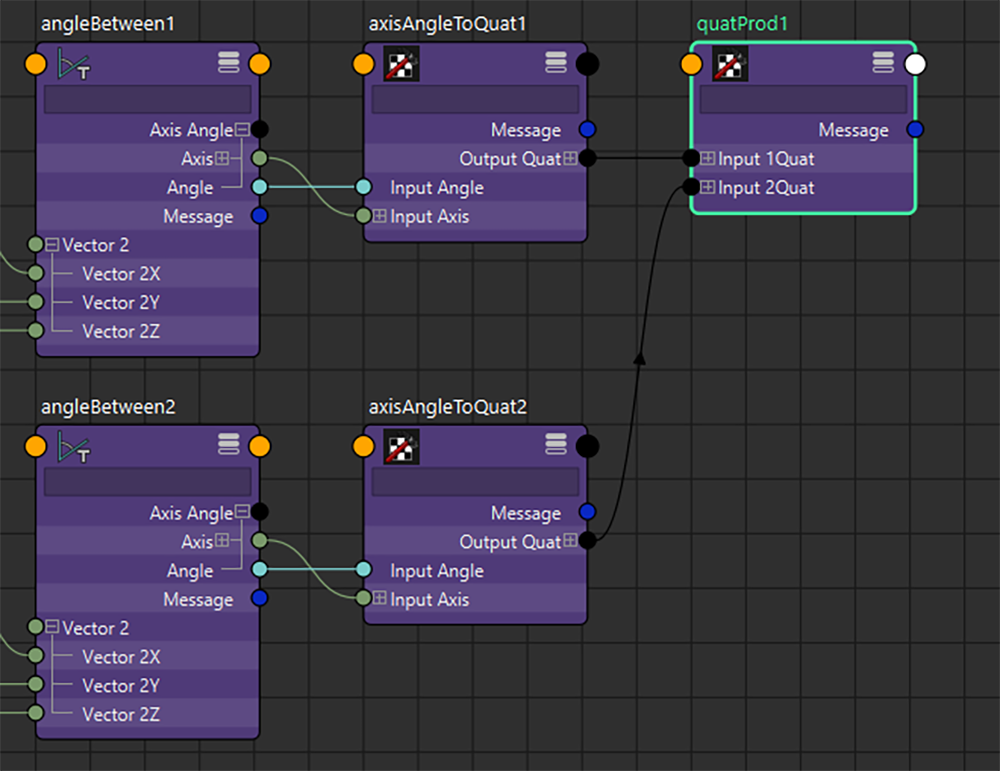
取得したそれぞれのベクトルをいったん 「angleBetweenノード」に繋ぎ、
[Vector 1] はそれぞれ、ノードが初期位置のときのベクトルの値を入れておきます。一次的に対象ノードを初期位置に戻すか、回転する前に [Vector 1] に接続してから接続を解除するなどして、値を設定できます。
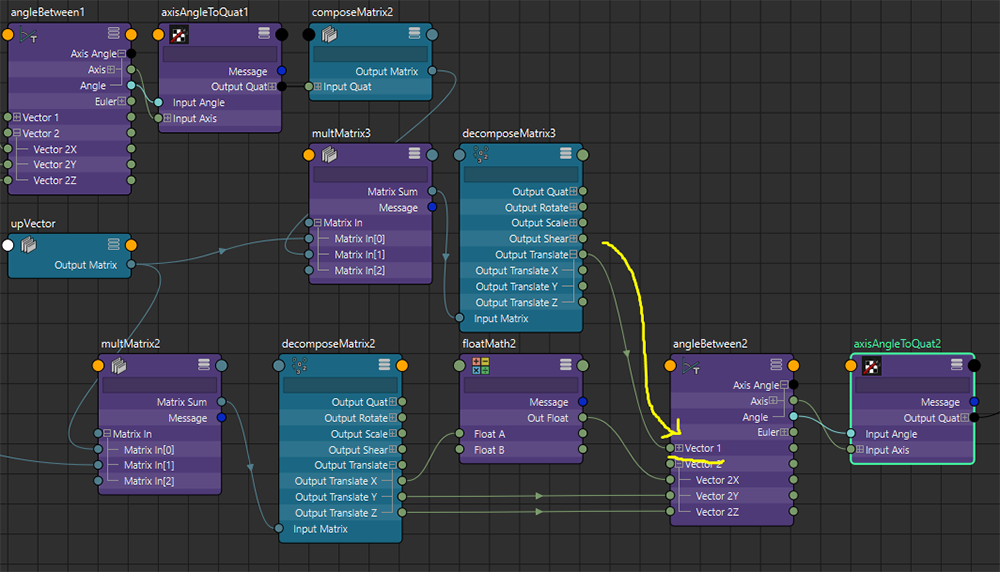
ここで注意が必要なのは、upVector側のangleBetweenノードの [Vector 1] の値はまだ操作しない、ということです。この後、回転のBend成分とRoll成分を合成するのですが、現状では......
上記NodeEditorの箇所で取得できる、回転後のupVectorの成分はBend成分も含まれたものです。回転順序的にBend回転した後にRollさせたいので、回転基準となる [Vector 1] には、「あらかじめBend成分で回転させたupVectorの初期値」を設定したいのです。
さて、Roll成分の処理は後で組み込むとして、ひとまず回転成分をQuaternionに変換します。
「axisAngleToQuatノード」を生成して、angleBetweenノードの [Axis] と [Angle] をそれぞれ接続します。これでBend成分の回転成分であるQuaternionが計算できたはずです。
では、先ほど触れたRoll成分の計算に移ります。
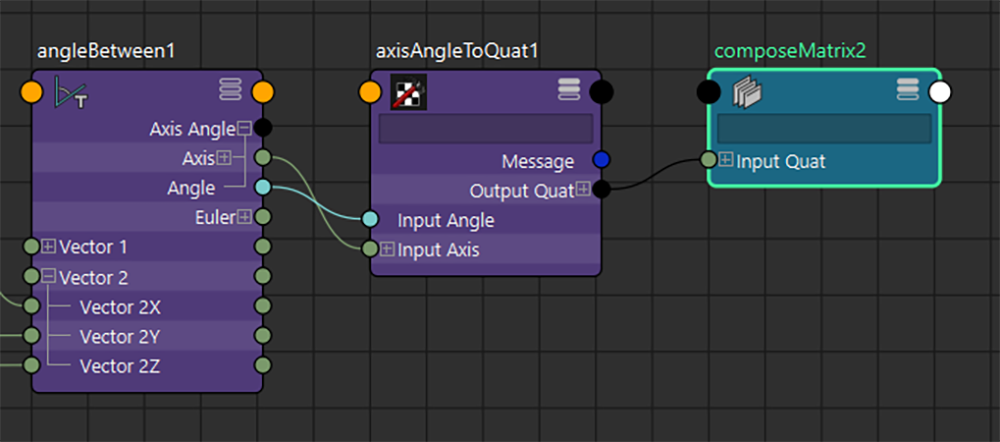
Bend成分のQuaternionを「composeMatrixノード」に接続して、回転マトリクスを生成します。次に、この回転MatrixにupVectorで与えたベクトルと同じベクトルをMatrixに変換し、同様に乗算して回転させます。
これで、まだRoll成分を加味していない状態のupVectorの成分が計算できました。
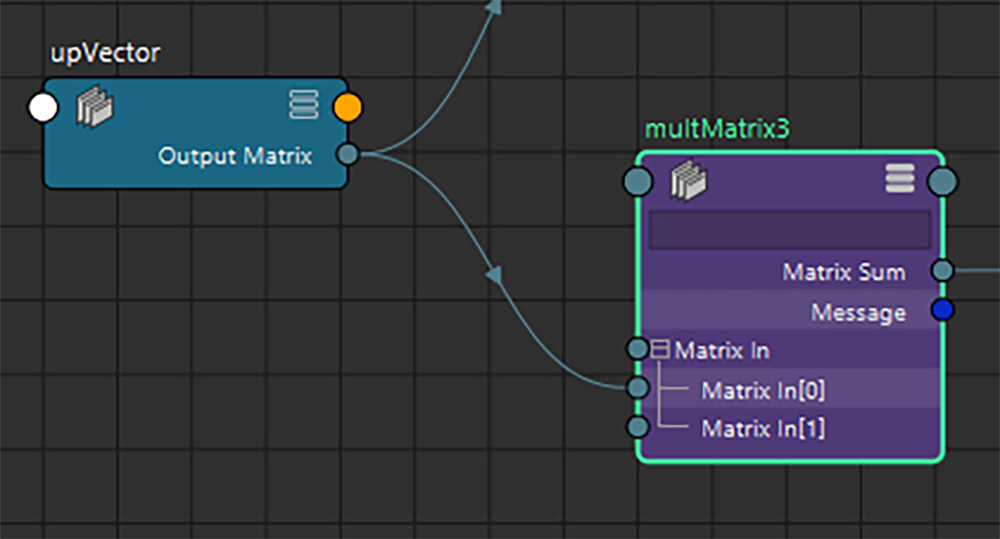
このMatrixを「decomposeMatrixノード」に接続して移動成分を取り出し、upVector側にあるangleBetweenノードの回転基準となるベクトル、すなわち [Vector 1] に接続します。
これで正しくRoll成分を評価できるようになったはずです。
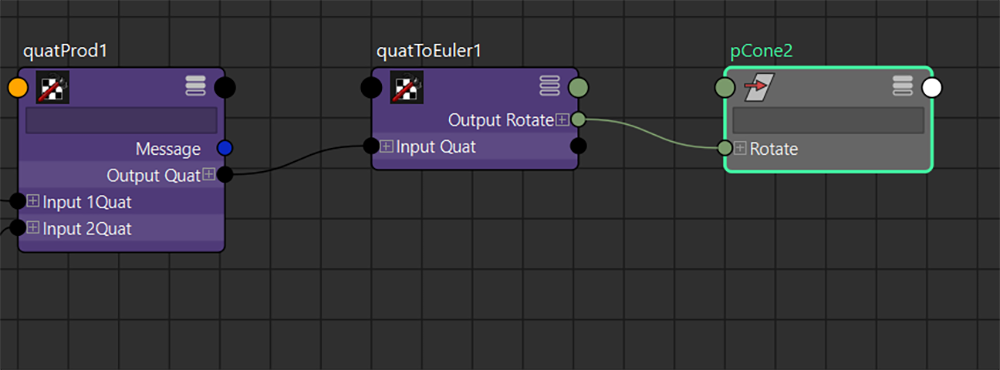
そして「quatProdノード」を生成して、それぞれBend成分のQuaternionとRoll成分のQuaternionを乗算します。以上で、反転した回転成分が計算できたはずです。
では、試しに別のノードを作って接続させて確認してみましょう。
「quatToEulerノード」を用いて回転成分をオイラーに戻し、ノードの [Rotate] に接続、
移動成分「X」に対して [-1] を乗算してノードに接続してみます。
すると......
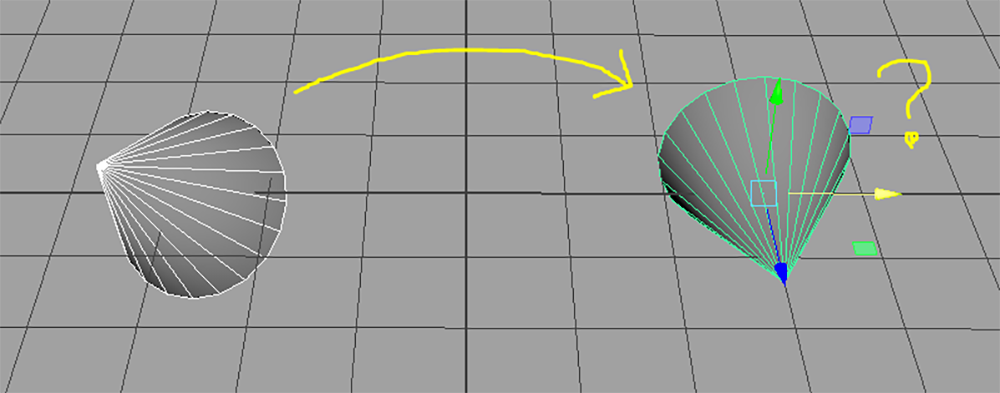
このとおり! きれいに左右対称に動いていることが確認できます。
Step 05:実際にやってみよう
ここまでのロジックを実際のアニメーションに適用して、その効果を確かめてみましょう。基のアニメーションはこんな感じです。
アニメーションはMaya 2022に付属している「MotionLibrary」より適当な歩行モーションをインポートして、キャラクターにリターゲット。キャラクターは当スタジオで作成したVRChat向けモデルのミュリシアちゃんを使っています。
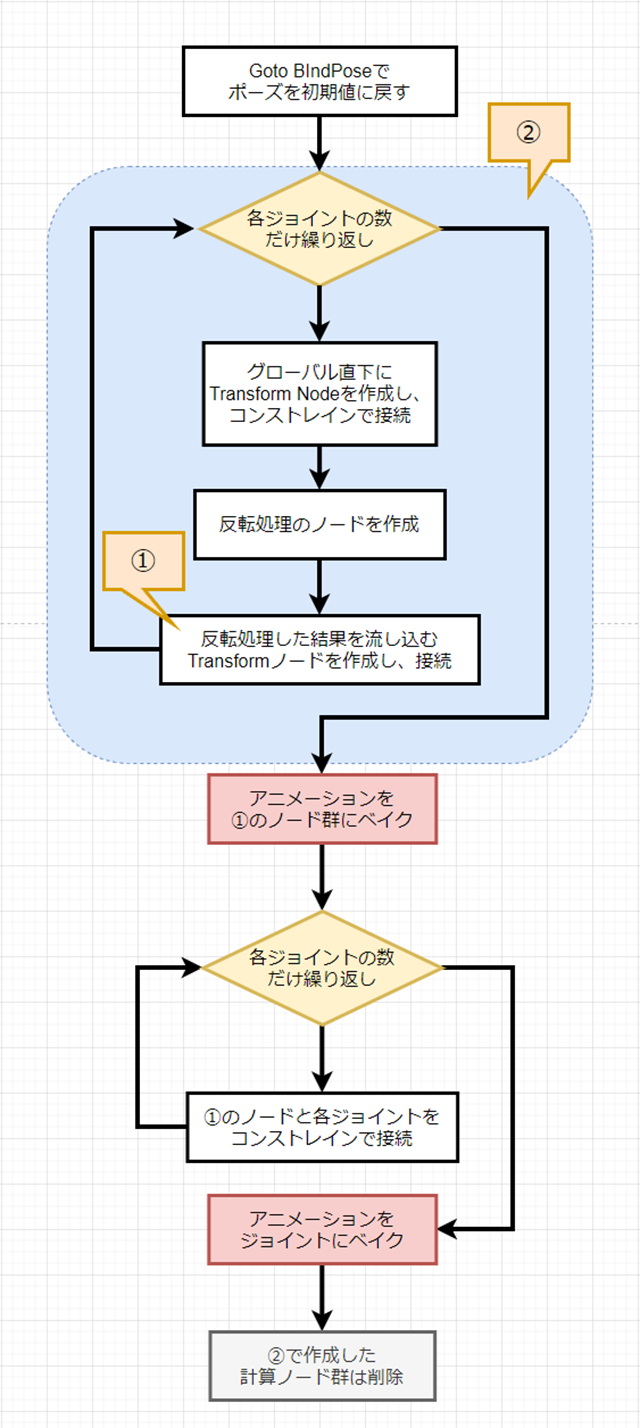
処理のフローは以下の通り。
「Step 03」までで確認したロジックは、あくまでも「グローバル挙動を行うノード」に対しての処理なので、いったん全ての対象ノードの挙動をグローバルに出したノードにベイクし、ミラー処理を行い再度ノードに戻す、という点がミソです。
では順にPythonで書いてみましょう。
まず初期ポーズに戻してから、各対象ノード(ここではキャラクターの全てのジョイント)ごとにグローバル直下に「Transformノード」を作り、コンストレインで接続します。
import maya.cmds as cmds
import maya.mel as mel
#処理させたいノードのルートをあらかじめ選択して実行する前提で、選択からジョイントのルートを取得
rootNode = cmds.ls(sl = True)[0]
mel.eval('GoToBindPose;')
jointList = cmds.ls(rootNode,dag = True,type = 'joint')
inputLocList = []
culNodeList = []
outputLocDict = {}
outputOffsetList = []
#各ジョイントごとの処理
for j in jointList:
#あらかじめ反転対象のジョイントを探しておく
mirrorJoint = j
if 'Left' in j:
mirrorJoint = j.replace('Left','Right')
elif 'Right' in j:
mirrorJoint = j.replace('Right','Left')
if not mirrorJoint in jointList:
#ミラー対象が見当たらなければ処理をスキップ
continue
#各ジョイントごとにTransformノードを作り、コンストレインで接続
loc = cmds.createNode('transform')
inputLocList.append(loc)
#移動・回転に0.0をセットすることで初期位置に戻れるようにoffsetノードを用意
cmds.pointConstraint(j,loc)
cmds.orientConstraint(j,loc,mo = True)
このとき、前述のミラーを取得するノード構造を構築して、初期のベクトル値についても登録しておきます。
#反転ベクトルを生成するためのノード群を作成
rotateMatrix = cmds.createNode('composeMatrix')
aimVectorNode = cmds.createNode('composeMatrix')
upVectorNode = cmds.createNode('composeMatrix')
aimVectorMatrix = cmds.createNode('multMatrix')
upVectorMatrix = cmds.createNode('multMatrix')
aimVectorDecomposeMatrix = cmds.createNode('decomposeMatrix')
upVectorDecomposeMatrix = cmds.createNode('decomposeMatrix')
mirrorAimVector = cmds.createNode('floatMath')
mirrorUpVector = cmds.createNode('floatMath')
getBendAxisAngle = cmds.createNode('angleBetween')
getRollAxisAngle = cmds.createNode('angleBetween')
getBendQuat = cmds.createNode('axisAngleToQuat')
getRollQuat = cmds.createNode('axisAngleToQuat')
getBendMatrix = cmds.createNode('composeMatrix')
getBendedOrgUpVector = cmds.createNode('multMatrix')
bendedUpVectorDecomposeMatrix = cmds.createNode('decomposeMatrix')
quatCul = cmds.createNode('quatProd')
quatToE = cmds.createNode('quatToEuler')
mirrorPosNode = cmds.createNode('floatMath')
culNodeList.extend([rotateMatrix,aimVectorNode,upVectorNode,
aimVectorMatrix,upVectorMatrix,
aimVectorDecomposeMatrix,upVectorDecomposeMatrix, mirrorAimVector,mirrorUpVector,
getBendAxisAngle,getRollAxisAngle,
getBendQuat,getRollQuat,
getBendMatrix,getBendedOrgUpVector,bendedUpVectorDecomposeMatrix,
quatCul,quatToE,mirrorPosNode])
#反転マトリクスのノード構築
cmds.connectAttr('{}.rotate'.format(loc),'{}.inputRotate'.format(rotateMatrix))
#aimVector/upVectorの定義
cmds.setAttr('{}.inputTranslate'.format(aimVectorNode),1.0,0.0,0.0) cmds.setAttr('{}.inputTranslate'.format(upVectorNode),0.0,1.0,0.0)
cmds.connectAttr('{}.outputMatrix'.format(aimVectorNode),'{}.matrixIn[0]'.format(aimVectorMatrix))
cmds.connectAttr('{}.outputMatrix'.format(upVectorNode),'{}.matrixIn[0]'.format(upVectorMatrix))
cmds.connectAttr('{}.outputMatrix'.format(rotateMatrix),'{}.matrixIn[1]'.format(aimVectorMatrix))
cmds.connectAttr('{}.outputMatrix'.format(rotateMatrix),'{}.matrixIn[1]'.format(upVectorMatrix))
cmds.connectAttr('{}.matrixSum'.format(aimVectorMatrix),'{}.inputMatrix'.format(aimVectorDecomposeMatrix))
cmds.connectAttr('{}.matrixSum'.format(upVectorMatrix),'{}.inputMatrix'.format(upVectorDecomposeMatrix))
cmds.connectAttr('{}.outputTranslateX'.format(aimVectorDecomposeMatrix),'{}.floatA'.format(mirrorAimVector))
cmds.connectAttr('{}.outputTranslateX'.format(upVectorDecomposeMatrix),'{}.floatA'.format(mirrorUpVector))
#ベクトル反転floatMathノードの値を操作
cmds.setAttr('{}.floatB'.format(mirrorAimVector),-1.0)
cmds.setAttr('{}.floatB'.format(mirrorUpVector),-1.0)
cmds.setAttr('{}.operation'.format(mirrorAimVector),2)
cmds.setAttr('{}.operation'.format(mirrorUpVector),2)
#bend成分のベクトル接続
cmds.connectAttr('{}.outFloat'.format(mirrorAimVector),'{}.vector2X'.format(getBendAxisAngle))
cmds.connectAttr('{}.outputTranslateY'.format(aimVectorDecomposeMatrix),'{}.vector2Y'.format(getBendAxisAngle))
cmds.connectAttr('{}.outputTranslateZ'.format(aimVectorDecomposeMatrix),'{}.vector2Z'.format(getBendAxisAngle))
#aimVectorの規定値を現在のvector2の値から一時的にコネクションして切断し、値を設定する。
cmds.connectAttr('{}.vector2'.format(getBendAxisAngle),'{}.vector1'.format(getBendAxisAngle))
cmds.disconnectAttr('{}.vector2'.format(getBendAxisAngle),'{}.vector1'.format(getBendAxisAngle))
#Roll成分のベクトル接続 ※vector1はまだ。
cmds.connectAttr('{}.outFloat'.format(mirrorUpVector),'{}.vector2X'.format(getRoll AxisAngle))
cmds.connectAttr('{}.outputTranslateY'.format(upVectorDecomposeMatrix),'{}.vector2Y'.format(getRollAxisAngle))
cmds.connectAttr('{}.outputTranslateZ'.format(upVectorDecomposeMatrix),'{}.vector2Z'.format(getRollAxisAngle))
#Quaternion取得
cmds.connectAttr('{}.axis'.format(getBendAxisAngle),'{}.inputAxis'.format(getBendQ uat))
cmds.connectAttr('{}.angle'.format(getBendAxisAngle),'{}.inputAngle'.format(getBen dQuat))
cmds.connectAttr('{}.axis'.format(getRollAxisAngle),'{}.inputAxis'.format(getRollQ uat))
cmds.connectAttr('{}.angle'.format(getRollAxisAngle),'{}.inputAngle'.format(getRol lQuat))
#Roll成分の回転基準のベクトルを計算
cmds.connectAttr('{}.outputQuat'.format(getBendQuat),'{}.inputQuat'.format(getBend Matrix))
cmds.setAttr('{}.useEulerRotation'.format(getBendMatrix),False)
cmds.connectAttr('{}.outputMatrix'.format(upVectorNode),'{}.matrixIn[0]'.format(getBendedOrgUpVector))
cmds.connectAttr('{}.outputMatrix'.format(getBendMatrix),'{}.matrixIn[1]'.format(getBendedOrgUpVector))
cmds.connectAttr('{}.matrixSum'.format(getBendedOrgUpVector),'{}.inputMatrix'.format(bendedUpVectorDecomposeMatrix))
#upVectorの回転計算の基準ベクトルVector1にコネクション
cmds.connectAttr('{}.outputTranslate'.format(bendedUpVectorDecomposeMatrix),'{}.vector1'.format(getRollAxisAngle))
ソースは長いですが、要は前述のノードエディタの構造を作っているだけですね。出力用のノードを作ってコネクションした後、ジョイントからのアニメーションをベイクします。
#出力用のノードのコネクション
#出力用ノードはオフセット用ノードとあらかじめ二重構造にしておく
outputNode_offset = cmds.createNode('transform')
outputOffsetList.append(outputNode_offset)
outputNode = cmds.createNode('transform')
cmds.parent(outputNode,outputNode_offset)
outputLocDict[j] = outputNode
cmds.connectAttr('{}.outputQuat'.format(getBendQuat),'{}.input1Quat'.format(quatCul))
cmds.connectAttr('{}.outputQuat'.format(getRollQuat),'{}.input2Quat'.format(quatCul))
cmds.connectAttr('{}.outputQuat'.format(quatCul),'{}.inputQuat'.format(quatToE))
#接続はoffsetノードの方に。
#回転出力の接続
cmds.connectAttr('{}.outputRotate'.format(quatToE),'{}.r'.format(outputNode_offset
))
#移動成分の反転接続
cmds.connectAttr('{}.tx'.format(loc),'{}.floatA'.format(mirrorPosNode))
cmds.setAttr('{}.floatB'.format(mirrorPosNode),-1.0)
cmds.setAttr('{}.operation'.format(mirrorPosNode),2)
cmds.connectAttr('{}.outFloat'.format(mirrorPosNode),'{}.tx'.format(outputNode_off set))
cmds.connectAttr('{}.ty'.format(loc),'{}.ty'.format(outputNode_offset))
cmds.connectAttr('{}.tz'.format(loc),'{}.tz'.format(outputNode_offset))
#出力用ノードは、あらかじめ検索しておいた反転対象ノードと位置・向きを合わせておく
cmds.delete(cmds.pointConstraint(mirrorJoint,outputNode))
cmds.delete(cmds.orientConstraint(mirrorJoint,outputNode))
st = cmds.playbackOptions(q = True,min = True)
et = cmds.playbackOptions(q = True,max = True)
cmds.bakeResults(outputOffsetList,sm = True,t = (st,et),at =
('tx','ty','tz','rx','ry','rz'))
ベイクが終わったら反転計算用に作ったノード群は不要になるので、全て削除しておきます。
for node in inputLocList:
if cmds.objExists(node):cmds.delete(node)
for node in culNodeList:
if cmds.objExists(node):cmds.delete(node)
これでアニメーションをグローバル直下のアニメーションとして評価して、ミラーしたアニメーションの挙動として書き出すことができました。ここで出力用のノードと全てのジョイントをコンストレインで接続し、ベイクを行うと......
for j in jointList:
scsJoint = j
if 'Left' in j:
scsJoint = j.replace('Left','Right')
elif 'Right' in j:
scsJoint = j.replace('Right','Left')
if not scsJoint in outputLocDict.keys():continue
cmds.pointConstraint(outputLocDict[scsJoint],j)
cmds.orientConstraint(outputLocDict[scsJoint],j)
#反転アニメーションをベイク
cmds.bakeResults(jointList,sm = True,
t = (st,et),at = ('tx','ty','tz','rx','ry','rz'))
#不要になったoutputノード群は削除
cmds.delete(outputOffsetList)
結果はこちら。
できました! ハラショー!
ちなみにこんな複雑なものも......
ミラーできます!
ハラショォォ!!
Step 06:まとめ
Matrixの概念を理解しておけば、ベクトル計算やQuaternionの計算と組み合わせて複雑な姿勢制御が可能になります。このことはキャラクターリギングのみならず、アニメーション作業においても有効な手段となり得るかと思います。
さて、3回にわたってMatrixを使った事例とTipsを紹介してきました。Matrixには難しい印象を抱いている方が多いと思いますが、ぜひこの機会に少し触れてみていただければ幸いです。 きっとより良い知見になると思いますのでオススメです。
では、今回はこのへんで。
サヨナラ! サヨナラ! サヨナラ!!
Profile.
-

-
山本智人/Tomohito Yamamoto(COYOTE 3DCG STUDIO)
ゲーム開発会社にてグラフィックアーティストとして、モデリング・モーション・エフェクト・UIなどオールラウンドのグラフィック制作を経験後、テクニカルアーティストに転身。現在は株式会社クリーク・アンド・リバー社 COYOTE 3DCG STUDIOにて、社内外問わずアーティストのDCCツールサポートや制作パイプラインの提案・作成・運用を行う。特にアニメーション制御やモーション制作周りのテクニカルサポート・リガーとして様々なプロジェクトに従事