TVアニメ、実写映画、ゲームなどを幅広く手がける株式会社コロビト代表・大島夏雄氏によるCG雑学コラム。一見CGには関係なさそうでも知っていればいつか必ず制作に役立つ、身の回りの様々な知識を紹介していく。
TEXT&ILLUSTRATION_大島夏雄 / Natsuo Oshima(コロビト)
EDIT_小村仁美 / Hitomi Komura(CGWORLD)
<1>「重さの感覚」と「単位」
こんにちは、コロビトの大島夏雄です。今回は「構造力学」に関して書いていきますが、難しい計算式は飛ばして、できるだけイメージをわかりやすくお伝えできればと思っております。記事を書くにあたって改めて勉強したのですが、22年ぶりの数学は忘れていることばかり......。
私は美大を受けたので受験に必要な学科は、国語と英語だけでした。浪人時代に塾で学科の勉強を少しでもすると、実技の先生に「学科なんかやるな!芸大に行くなら必要ない!」と言われていたくらいです。すごく怖い先生でした。話がそれてしまいましたが、構造力学に関して書く前に「単位のはなし」を少しだけ。
CGでも大きさ(サイズ)の感覚はすごく大事です。例えば鉄板で乗り物や建造物をつくっているときに「この厚みは何mm?」「入口の高さは何mだろう?」など、人型のモデルを仮に配置して確認し、鉄板や鎧、布の厚みなども意識しながらモデリングを進めていると思います。
これは、何となく意識する、というレベルではなく、具体的であるべきです。プロジェクトが始まる前には、1グリッド=1mや1グリッド=1cmといったようにスケールを決めますよね。
そこでもう少し具体的にモデリングするときのコツとして、重さの感覚も意識すると、作業を進めやすくなると思います。例えば、1m四方の大きさで厚さ10mmの鉄板の重さはだいたい80kgです。結構重いですよね。戦車の装甲に使われているものは、80mmや180mmもの厚みがあります。厚さ80mmだと1㎡で640kg、180mmだと1㎡で1.5t弱! すごい! こうやって重さの感覚も何となくでも知っていると、より良いものを作れるのではないでしょうか。
物理には様々な単位が出てきます。構造力学を勉強していてよく出てくる単位が力を表す「N(ニュートン)」です。ん?「kg重(kgf)」というのは知っているけど、Nって何だっけ? と思った方は32歳以上かもしれません。実は、平成14年以降、中学の理科で教える力の単位がkg重からNに統一されたのです。私は余裕で「kg重」の方です。
「N」は「国際単位系(SI)」と呼ばれる、国際的に正式採用されている単位のひとつです。こちらに詳しく掲載されていますので興味のある方はぜひ見てみてください。
●産業技術総合研究所 計量標準総合センター
https://www.nmij.jp/library/units/si/
「N」もそうですが、学校で習うことはどんどん変わっていきますね。ちなみに鎌倉幕府設立も今は1192年(いいくにつくろう鎌倉幕府)ではなく、1185年と教えているそうです。
それでは、構造力学に関してはいろいろ書きたいことがあるのですが、今回は基本的なことをいくつか紹介したいと思います。
<2>「力の三要素」と「モーメント」
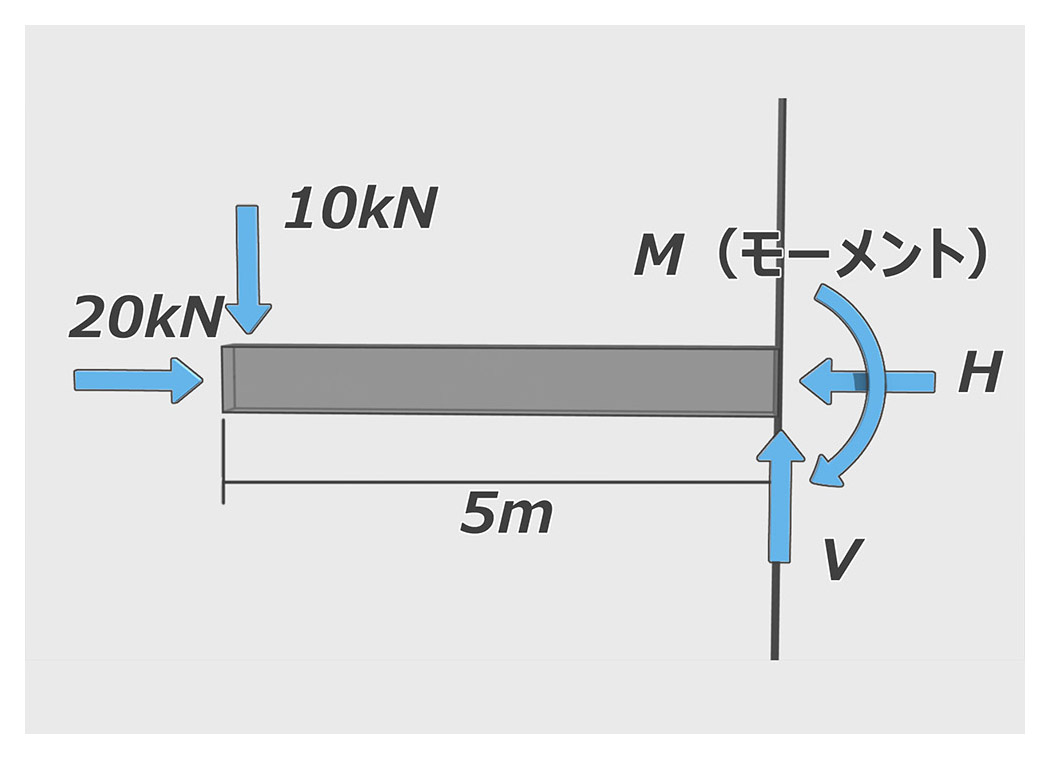
力は「作用点」「方向」「大きさ」の3つの要素で表すことができます。矢印で表現すると便利です。矢印の始点が「作用点」、矢印の向きが「方向」、矢印の長さが「大きさ」となるわけです。
また、物体を回転させようとする力もあります。これを「モーメント」といい、「M」で表します。
上のイラストのような、片側が固定されている5mの梁の先端に10kNの力が加わる場合、根元の反力をそれぞれ求めましょう、という問題があるとします。梁は静止しているので、対となる矢印は同じ力となります。ということは、H=20kN、V=10kNと特に意識しなくてもわかりますよね。そこで問題になってくるのがM(モーメント)、根本は固定されているので回転の負荷がかかるのがイメージできますでしょうか?その力がモーメントです。Mは10kN×5mで50kNmとなります。梁が長ければ長いほど根元にかかる力は大きくなり、より強固に固定する必要があるというわけですね。
<3>内外からの力による変形
薄い金属板に両側から徐々に力を加えると弓なりに変形します。建築物では上からの荷重に対してや、地震などが発生したときの横からの力でこの「座屈」と呼ばれる変形が発生し、その変形が大きくなると崩壊してしまう恐れがあります。
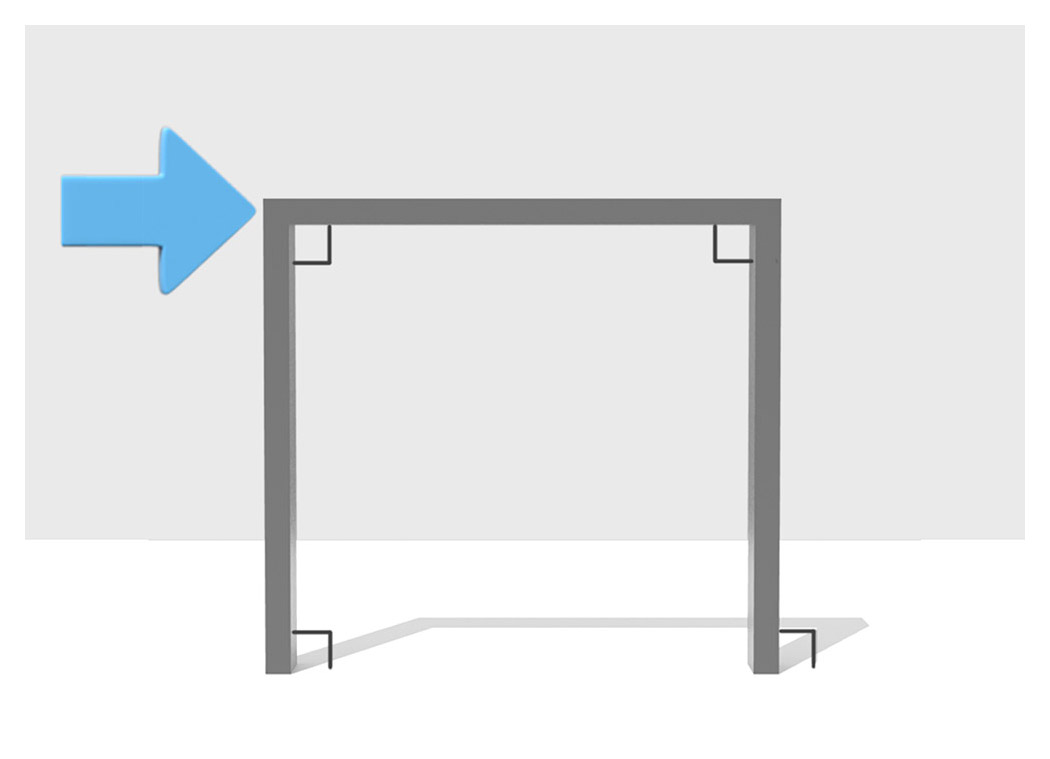
●横からの力による変形この構造物に横から力が加わった場合どのように変形するでしょうか? 部材と地面、柱と天井は直角に固定されています。
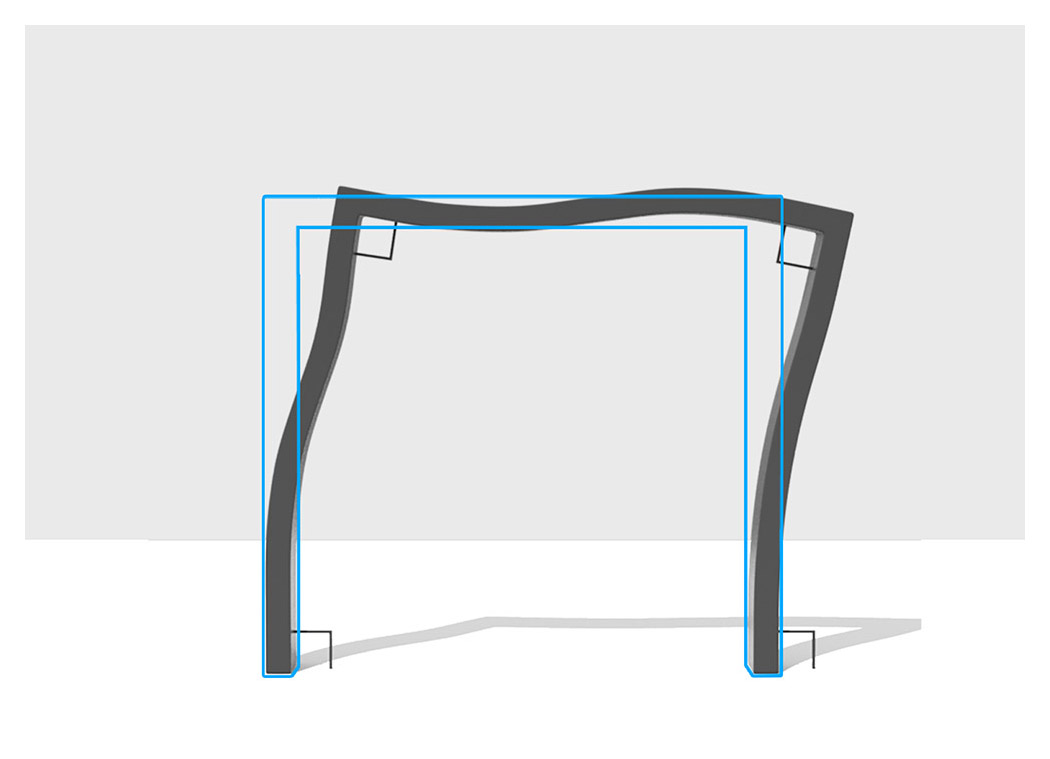
こんな感じに変形します。固定されている箇所はほぼ直角を保ちます。柱と梁の接合も直角を保ちます。柱部分のそれぞれの場所でかかっているモーメントの向きが変わるので山ができます。どのくらいの力でどのように変形するか計算することができるのですが、すごーく大変ですので興味のある方は勉強してみてください!(私も勉強中です......)
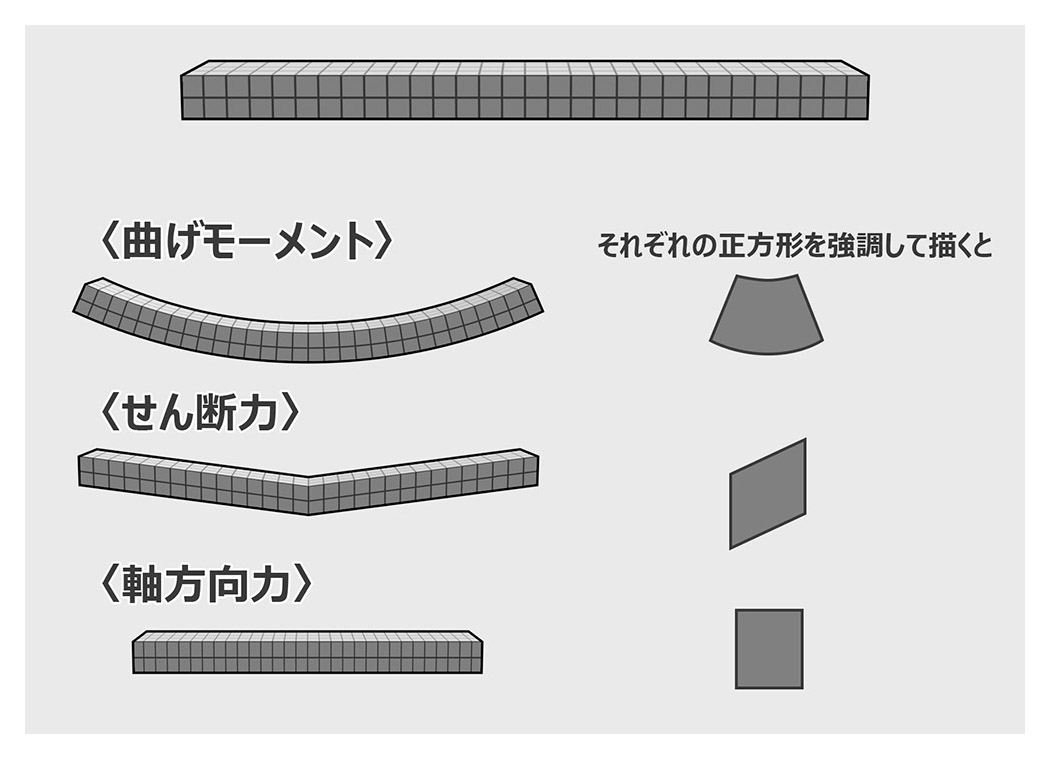
●部材内に生じる力例えば直方体の部材に1cmピッチにグリッドを描き、それに大きい力を加えたときにグリッドの正方形がどのように変形するかを想像するとわかりやすいです。部材自体が変形しようとする力は3種類に分けられます。
・曲げモーメント
正方形は扇田型に変形しています。
・せん断力
正方形は平行四辺形に変形しています。
・軸方向力
正方形は長方形に変形しています。これは伸びたり縮んだりする変形です。
<4>曲がりやすい形、曲がりにくい形
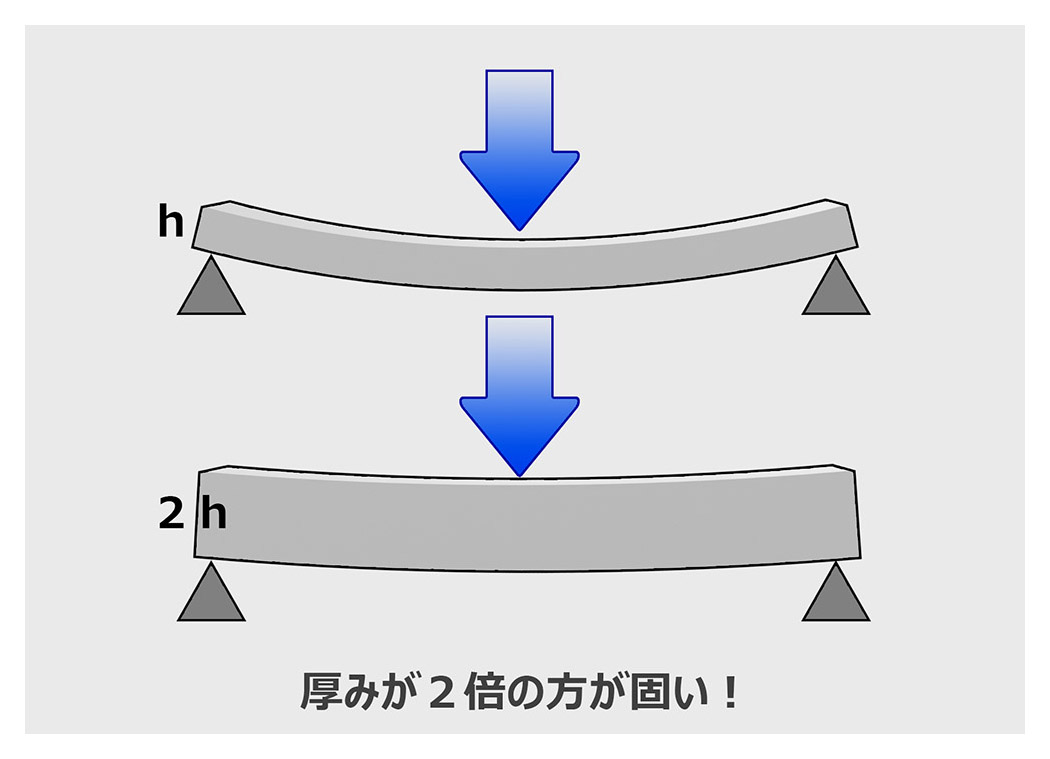
イラストのように部材の厚みが厚くなると強く(たわみにくく)なります。では、どのくらい強くなるのでしょうか?
イメージでは、そりゃ分厚い方が固いよね。と思いますがそこは「構造力学」です。どのくらい固いかを数字で求めたい! そのためには、下記のような手順を踏んで計算していきます。
断面積を求める
↓
断面1次モーメントを求める(さっそく聞いたこともない用語が......)
↓
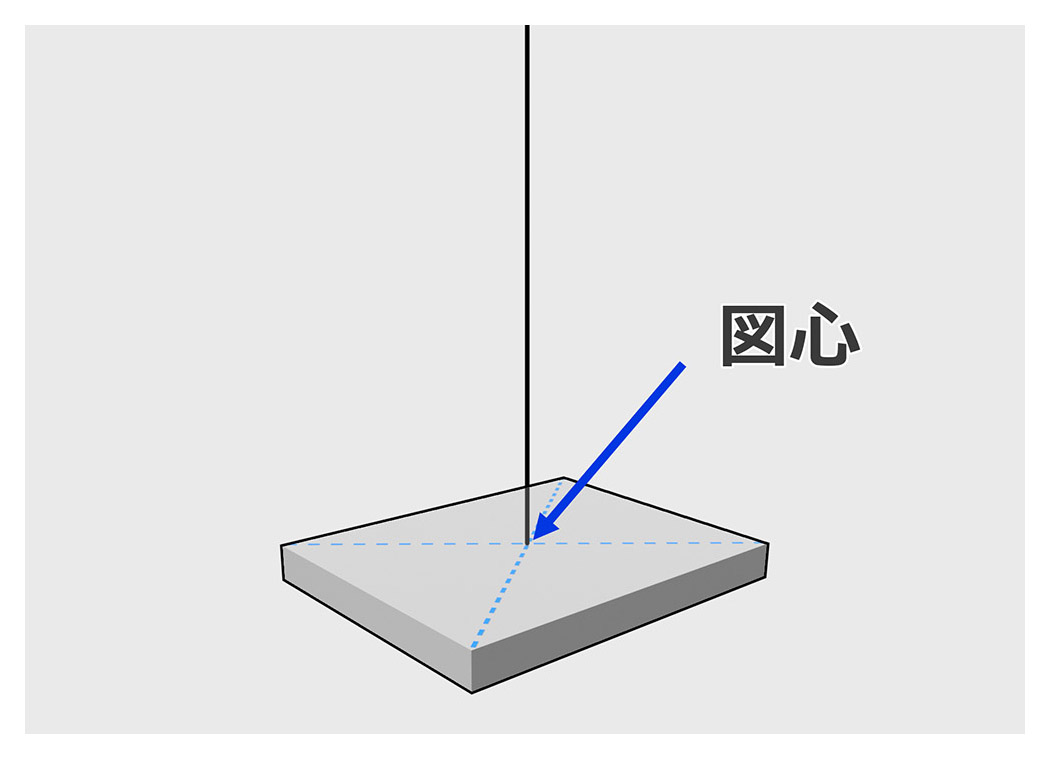
断面積と断面1次モーメントを使って図心を求める(図心:断面に一定の厚みをつけた場合の重心位置のこと)
↓
断面2次モーメントを求める(1次もわからないのに2次がきた!)
↓
断面係数を求める
断面係数が高ければ高いほどたわみにくくなります。この断面係数は頑張れば理解できます。今回は省略しますが機会があれば解説したいと思います。断面係数が計算できるようになると、H鋼とL字鋼の強度の差なども計算して知ることができます。今はネットで簡単に計算してくれるサイトもあります。「断面係数 計算」などのワードで検索してみてください!
●長方形の断面係数長方形の断面係数はこの公式で求められます。数字が大きいほうが強いということです。
例えば厚みだけが異なる部材A、Bがあり、Aは厚みが10mm、Bは厚みが20mmだった場合はBはAの何倍強いでしょうか? 上の公式からhが10と20ということだから、10の2乗は100、20の2乗は400です。ということは厚みが2倍になると強さは4倍になるということですね!
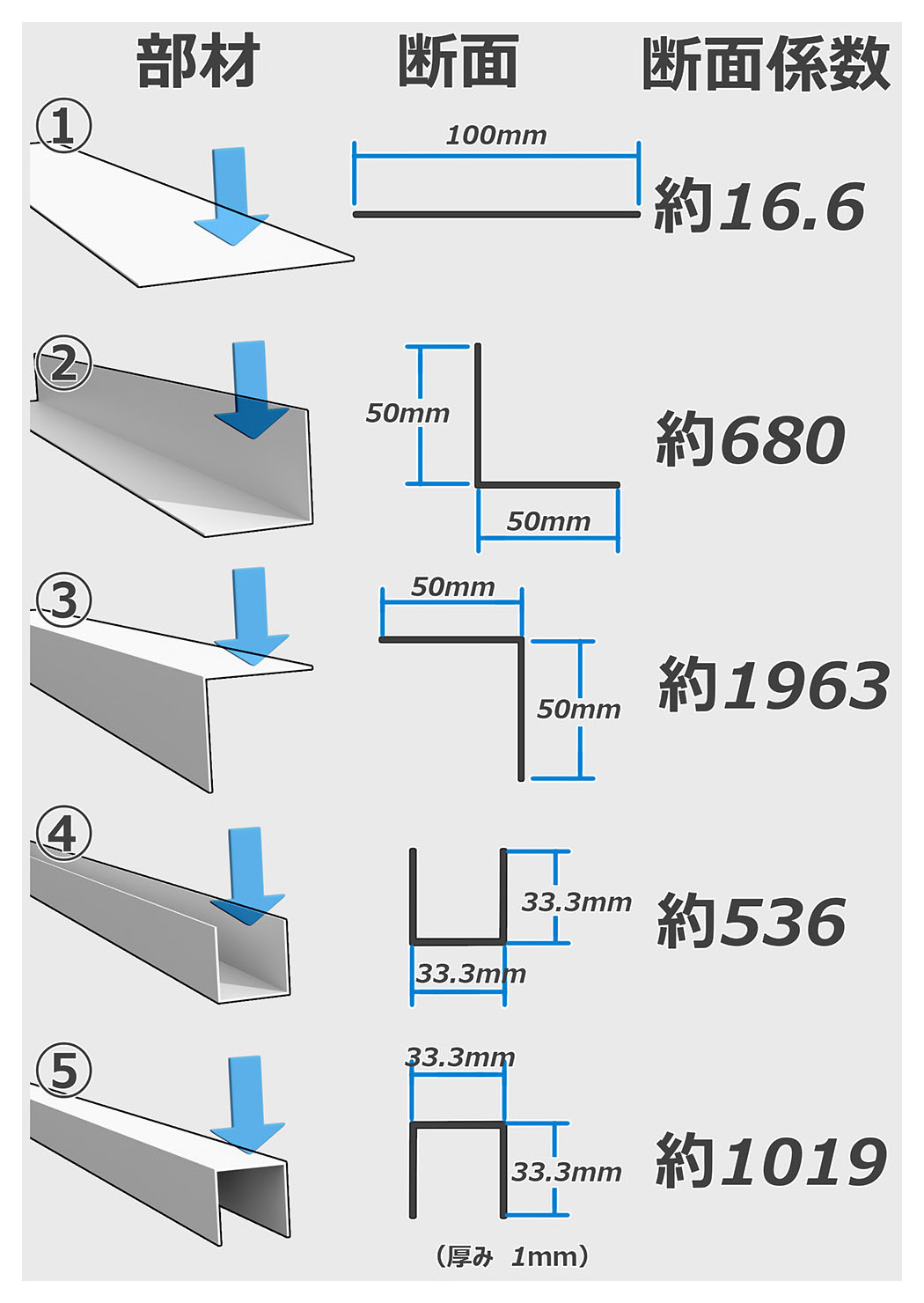
●いろいろな形状の断面係数いろいろな形状の断面係数をいくつかご紹介します。下のモデルは、幅100mm、厚み1mmの部材を曲げてつくることができるものです(実際に曲げると角が丸くなったりしますが、その数値は省いています)。
ほぼ同じ断面積ですが、断面係数はまちまちですね。上から3番目のL字型の逆向きの断面係数が1,963と最も強いという結果になりました。これ以外にこの部材を曲げてもっと強い形状はつくれないかな? と考えてみましたところ、ありました! 板を曲げずに①を90度回転させた形状が一番強いです。断面係数はなんと16,666.66....です!
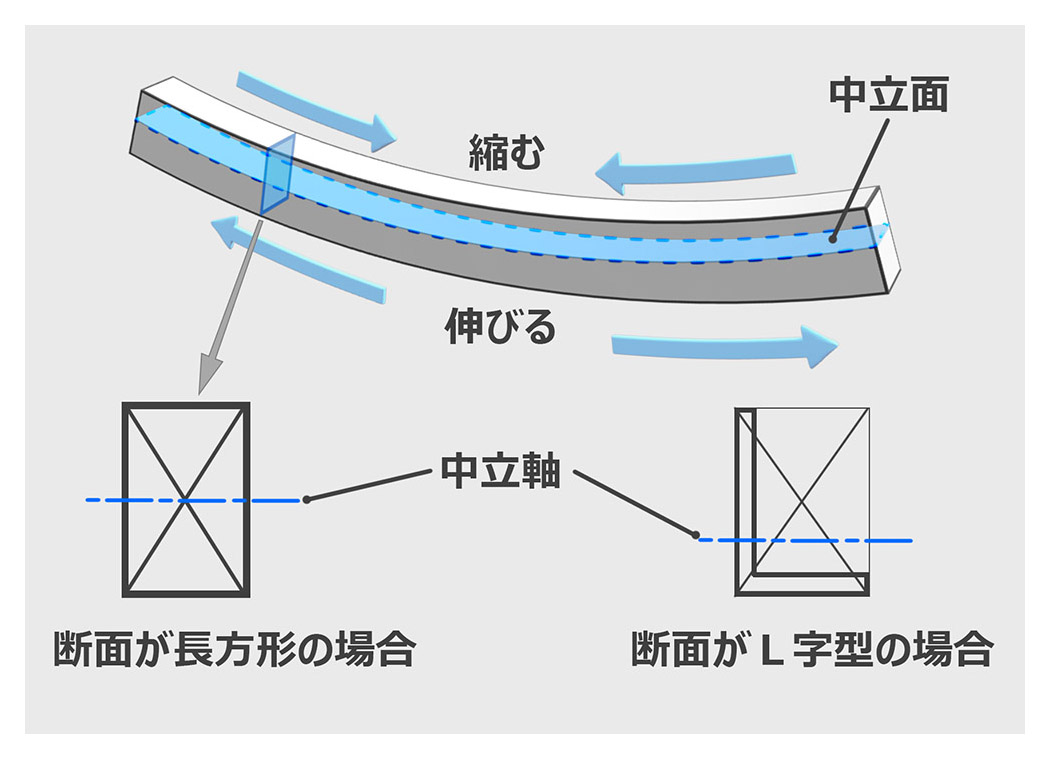
同じ形状の②、③や④、⑤は向きによって強さが大分ちがいますね。曲がる部材を見てみると、下の図の場合上側が縮んで下側が伸びていますね。中間に伸びも縮みもしていない軸があります。これを「中立軸」といい、これは図心と一致します。
L字型やU字型の場合、図心が断面の中心と一致しないため、上下によって強さが変わります。同じ断面積でも強度が変わるということは、同じ鉄の量で強度のある建材をつくることができるということです。そうしてH鋼やL字鋼が生まれました。同じ強度の場合、できるだけ断面積を小さくした方が使用する鉄の量は減ります。鉄が減ると建材の重量は軽くなりますし、値段も安くなります。今の鉄の買取価格は1kg 26円程度です。スクラップの鉄の買取価格ですね。初めに書きましたが10mmの厚みの1m×1mの鉄板が80kgですので、買い取ってもらうと2,080円になります。
<5>おわりに
「構造力学のはなし」はいかがでしたか? モデリングの役に立ちそうでしょうか? 何となくでも力のことをイメージしながらつくると、出来上がるものは大分変わってくるのではないでしょうか。例えば、「90度に固定すると柱や梁が曲がってしまう」ということから橋の橋脚の下に設置されているような「ピン支承」を設置してみても良いでしょう。そうすると、揺れがあっても上面は平行を保つことができます。上部に45度ダンパーを追加しても良いかと思います。このように、デザイン画やイメージボードに描かれていないとしても、いろいろ自分で考え、理由付けすると、説得力があり情報量のあるモデルをつくれるのではないでしょうか。
断面係数に関しては必要以上に大きい建材や分厚い鉄板などは違和感が出てしまいます。強度ギリギリということはないでしょうが、最適な強度に近いモデリングができると良いと思います。そのためには、自分が今つくっているものは何のためのものなのかを理解する必要があります。ディレクターに聞いても明確な答えが返ってこない場合は、自分で決めてしまえば良いのです。この橋は電車が走るのか、人が歩くだけなのか、長さに対して橋脚の数はどのくらいあるのか、など想像しながらモデリングすると進めやすいと思います。現実ではありえない細い建材でモデリングすることで未来感や異世界感を演出したり、現代よりも太くすれば、レトロ感を演出することもできそうです。
構造力学や強度設計は数学の要素が強いので苦手な方もいるかと思いますが、入門書籍も多数発売されていますので、1冊買ってパラパラと読んでみても面白いと思います。私は今回の記事を書くにあたり5冊ぐらい買い、全ページではないですが読みました。結果、とても面白く、興味深く読むことができました。残りの章も時間があるときに読むつもりです。
次回は「空を飛ぶ原理のはなし」に関して書きたいと思っております。空を飛ぶものというと飛行機、ヘリコプター、ロケット、最近ではドローンもあります。それぞれどうして飛ぶことができるのでしょうか? それでは、次回もよろしくお願いいたします。
参考文献
書籍
「改訂版 図説 やさしい構造力学」(浅野清昭・著、学芸出版社)
「建築の構造」(マリオ・サルバドリー、ロバート・ヘラー・共著、望月 重・訳、鹿島出版会)
「直感で理解する! 構造力学の基本」(山浦晋弘・著、学芸出版社)
「建築構造設計・解析入門」(藤井大地、松本慎也・著、丸善出版)
「図解 設計技術者のための有限要素法はじめの一歩」(栗崎 彰・著、講談社)
「加工材料の知識がやさしくわかる本」(西村 仁・著、日本能率協会マネジメントセンター)
Profile.
大島夏雄/Natsuo Oshima(コロビト)株式会社コロビト 代表取締役、リードモデラー
奈良県出身。多摩美術大学(絵画学科 油画専攻)を卒業後、数社のCG制作会社に所属しモデリングチーフを務める。その後、フリーとなり2009年7月2日に株式会社コロビトを設立。ゲーム、映画、アニメ、CMなど様々なジャンルの仕事を手がける
colobito.com