本連載では、アカデミックの世界に属してCG・映像関連の研究に携わる人々の姿をインダストリーの世界に属する人々に紹介していく。第15回では、CGにおける数値計算方法を専門とし、特に、光の伝搬シミュレーションに基づく写実的な画像のレンダリングについて研究する東京大学大学院の蜂須賀恵也准教授に自身の研究室について語っていただいた。なお、本記事の内容は執筆当時(2019年10月)のもので、2021年2月現在、蜂須賀氏はカナダ オンタリオ州のウォータールー大学に在籍している。近況はこちらを参照いただきたい。
※本記事は
『CGWORLD + digital video』vol. 255(2019年11月号)掲載の「ACADEMIC meets INDUSTRY 東京大学大学院 情報理工学系研究科 蜂須賀研究室」を再編集したものです。
TEXT_蜂須賀恵也 / Toshiya Hachisuka(ウォータールー大学・2021年2月現在)
EDIT_尾形美幸 / Miyuki Ogata(CGWORLD)
転載にあたり、近況のご報告
本記事の月刊誌掲載後、2020年の9月にカナダのウォータールー大学にAssociate Professorとして異動しました。研究テーマや研究室のポリシーは変わらないものの、私自身が学生として経験したような研究環境や学生生活が、自分の学生にもより提供しやすくなったと思っています。ウォータールー大学は日本ではあまり馴染みがない学生も多いかもしれませんが、コンピューターサイエンスの分野では、世界的にトップランクの教育・研究を行なっている大学です。また、産業界との結び付きも強く、アメリカのシリコンバレーをはじめとして、多くの著名なIT企業で卒業生が活躍しています。日本の学生の皆様は留学先の候補として、企業の皆様は採用・共同研究先の候補として、ぜひ検討してみてはいかがでしょうか。
-

-
蜂須賀恵也
[執筆当時(2019年10月)]
東京大学大学院 情報理工学系研究科 准教授
[2021年2月現在]
Associate Professor
David R. Cheriton School of Computer Science, University of Waterloo
Ph.D.(コンピュータサイエンス)
専門分野:CG、レンダリング、数値計算、統計計算
cs.uwaterloo.ca/~thachisu/
学部卒業後、米国でPh.D.を取得
東京大学の蜂須賀恵也です。私は2006年に東京大学の工学部を卒業した後、米国のカリフォルニア大学サンディエゴ校(UCSD)に入学し、2011年にPh.D.を取得しました。日本では、私のように学部卒業後、すぐに留学するケースは珍しいと思います。私の場合、学部学生のときからCGに興味があり、様々な論文を読んでいく中で、活躍している研究者の名前を知る機会がありました。そして、研究をするなら世界的に活躍している研究者の下で行うべきだと考え、その手段として留学という選択肢が自然と視野にありました。明確な目的をもって留学したことで、結果として大変充実した学生生活になったと思っています。これから進学を考えている皆さんにも、ぜひ、同じような経験をしてほしいと思います。
UCSDでPh.D.を取得した後の進路として、企業の研究所や大学の教員など、様々な選択肢を考えました。結果として、やはり研究と教育に関わりたいという考えから、デンマークのオーフス大学でAssistant Professorとして、CGの研究グループを起ち上げることになりました。オーフス大学での教員としての生活は大変充実しており、デンマーク滞在中、日本に帰国することはまったく考えていませんでしたが、縁あって2014年に東京大学に戻ることになりました。そして、現在(2019年10月当時)、東京大学大学院 情報理工学系研究科の創造情報学専攻で、准教授として研究室を主催しています。私の専門はCGにおける数値計算方法で、特に、光の伝搬シミュレーションに基づく、写実的な画像のレンダリングについて研究しています。
東京大学へ戻った後、国際色豊かな研究室を開設
私が所属する創造情報学専攻は、情報理工学系研究科のほかの専攻から、複数の教員が異動して成り立っています。伝統的なコンピュータサイエンスの専攻とはちがい、コンピュータサイエンスとほかの分野にまたがるような研究を推進する、非常にユニークな専攻です。毎週行われる創造情報学輪講では、自分の研究分野に限らず、コンピュータサイエンスに関連する様々な分野で、各学生が行う最新の研究内容について知ることができます。本専攻は特定の学部をもたず、留学生や東京大学以外から進学する人も多くいます。
私の研究室は、文京区の弥生キャンパスのI-REF棟という建物の中にあります。I-REF棟は2013年に建築学専攻の協力でリノベーション工事がなされており、キャンパス内でも特に新しい綺麗な環境で研究に取り組めます。学生には、ほかの研究室と混合で、各フロアにデスクスペースが割り当てられており、日常的に研究室間の垣根が低い環境で学ぶことができます。
▲本研究室があるI-REF棟は6階建ての建物で、3〜5階は各教員の部屋以外はオープンスペースになっており、6つの研究室の学生が混合で日々研究に取り組んでいます
本研究室は、2014年の夏、私の日本への帰国と共に開設されました。オーフス大学で指導していた学生はほぼ修了していたこともあり、開設当初は私ひとりでスタートしました。比較的新しい研究室と言えますが、当初の人数からかなり増えており、本記事の執筆時点では、ポスドク2名、博士3名、修士14名、研究生1名という体制で、CGと数値計算の組み合わせについて日々研究しています。
本研究室メンバーの半数以上は外国出身で、非常に国際色豊かな研究室であり、研究室ミーティングでは英語による議論が中心となることもよくあります。また、創造情報学専攻は女性の学生が少ない傾向にあるのですが、本研究室はほかの研究室に比べて女性の割合が高く、男女比率、内部・外部からの進学比率、国内・国外の出身比率など、様々な面でメンバーのバランスがとれている研究室です。一般的には、コンピュータサイエンスでは男女比率の偏りが問題視されていますが、CGを専門に活躍している女性研究者は多いので、本研究室からもそのようなロールモデルとなる女性研究者が輩出できればと思っています。
レンダリングをより数学的なアプローチから研究
冒頭で述べた通り、私の専門はレンダリングです。特に、コンピュータ上で光の伝搬をシミュレーションし、その結果を用いて写実的な画像を生成する方法について、数学的側面から研究しています。このようなシミュレーションは、最近の映画やゲームなどで、実写と見分けがつかない画像をつくるための基盤となる技術であり、CGの研究分野の中でも歴史が古いものです。歴史が古いということは、それだけ多くの研究が行われているということでもあり、レンダリングでは新しい発見が難しいと考える研究者も多くいます。
しかし、私は個人的にはこの意見に賛同しておらず、レンダリングをより数学的なアプローチから研究することで、綺麗な画像をつくるという目的の達成だけでなく、非常に多くの知見が得られると考えています。しがたって、私の研究アプローチは、与えられた問題を解く方法を提案するだけでなく、今までにない定式化や方法を提案する数学的アプローチが多く、応用数学の研究とも捉えることができます。詳しくは後述しますが、レンダリングに限らず、ほかの問題にも適用可能な研究成果も多く、レンダリングの研究には分野を超えた大きな可能性があると考えています。
VPLを基にした、効率的な照明計算
▲本研究では、グラフィックスハードウェアを効率的に使った照明計算の方法を提案しています。高速な計算が可能な一方で、計算結果の精度が悪いVPLという方法を基にして、その計算時間を増やすことなく、精度を上げることに成功しました。【左】従来の方法(VPL、Clamped VPL)では、局所的に明るくなる誤差や、全体として暗くなる誤差がありますが、【右】提案手法では、長時間かけて計算した正しい結果に近い画像が得られています。本研究の詳細は、こちらをご覧ください
次ページ:
研究成果は、国際学会で論文として発表することを推奨
研究成果は、国際学会で論文として発表することを推奨
本研究室では、必ずしも全ての学生がレンダリングについて研究しているわけではありませんが、問題に対して数学的かつ本質的に新しいアプローチを試みるという点では共通しています。研究成果は国際学会で論文として発表することを目標としており、CGの分野で最も有名なSIGGRAPH、SIGGRAPH Asia、Transaction on Graphicsをはじめ、毎年数本の論文を発表しています。一方で、学会でのデモの展示や、国内学会への投稿などはあまり行なっていませんし、学生にもなるべく国際学会で発表するように指導しています。極端な方針のように見えますが、このような考えにいたったのには理由があります。
まず、CGの研究成果の発表方法は、デモやアート作品といったかたちが選択されることもありますが、私はあくまでもCGの研究としての学術的価値を追求したいと考えており、学術論文の発表を重視しています。CGに限らず、コンピュータサイエンスは研究と実用が近い関係性にあり、民間企業でも盛んに研究開発が行われています。そのような中で、大学で行う研究の存在意義は、民間企業では応用に直結しないなどの理由で追究されないことの多い、純粋な学術的興味による基礎研究への貢献だと考えます。
また、インターネットの普及により、情報は世界中にすぐに伝わるようになりました。そのため、世界中の研究者に伝わるように研究を発表することが重要であると考えており、日本語だけによる発信は、より多くの人に知ってもらえる機会を逃していると言えます。
このような理由から、私の研究室では、学生に国際学会や英語論文での発表を推奨しています。私のWebサイトでは、前述のような研究成果の発表や、大学院進学、研究室についての私の考え方をまとめた資料を公開しており、私の研究室の学生だけでなく、大学院進学を考えている学生が広く参考にしているようです。
学術的興味から始めた研究でも最終的には企業で直接役に立つ
本研究室では、民間企業との共同研究も多数行なっています。これまでの共同研究先は、Samsung、Disney、ニコン、デジタル・フロンティア、トライエース、Autodesk、Facebookなどで、それぞれの企業の研究者と共同し、研究を行なってきました。研究は、学術的興味から始めることが多いですが、それでも、最終的に企業で直接役に立つような成果が得られることがあります。例えば、直接の共同研究ではありませんが、これまでの研究成果は、レンダラのRenderManなどをはじめ、映像産業で使われています[1]。特定の応用を起点としないがために、多くの問題に適用可能な成果が得られることも多く、結果として様々な応用ができ、幅広い用途で役に立つというのが、基礎研究の魅力だと考えています。
シャボン膜の動きのシミュレーション
▲本研究はレンダリングの研究ではありませんが、微分幾何学のGeometric flowという考えと、シャボン膜の動きを初めて結びつけたもので、本研究室のCGに対する数学的アプローチを表す研究のひとつです。本研究の詳細は、こちらをご覧ください
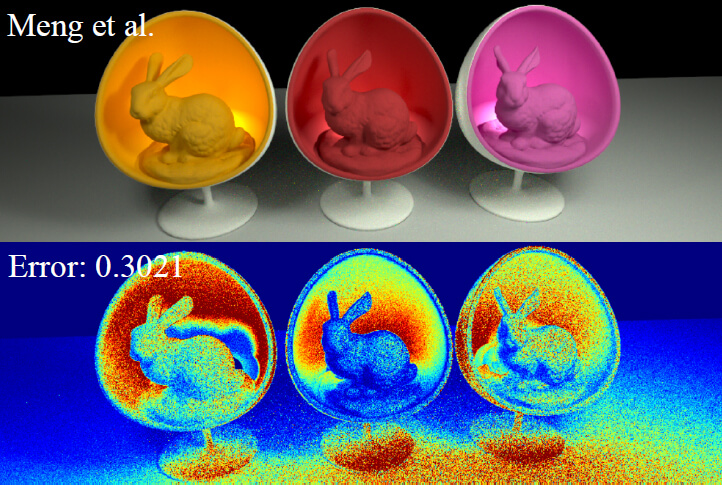
分光反射率の再現
▲本研究では、三原色の反射率から分光反射率(光の波長ごとの反射率)を再現しました。【上】【中】従来の方法(Smits、Meng et al.)では実在する材質の分光反射率を再現できず、結果として微妙な色の誤差が出ますが、【下】提案手法では、三原色と測定された分光反射率との間の数学的関係を初めて導き出し、その再現に成功しました。本研究の詳細は、こちらをご覧ください
分野を超えた知識の融合がCGの研究の魅力
卒業生の進路は、ゲーム会社や企業の研究所、海外の大学の研究員などがあります。明確にやりたいことが決まっている人が多いため、自ずとCGに関わる就職先を選ぶ人が多いように思います。前述したように国際色豊かな研究室ということもあり、国内での就職にこだわらない学生も多くいます。また、インターンシップなども推奨しており、共同研究先の企業や海外大学にインターンシップに行くケースも多くあります。インターンシップと言っても、日本で主流の数日から1週間の体験型のものではなく、数ヶ月の期間で、かつ実務に関わり、給与も出るようなものを考えており、そのようなかたちでのインターンシップを、企業と共同で設定してもらうこともあります。
CGの研究の魅力はいろいろありますが、特に、分野を超えた知識の融合が魅力的だと考えています。例えば、後述する研究は、一見すると関係ない統計計算とレンダリングを結びつけるもので、どちらかの分野に留まるだけでは生まれなかった成果だと思います。ほかの分野の研究者のもつ知見が、CGの画期的な成果に結びつくことは珍しくありませんし、CGの分野でよく知られた手法が、ほかの分野でも有効なケースも多くあると考えています。ある意味で、誰でも自分の強みを活かしてCGの研究に関われるとも言えると思いますので、そういった研究に興味のある学生や企業の方には、ぜひ研究室訪問などを通して魅力を知ってもらえればと思います。
次ページ:
Progressive Photon Mapping
RESEARCH 1:Progressive Photon Mapping
・研究背景
写実的な画像をコンピュータ上で生成する最も自然な方法として、現実世界での光の伝搬の様子をコンピュータ上でシミュレーションし、カメラや目に届く光の強さを計算する方法があります。これを行うには、ライトや太陽などの光源から出た光が、物体に当たって反射・散乱・屈折し、最終的にカメラや目に届くまでに、光の強さがどのように変わるかを計算する必要があります。この計算の難しさのひとつは、光源から出た光がカメラや目に届くまでの光の経路には、反射・散乱・屈折の回数や、それらが起こる位置などによって、ありとあらゆる可能性があるため、それらをできる限り網羅する必要があるという点です。本研究では、従来のいずれの方法でも、ある特定の(しかし日常的に起こる)経路のパターンを網羅することができないという問題に注目し、それらを世界で初めて扱える光伝搬シミュレーションの方法を開発しました。
・主な先行研究
光伝搬シミュレーションで最もよく使われる方法として、モンテカルロ積分という数値計算の方法があります。これは、全ての光の経路を網羅するという問題を、積分の問題として定式化しなおし、その積分を数値計算によってコンピュータ上で解くアプローチです。モンテカルロ積分は、光の経路をランダムに生成し、それを何度もくり返して多数のランダムな経路をまとめることで、近似的に全ての光の経路を網羅するというアイデアに基づいています。計算時間を増やせば、それだけたくさんの経路を考慮することが可能になり、計算時間に応じてより正確な結果が得られる特徴があります。この方法は近年の映画などでも盛んに使われており、様々なケースで効果を発揮します。しかし、ガラスや金属の反射、レンズによる屈折と、LEDや電球などの照明が同時に存在すると、モンテカルロ積分におけるランダムな経路の生成では、たとえ無限に計算したとしても、全ての光の経路を網羅できないことが知られていました。前述の要素を含む画像を生成しようとすると、異常に暗い画像が生成されるなどの問題が起きます。これは本質的に解決できない問題だと考えられていて、実用の際にはそのような問題が起こらないようアーティストが調整をくり返すか、もしくは問題があることに気づかない場合もありました。
・研究内容、研究方法
本研究では、モンテカルロ積分ではなく、別の方法として存在していた密度推定法に注目しました。この方法では、光の経路の密度を計算すると、それがそのまま光の強さになるという事実に基づいて光伝搬シミュレーションを行います。密度推定法は、金属の反射やレンズによる屈折などがあっても、全ての光の経路を網羅できるという特徴があります。しかし、密度推定法で正確な計算をするためには、理論的に無限の計算量とメモリ消費量が必要なことが知られており、正確な計算をするための方法としては捉えられていませんでした。・研究の新規性
本研究では、密度推定法の根本的な問題を解決する、新たな密度推定法の枠組みである「漸進密度推定法」を開発しました。漸進密度推定法は、正確な計算が必要な場合でも、メモリ消費量を一定に保てる新たな理論を提案しており、モンテカルロ積分と同様に、計算時間を増やすだけで、より正しい計算結果が得られます。漸進密度推定法によって、ガラスや金属の反射、レンズによる屈折と、LEDや電球などの照明が同時に存在するようなケースにおいて、世界で初めて、全ての光の経路を網羅した正確な光伝搬シミュレーションを行うことが可能になりました。提案した方法は、Progressive Photon Mapping[1][2]と呼ばれ、そこから派生した方法も含めると、500件以上の論文からの引用があり、光伝搬シミュレーションの新たな枠組みとしての研究が進んでいます。本記事の執筆時点でも、全ての光の経路を安定して扱える唯一の方法であり、結果の妥当性を検証するための参考となる計算方法として使われています。ところで、密度推定法は、CG特有の方法ではなく、統計計算の分野で長い歴史があります。しかしながら、メモリ消費量の問題にはあまり注目されておらず、漸進密度推定法は、統計計算の方法としても新しいものと言えます。したがって、単に光伝搬シミュレーションでの応用に限らず、密度推定法が必要な多くの問題に適用可能であると考えています。
▲Progressive Photon Mappingとそれまでの光伝搬シミュレーションの手法の比較。ガラスのランプの中に光源があり、それが部屋全体を照らしているシーンのレンダリングを行なった結果です。【上】の3つはモンテカルロ積分に基づく手法で、ガラスのランプを通過するはずの光が極端に暗いことがわかります。【左下】は従来の密度推定法を使った計算で、ガラスのランプを通る光も含めて、全体的に上手くいっているように見えますが、拡大画像を見ると、詳細がぼけてしまっているのがわかります。【右下】はProgressive Photon Mappingの計算結果で、モンテカルロ積分と同じ計算時間で、メモリ消費量の限界に影響されることなく、精度の良い計算結果が得られていることがわかります
▲3個の時計がデスクランプによって照らされており、カメラによるボケが発生しているシーンを、同じ時間で計算しています。モンテカルロ積分を用いた【左】は、全体的に上手く計算できていません。Progressive Photon Mappingを用いた【中】は、照明は上手く計算できていますが、ボケの計算の精度は十分ではありません。Progressive Photon Mappingを拡張した、Stochastic Progressive Photon Mappingを用いた【右】は、複雑な照明とボケの組み合わせを上手く計算しています
・制作現場での実用と、今後の課題
Progressive Photon Mappingは光の経路を全て扱えるため、照明の正しい計算が必要な場面や、ガラスや金属による反射・屈折によって生まれる複雑かつ綺麗な光のパターン(コースティクス)を計算する場合に、ほぼ必須となる技術です。例えば、テーブルの上のコップが、電球からの光に照らされている、というだけで、Progressive Photon Mapping以外の方法では、正しい画像は計算できません。世界中の映像制作現場で使われているRenderManにも、Progressive Photon Mappingとモンテカルロ積分を統一した後続の方法であるVertex Connection and Merging / Unified Path Sampling(これもわれわれの研究成果のひとつです[3])が実装されています。
モンテカルロ積分に比べて大きなメリットがある漸進密度推定法ですが、デメリットのひとつとして、モンテカルロ積分だけで簡単に計算できるケースでは、漸進密度推定法の方が、やや計算効率が悪いという問題があります。前述のVertex Connection and Merging / Unified Path Samplingでは、モンテカルロ積分と漸進密度推定法の自動的な使い分けに成功していますが、それでもまだ個別の方法だけで簡単に計算できる場合には計算効率が下がるため、それを解決することが大きな課題のひとつです。
▲Unified Path Samplingでは、【左】モンテカルロ積分と、【中】密度推定のそれぞれにおいて、最も効率的に計算できる光の経路を自動的に特定し、それらを組み合わせて【右】最終的な画像を計算することができます。この方法は、数学的には、モンテカルロ積分と密度推定をひとつの定式化によって表すことで達成されます
・参考文献
[1]Toshiya Hachisuka, Shinji Ogaki, Henrik Wann Jensen, "Progressive Photon Mapping", ACM Transactions on Graphics(SIGGRAPH Asia 2008)
[2]Toshiya Hachisuka, Henrik Wann Jensen, "Stochastic Progressive Photon Mapping", ACM Transactions on Graphics(SIGGRAPH Asia 2009)
[3]Toshiya Hachisuka, Jacopo Pantaleoni, Henrik Wann Jensen, "A Path Space Extension for Robust Light Transport Simulation", ACM Transactions on Graphics(SIGGRAPH Asia 2012)
次ページ:
Progressive Photon Mapping
RESEARCH 2:マルコフ連鎖モンテカルロ法
・研究背景
前述したように、光の伝搬シミュレーションでは、光源から出てカメラや目に届く、全ての光の経路を計算します。もちろん、そのような光の経路は実際には無限に存在するため、コンピュータ上でシミュレーションする際には、限られた計算時間の中で、なるべく多くの光の経路を扱うことが重要になります。モンテカルロ積分であっても密度推定法であっても、通常、そのような経路はランダムに生成されます。計算時間が無限にあれば、ランダムに生成したとしても、いずれは全ての経路を網羅するだろうと期待できます。しかしながら、実際には計算時間は有限のため、ランダムに生成するのは実はあまり効率が良い方法とは言えません。例えば、小さな窓から光が入り込んでいるような部屋の中の画像を計算したいとします。ランダムに経路を生成すると、ほとんどの場合、窓を通過する経路は生成されず、画像の計算に直接関係のない経路が大量に生成されることになり、計算時間が大幅に無駄になります。本研究では、そのようなケースにおいて計算に有効な経路を自動的に生成するため、マルコフ連鎖モンテカルロ法を用いた光伝搬シミュレーションについて研究しました。
・主な先行研究
光の経路をランダムに生成する方法は、モンテカルロ法とも呼ばれ、現在の光伝搬シミュレーションで主流となっている方法です。しかしながら、前述のように、ランダムに生成された光の経路は、画像の計算に常に有効とは限りません。これを解決する方法のひとつとして、例えば、光が通過する可能性が高い窓がどこにあるかなどをアーティストが指定する、「ポータル」と呼ばれる方法がありますが、シーンごとに手作業での指定が必要であり、アニメーションなどの制作時には非効率的です。そこで、光の経路が実際に画像にどれくらい寄与するかを自動的に考慮し、寄与する光の経路だけを集中して生成する様々な方法が研究されており、その中のひとつとして、マルコフ連鎖モンテカルロ法があります。
・研究内容、研究方法
マルコフ連鎖モンテカルロ法では、モンテカルロ法とちがい、光の経路を逐次的に生成します。例えば、窓を通過するような、とある光の経路がわかっていたとします。モンテカルロ法では、この情報は無視され、次に生成する経路は完全にランダムです。一方で、マルコフ連鎖モンテカルロ法は、この窓を通過することがわかっている光の経路を「少しだけ」変更することで、次の新たな光の経路を計算します。窓を通過する経路から「少しだけ」しか変更がないので、そのような新たな光の経路も、再び窓を通過する可能性が高いと考えられます。これを何度もくり返すことで、窓を通過する経路を集中的に生成することができます。ここで難しい点は、「少しだけ」変更した経路が、また有効な経路となるように上手く変更方法を設計することです。本研究では、その点に注目しています。
▲モンテカルロ法【上段】とマルコフ連鎖モンテカルロ法【下段】の比較。太陽光が外から入ってくる部屋をレンダリングする場合、モンテカルロ法では、生成されたほとんどの経路は部屋の外側に位置することになり、画像の計算誤差として見えることになります。マルコフ連鎖モンテカルロ法を使うと、同じ計算時間であっても、画像の計算に有効な、部屋の中に入る光の経路を集中的に生成することができるようになり、それぞれの計算時間でモンテカルロ法よりも正確な結果が得られます
▲照明の詳細なパターンにズームする場合も、マルコフ連鎖モンテカルロ法を使うと、モンテカルロ法よりも正確な結果が得られます
・研究の新規性
本研究室では、このテーマに関するいくつかの研究成果があります。本記事では、そのうちのひとつについて紹介します。マルコフ連鎖モンテカルロ法で、すでにわかっている経路を「少しだけ」変更する方法として、経路を生成するための関数に与える引数の値を変更する方法と、光の経路を直接変更する方法との、2つが研究されてきました。これまで、その2つの方法は完全に別の方法だと考えられており、マルコフ連鎖モンテカルロ法を使う場合は、どちらかを選んで計算を実行する必要がありました。ところが、それぞれの方法で効率良く計算できるケースがちがうことが知られており、使い分けが非常に難しいという問題がありました。
そこで、2つの方法の間を数学的に結びつける枠組みを考案し、2つの方法を自由に組み合わせた計算を可能にする方法を開発しました[1]。これにより、従来別のものと考えられていた2つの方法の関連がクリアになり、マルコフ連鎖モンテカルロ法における従来の研究の多くをひとつの枠組みに統合することができました。
▲光の経路を生成する関数の引数を変更する方法【左】では、金属の反射による光の経路を効率的に捉えることができる一方で、ざらざらした材質に到達する光の経路は効率良く計算できません。対照的に、光の経路を直接変更する方法【中】では、ざらざらした材質に到達する光の経路を効率良く計算できる一方で、金属の反射による光の経路は効率良く計算できません。これまで2つの方法は別々のものと考えられてきましたが、本研究【右】ではそれらを初めて数学的に統一し、両方のケースで効率の良い計算ができるようにしました
・制作現場での実用の可能性
マルコフ連鎖モンテカルロ法は、ランダムに経路を生成すると計算時間が無駄になるケースにおいて、自動的かつ効率的な経路生成を可能とします。現在のところ、映像制作の現場では従来のモンテカルロ法が主流であり、例えば窓から入る光の経路を生成するケースでは、光が入る窓の位置を手作業で指定するか、計算効率が悪いことを承知の上で指定する作業を省いて計算するか、といった選択肢に限定されてしまうことが多いようです。この問題を根本的に解決する可能性がある、おそらく現時点で唯一の方法がマルコフ連鎖モンテカルロ法です。後述する問題が解決すれば、映像制作の現場での普及が進み、多くの実用的なケースで計算効率の大幅な向上が期待できます。
・今後の課題
マルコフ連鎖モンテカルロ法では、経路を少し変更して次のものを生成する、という方法の性質上、生成された経路同士が似通ったものになることがあります。十分に計算時間があれば、全体として、十分にちがった経路が生成されることは理論的に保証されていますが、実用上は、限られた計算時間の中で、なるべくちがう経路を多く生成することが重要です。この問題は、例えば限られた計算時間では、たくさんある窓の中のひとつしか経路が生成されないといった問題につながり、マルコフ連鎖モンテカルロ法の実用化に際しての、重要な課題となっています。
・参考文献
[1]Hisanori Otsu, Anton S. Kaplanyan, Johannes Hanika, Carsten Dachsbacher, Toshiya Hachisuka, "Fusing State Spaces for Markov Chain Monte Carlo Rendering", ACM Transactions on Graphics(SIGGRAPH Asia 2018)
info.
-

-
月刊CGWORLD + digital video vol.255(2019年11月号)
第1特集:僕たちがBlenderを使う理由
第2特集:アニメCG×ゲームエンジン
定価:1,540円(税込)
判型:A4ワイド
総ページ数:128
発売日:2019年10月10日
cgworld.jp/magazine/cgw255.html