TVアニメ、実写映画、ゲームなどを幅広く手がける株式会社コロビト代表・大島夏雄氏によるCG雑学コラム。第4回は「黄金比」「白銀比」のちがいや実際に使用されているもの、それぞれの特徴などについて紹介する。
TEXT&ILLUSTRATION_大島夏雄 / Natsuo Oshima(コロビト)
EDIT_小村仁美 / Hitomi Komura(CGWORLD)
<1>"美しさ"のヒントとしての黄金比・白銀比
もう年が明けてから大分経っておりますが、2019年1回目の連載ということで、明けましておめでとうございます。コロビトの大島夏雄です。筆者は2018年の初めに2つの目標を決めました。ひとつは「海外に行く」。実は筆者は海外に行ったことがありません。もうひとつは「自主制作をどこかで発表する」。この2つを目標に掲げていましたが、結局両方とも未達成で終わってしまいました。ということで、2019年もひき続きこの2つを目標にしようと思います。ここに書いてしまったので、少なくともどちらかは達成したいです。それでは、「黄金比・白銀比のはなし」、いってみましょう!
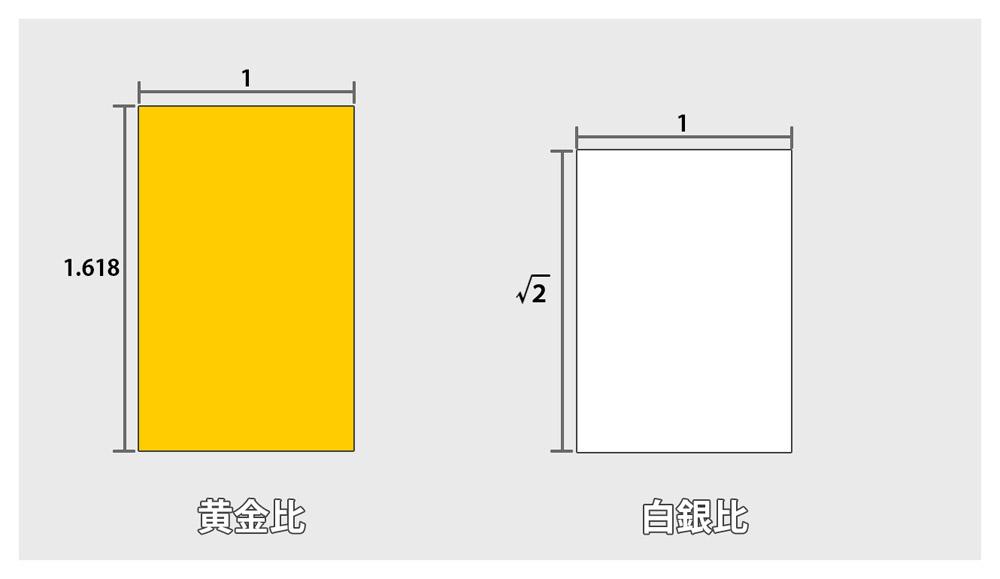
ご存知の方も多いと思いますが、「黄金比」「白銀比」とは、人間が無意識に美しいと感じる比率のことを言います。
図の左側が黄金比で、対比は1:1.618...です。右側は白銀比で、対比は1:√2です。√2は1.41421356237...ヒトヨヒトヨニヒトミゴロ...と覚えましたよね。2つを比べてみると、黄金比の方がスラっとしています。図面やデザイン画がない状態から何かをモデリングするとき、この「黄金比」や「白銀比」を意識すると、センスの良いシルエットがつくりやすいと思います。
この連載ではよく「○○するとつくりやすい」という言い方をしていますが、例えば何も考えずにモデリングする場合を考えてみましょう。何も考えず、適当に縦横比を決めてモデリングすると、ヒントやとっかかりがなくてもつくりづらいとも思わず、どんどん作業を進めていくことができるでしょう。でも、納得のいくモデルを仕上げるまでには時間がかかってしまうかもしれません。
本来何かをつくるときにはそれ相応の理由があり、その理由を基にサイズを決めてつくるものです。それはどこで使うものなのか。家で使うのか、電車などの移動中にも使うのか。家なら家族の人数や、ドア・窓といった既製品のサイズ、水回りの配置、土地の面積、建築法などからサイズを決めます。適当につくっているものなどないでしょうし、あったとしてもそれは使い勝手の悪い無価値なものになってしまう可能性が高いです。
CGで何かをモデリングするときには、生活背景や材料費といったことはそれほど考える必要はないかもしれませんが、やはりつくるためのとっかかりは必要です。それを黄金比や白銀比のようにすでに確立されているものからもってくると、満足する結果にたどりつきやすいのではないかと思うのです。
<2>黄金比
19世紀には、黄金比がいたるところで探し求められました。探検家や冒険家が遺跡や宝物、新しい航路や大陸を探すように、「あれここも黄金比だぞ!」「これもそうかもしれない」などと言っていたのかもしれません。
黄金比はどこに隠れているのでしょうか。例えばパルテノン神殿やピラミッドなどの建築物に黄金比が潜んでいるというのは有名な話で、ネットで検索しても多くヒットします。ただ、「こじつけなんじゃない?」という書き込みもたくさん出てきます。
確かに、パルテノン神殿は上の方が壊れていますし、一概にピラミッドといってもエジプトには100基以上のピラミッドが存在し、形状も大きさも様々です。その中には底辺と高さの比が黄金比に近いものもありますが、「ピラミッドは黄金比で建てられている!」とは断言するのはちょっと難しいようですね。
身のまわりではクレジットカードや名刺などのカード類、有名企業のロゴなど黄金比を採り入れています。これらもピッタリ1:1.618ではありませんが1:1.6前後の比率が使われているようです。では1:1.618の比率を図形として見てみましょう。
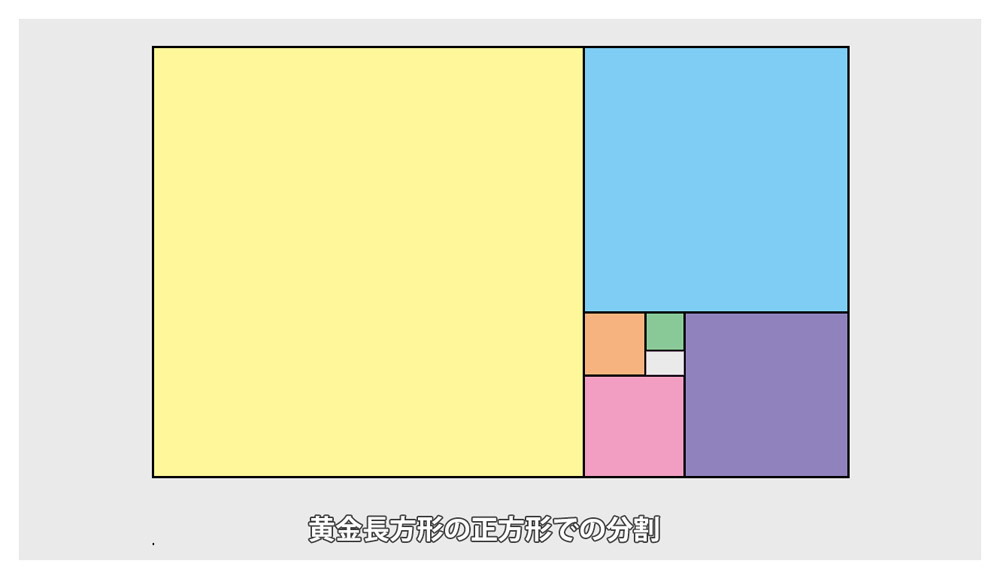
こちらの図のように、短い方の辺を一辺とする正方形を切り取ると、残る長方形も、元の長方形と同じ形の長方形になるものを「黄金長方形」といいます。この正方形の中に、一辺を半径とする円を描いていくと......。
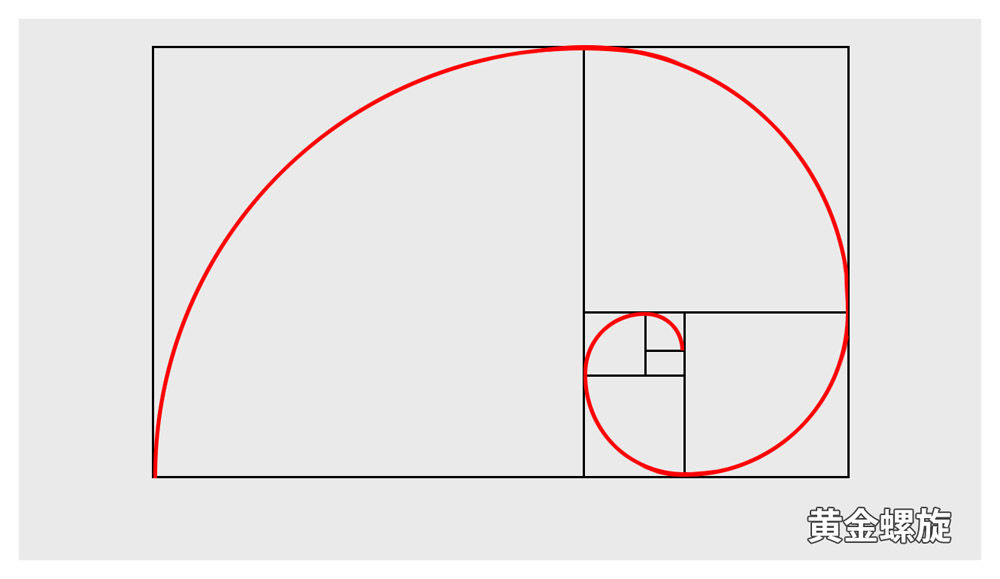
このような図形になります。これは「黄金螺旋」といいオウムガイの形状やヒマワリの種の配列に似ていると言われています。黄金比の書籍やサイトでよく見る図形ですね。
[[SplitPage]]<3>白銀比
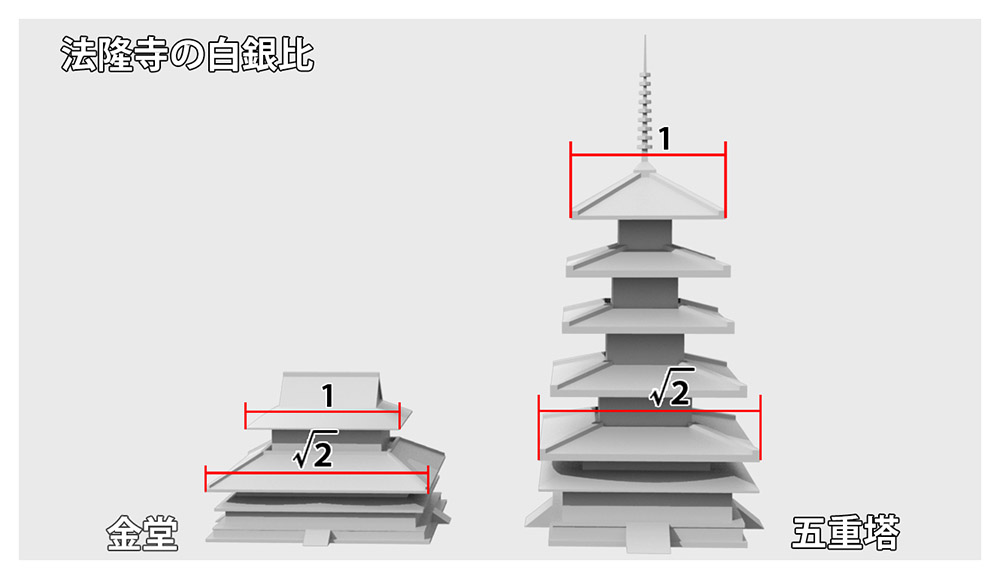
次は「白銀比」です。「白銀比」はお寺など日本の建築物によく見られます。筆者は奈良県出身で、小学生のころ鹿からお弁当を守りながら写生会で法隆寺の五重塔の絵を描きました。この法隆寺の金堂や五重塔の屋根の比率が1:√2になるそうです。
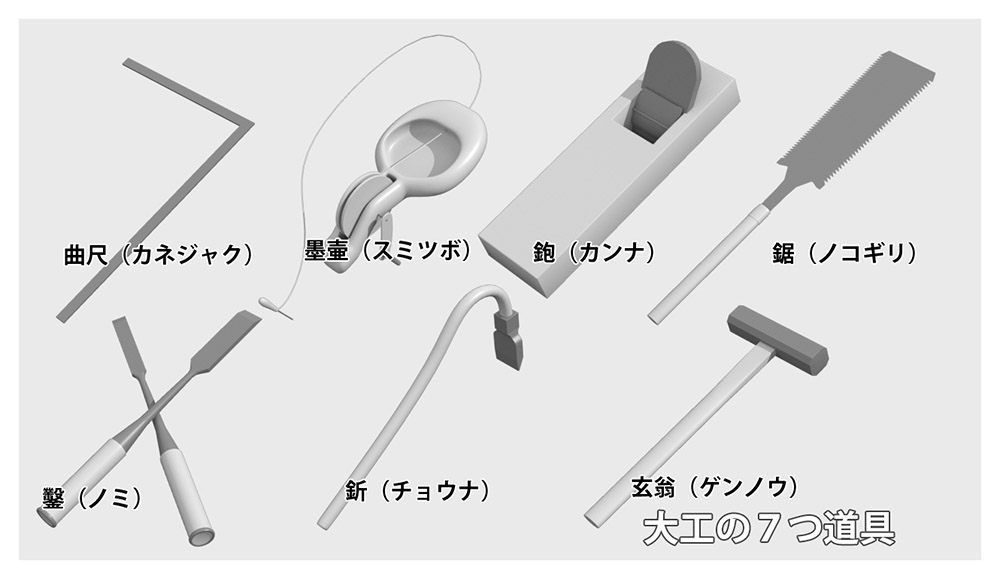
日本ではこの「白銀比」が古くから使われてきました。ここで大工さんの7つ道具を紹介します。実はこの中に白銀比が隠されています。どれかわかりますか?
「曲尺(カネジャク)」:直角を図ったりする定規ですね。
「墨壷(スミツボ)」:墨に浸した糸を伸ばしてピンと張り、糸を指ではじいて直線を引く道具です。
「鉋(カンナ)」:木材の表面を削って平らにする道具。
「鋸(ノコギリ)」:木材を切る道具。
「鑿(ノミ)」:木材に穴を空けたり、彫刻をしたりする道具。
「釿(チョウナ)」:筆者も使ったことがないですが、これは丸太の皮をはいだり、木材の荒削りをするための道具です。
「玄翁(ゲンノウ)」:いわゆるトンカチですね。ノミを叩いたり、釘を打ったりする道具。
答えは、左上の曲尺です!
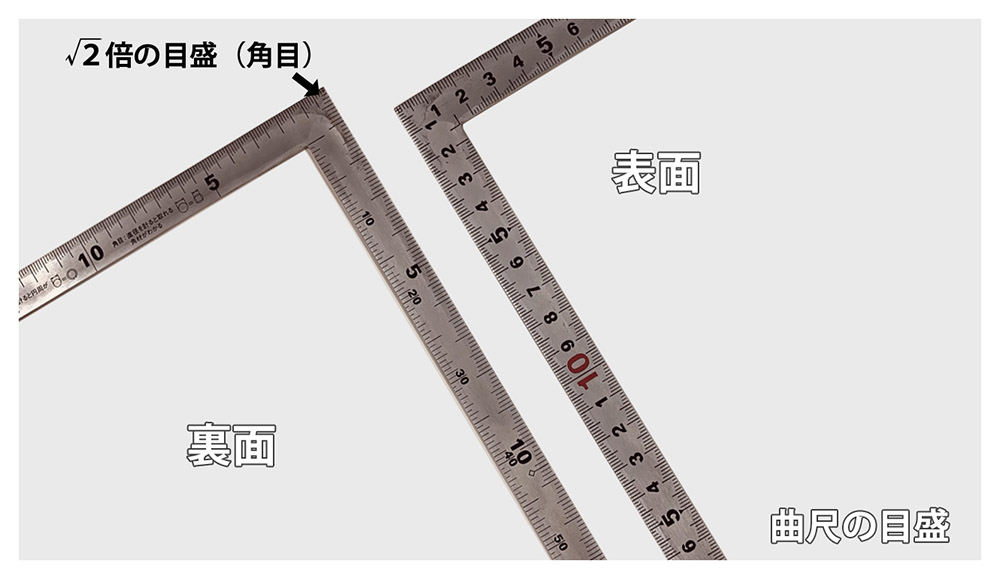
曲尺にはいろいろな目盛がついています。表面には「表目盛」といって長さを図るための目盛、裏面には「角目」と「丸目」という目盛がついており、この「角目」というのが実際のサイズの√2倍の目盛なのです。
では、どういうときに使用するかというと、
①丸太の外周に、曲尺の直角になっている角Cが接するように当てます。曲尺の短い方と長い方が丸太の外周に接しているAとBを結んだ線を引きます。これがこの丸太の直径になります。
②直径を曲尺の「角目」で測ります。「角目」は√2倍の間隔で目盛がついていますので、角目の目盛を読めば、この丸太からとれる正方形の一辺の長さがわかります。角目で測った丸太の直径が水色の直角2等辺三角形ですので、それぞれの辺の対比は1:1:√2になるためです。曲尺には法隆寺が建立された奈良時代には普及していたと言われています。ちなみにもうひとつの目盛の「丸目」には3.14倍の目盛がついています。直径を測れば、簡単に円周がわかるということです。
「丸目」の伝来時期はわかりませんでしたが、「角目」は奈良時代には中国から伝わっていたようです。大工さんは奈良時代から√を操っていたわけですね!
身近な「白銀比」といえば、画用紙やコピー用紙、ノートなどが1:√2の比率でつくられています。用紙はA0やB0を一番大きいサイズとして、数字が増えるにつれ小さくなっていきます。面積が1㎡になる白銀長方形(914mm×1,292mm)がA0でその半分がA1、さらにその半分がA2...となります。半分に折っても元の形状と同じ形状になるのですね。A判はもともとドイツの規格で、現在では国際規格サイズとなっています。
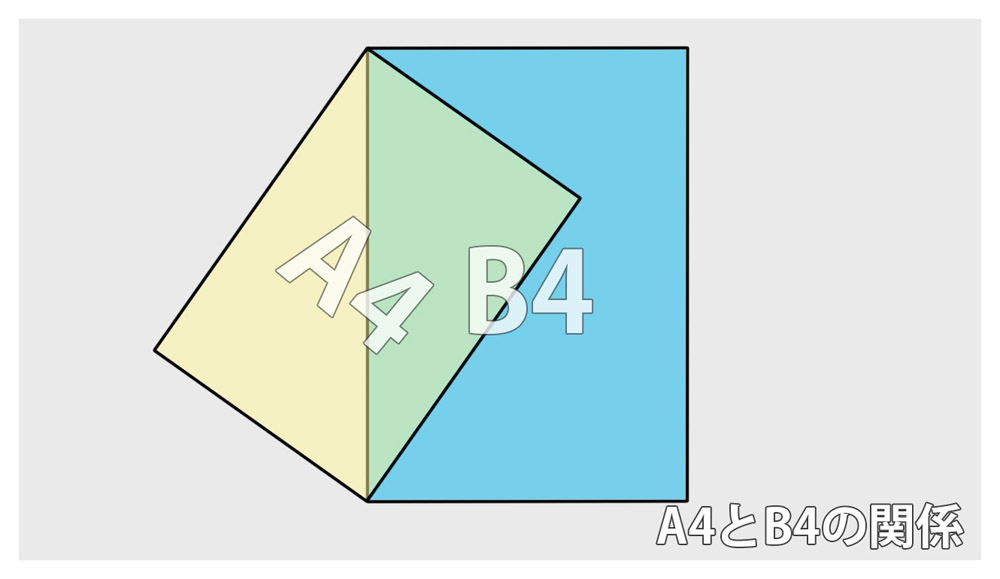
もうひとつのB判は国内規格で面積が1.5㎡になる白銀長方形(1,030mm×1,456mm)をB0とし、その半分がB1、さらにその半分がB2...となります。それではA判とB判はどういった関係にあるのでしょうか? A4とB4の紙を用意して重ねてみると......。
A4の対角線とB4の長辺がピッタリ重なります! 計算されていますね。他にも黄金三角形や正五角形など黄金比が隠されている図形はいろいろあるのですが、今回はこのくらいで「黄金比・白銀比のはなし」は終わりにしたいと思います。
筆者が黄金比を意識するようになったきっかけは、美大受験のために通っていた塾の授業でした。有名な絵画の中に隠されている黄金比や正方形を探し出して、自分の描く絵の構図の参考にしなさいという内容でした。
例えば、自画像を描くにしてもキャンバスいっぱいに描くだけではなく、構図を意識して意図した配置や余白をつくれば、その絵には作者の意思が生まれ、見る人が受ける印象も変わるのだというようなことです。当時は「なるほどな」とは思いましたが、実践はできていなかったと思います。何となく収まりがいいように配置するだけでした。
皆さんもモデリングするときに黄金比や白銀比をこっそりしのばせると、つくりやすく、より良いものができるかもしれません。ぜひ試してみて下さい。
次回は「シワはひし形のはなし」ということで、三浦公亮・東京大学名誉教授が考案した「ミウラ折り」などを例に、シワのでき方や形についておはなししたいと思います。それでは、次回もよろしくお願いいたします。
参考文献
書籍
「デザインの自然学-自然・芸術・建築におけるプロポーション」(ジョージ・ドーチ著、多木浩二・訳、青土社)
「黄金分割―自然と数理と芸術と―」(アルプレヒト・ボイテルスパッヒャー 、ベルンハルト・ペトリ 著、柳井 浩・訳、共立出版)
「法隆寺にひそむ白銀比 五稜郭にひそむ黄金比」(江藤邦彦・著、ベレ出版)
Profile.
大島夏雄/Natsuo Oshima(コロビト)株式会社コロビト 代表取締役、リードモデラー
奈良県出身。多摩美術大学(絵画学科 油画専攻)を卒業後、数社のCG制作会社に所属しモデリングチーフを務める。その後、フリーとなり2009年7月2日に株式会社コロビトを設立。ゲーム、映画、アニメ、CMなど様々なジャンルの仕事を手がける
colobito.com