こんにちは。ビジュアルデベロップメントアーティスト(Visual Development Artist)の伊藤頼子です。連載 第5回、第6回、第7回では透視図法(Perspective)について学びました。今回は黄金比(Golden Ratio)について解説していきます。また、補足として白銀比(Silver Ratio)にも言及します。これらは、画面のレイアウトに加え、ロゴやキャラクターのデザインにも使われる美しく調和のとれた比率です。

伊藤頼子氏(ビジュアルデベロップメントアーティスト)
三重県出身。短大の英文科を卒業後、サンフランシスコのAcademy of Art Universityに留学し、イラストレーションを専攻。卒業後は子供向け絵本のイラストレーション制作に携わる。ゲーム会社でのBackground Designer/Painterを経て、1997年からDreamWorks AnimationにてEnvironmental Design(環境デザイン)やBackground Paint(背景画)を担当。2002年以降はVisual Development Artistに転向し、『Madagascar』(2005)でAnnie Award(アニー賞)にノミネートされる。2013年以降はフリーランスとなり、映画やゲームをはじめ、様々な分野の映像制作に携わる。2013年からはAcademy of Art UniversityのVisual Development Departmentにて後進の育成にも従事。2017年以降は拠点をロサンゼルスに移し、Sony Pictures Animationにて映画制作に携わる。
www.yorikoito.com
躍動感やダイナミズムを象徴する、黄金比の螺旋
連載 第3回では、レイアウトデザインの基本法則の1つとして、三分割法を紹介しました。これと同様に、黄金比もレイアウトデザインに活用できます。黄金比は、デザインの世界において、美しく調和(バランス)のとれた比率を表現するための方法です。黄金比を使って描かれた螺旋は、外へ広がる躍動感、ダイナミズムを象徴します。
下記が、黄金比の定義です。
a : b = b : (a + b) = 1 : 1.618......
短辺 : 長辺= 1 : 1.618 の長方形を、黄金長方形、または黄金矩形(おうごんくけい)と呼びます。
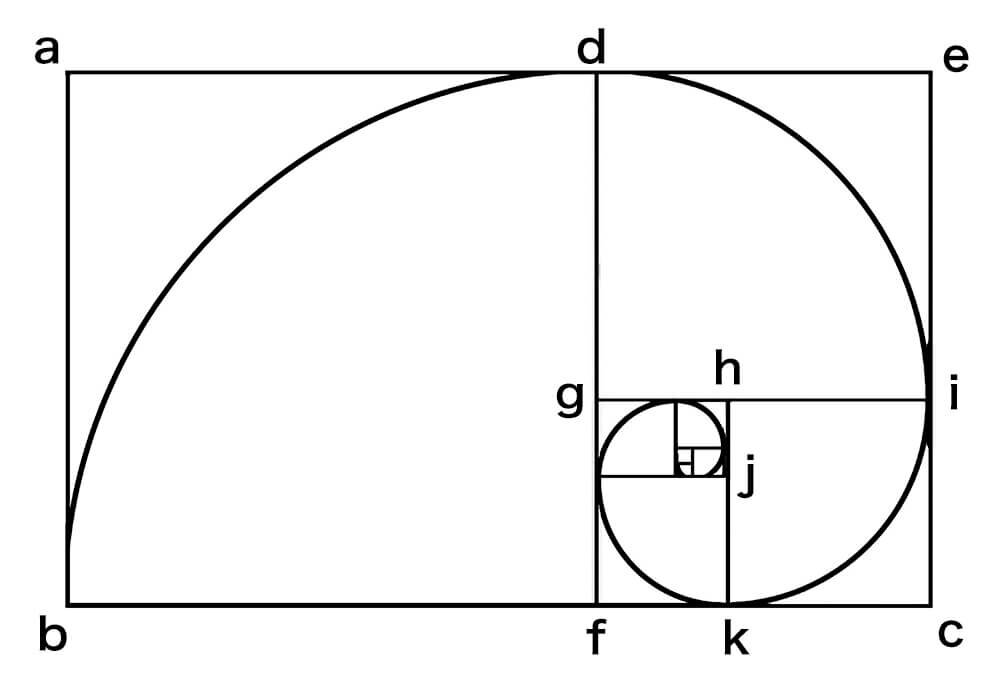
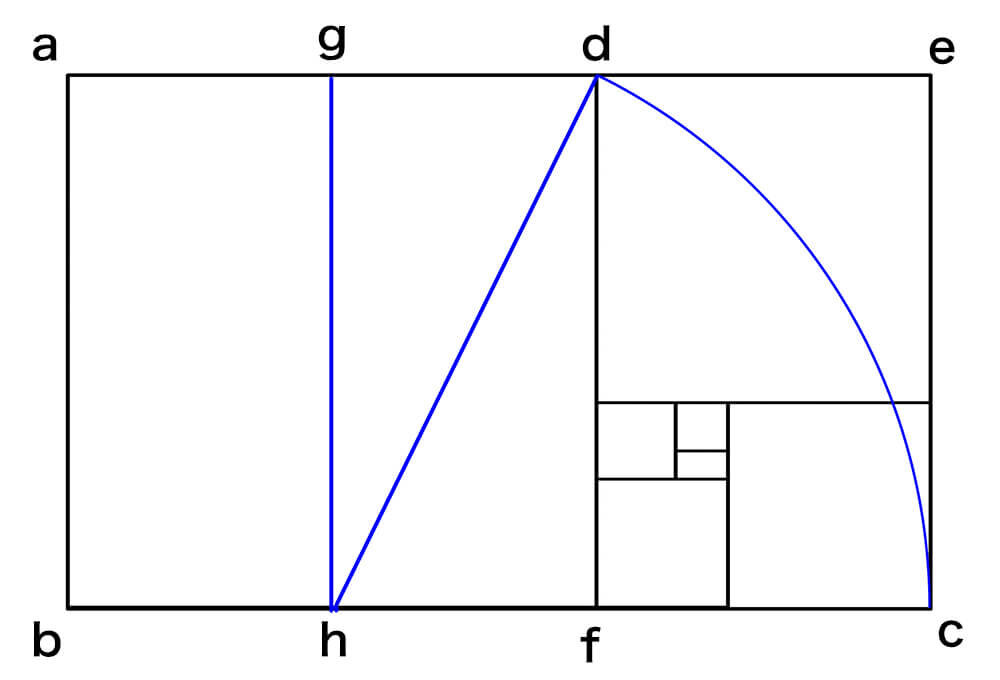
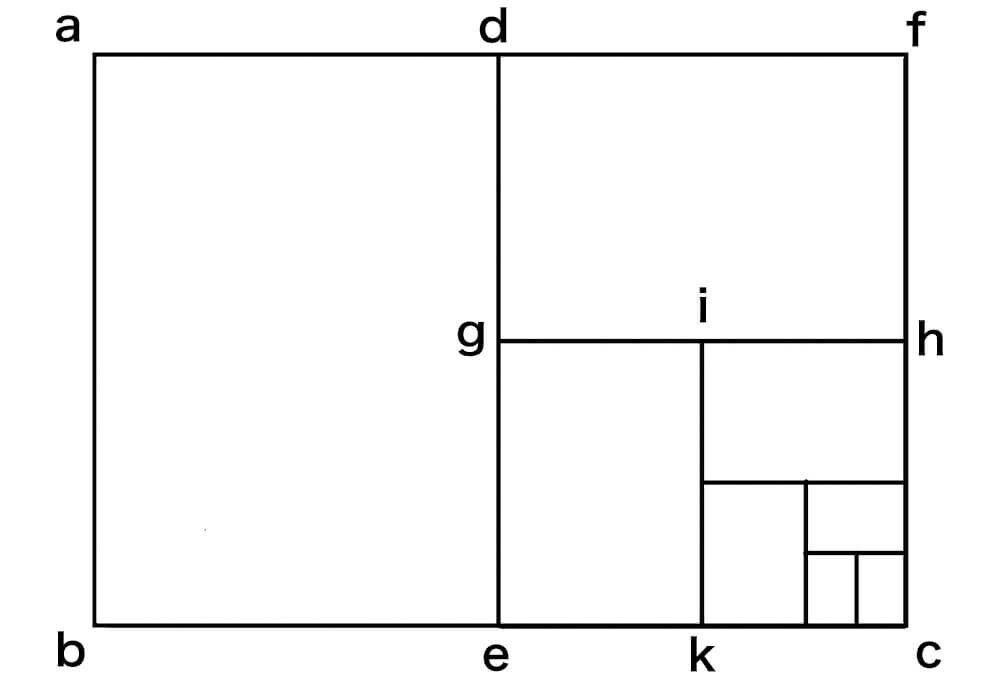
1. 正方形 (abfd) を二等分する辺 (gh) を描く
2. 対角線 (hd) を半径とする円弧と、辺 (bf) の延長線の交点を、点 (c) とする
3. 点 (c) から垂直に伸びる辺と、辺 (ad) の延長線の交点を、点 (e) とする
黄金比は、人体、動物、昆虫、植物などの自然界の中に、数多く発見できます。


さらに黄金比は、グラフィックデザインやロゴデザイン、建築、絵画にも使われています。例えばアップル社のロゴマークや、ペプシコーラで知られるペプシコ社のロゴマークには、黄金比に従った円や曲線が活用されています。エジプトのギザにある三大ピラミッド(紀元前2500年頃)、レオナルド・ダ・ヴィンチの『モナ・リザ』(1500年代前半)の中にも黄金比が発見できると言われています。
映像制作では、黄金長方形を使ったファイグリッド(Phi Grid)が非常によく使われています。

実際のところ、私たちアーティストは、常にきっちりと黄金比に従って作品を設計しているわけではありません。ただし、黄金比は自然界の様々な場所に存在しており、それらを日常的に見ている私たちは、美しく調和のとれた比率であることを実感しています。そのため、生み出される作品の中に、自然と黄金比が使われているのだと思います。
黄金比や、これまでに紹介した法則を理解し、「人は何を美しいと感じるのか」を判断できるセンスを磨くことが一番大切です。法則を理解すれば、それを崩したり、破ったりしても、バランスのとれた構図を生み出せるようになります。
Lesson12:黄金比の螺旋を使い、調和のとれた画を描く
黄金比の螺旋の中心に、画のFocal Pointとなるモチーフを配置してみましょう。

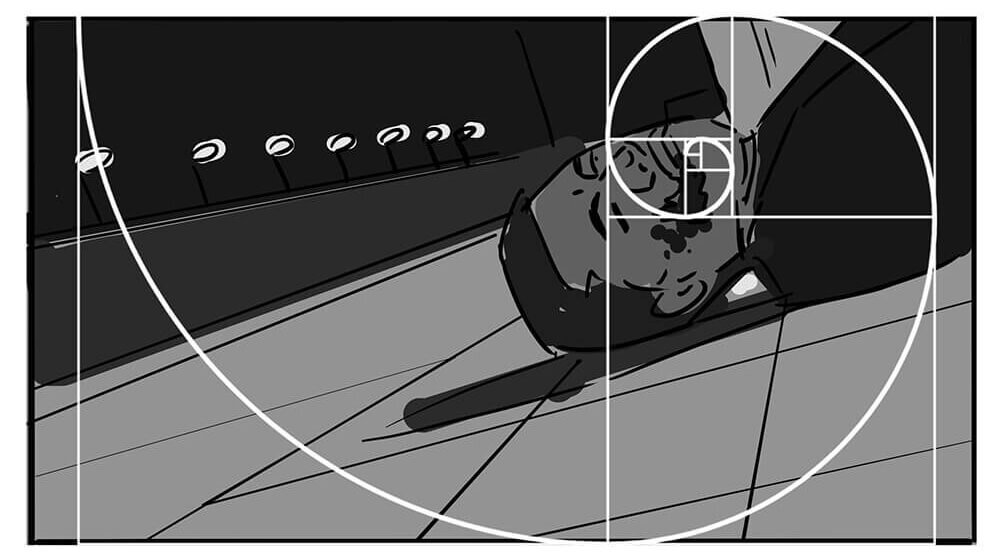
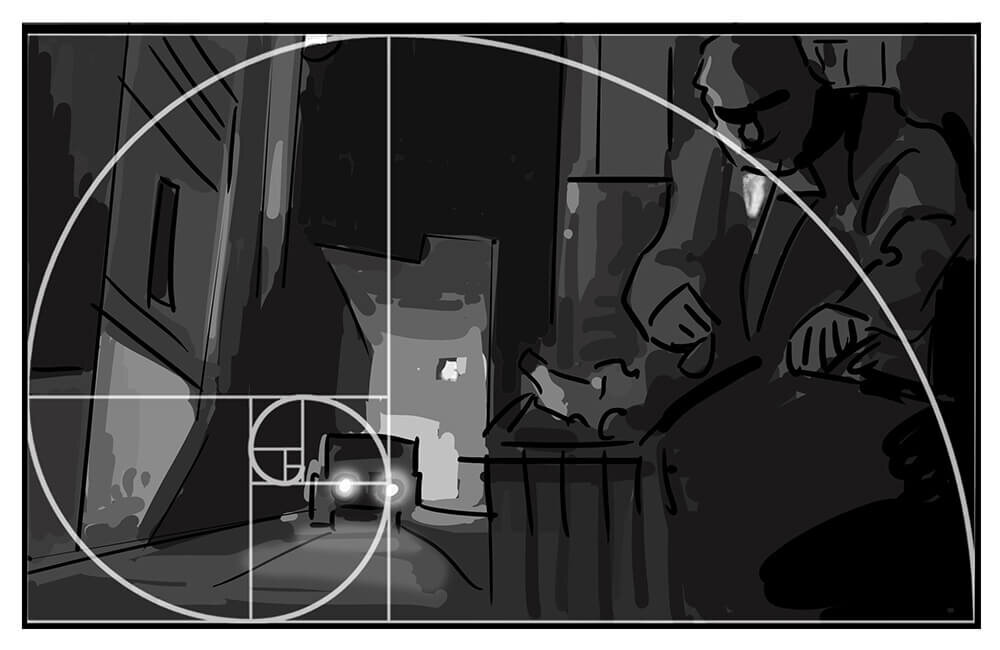
名画のショットを通して、黄金比を学ぶ
名画のショットに、黄金比の螺旋を適用してみましょう。

日本で多用されている白銀比(大和比)
日本のデザインで一般的に使われている白銀比についても、簡単に説明しましょう。白銀比は、大和比とも呼ばれています。
下記が、白銀比の定義です。
1 : √2 = 1 : 1.414......
白銀長方形は何度二等分しても白銀比となるため、無駄がなく合理的です。
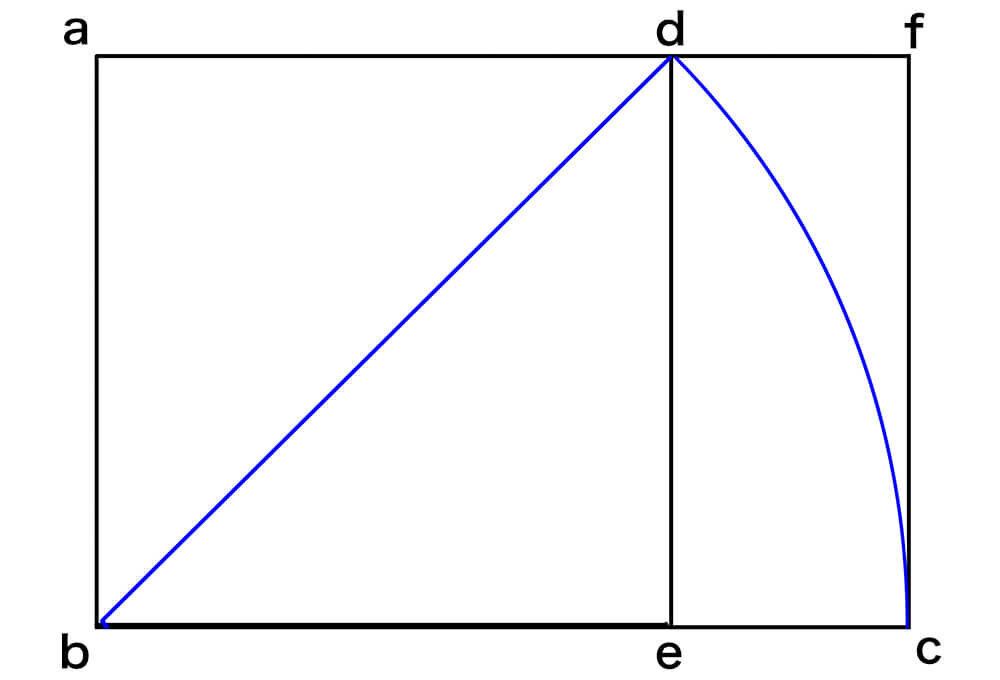
1. 正方形 (abed) の対角線 (bd) を描く
2. 対角線 (bd) を半径とする円弧と、辺 (be) の延長線の交点を、点 (c) とする
3. 点 (c) から垂直に伸びる辺と、辺 (ad) の延長線の交点を、点 (f) とする
日本でお馴染みの「A判」「B判」と呼ばれる紙の比率は白銀比に則っています。法隆寺(607年)など、昔の建築物にも使われています。
ハローキティ、ドラえもん、トトロなど、日本の人気キャラクターの多くにも白銀比が使われています。白銀長方形は、黄金長方形よりも正方形に近い(長辺と短辺の差が小さい)ため、丸みを帯びた可愛い印象になります。日本では古来から白銀比が使われてきたため、この比率が基本となり、数多くの可愛いキャラクターが生み出されてきたのでしょう。
今回のレッスンは以上です。第9回も、ぜひお付き合いください。
TEXT&ARTWORK_伊藤頼子
EDIT_尾形美幸(CGWORLD)
PHOTO_弘田充